Рассмотрим произведение конечного числа линейных биномов 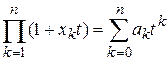 . В правой части равенства коэффициенты имеют вид
. В правой части равенства коэффициенты имеют вид 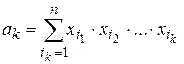 .
.
Определение. Производящей функцией последовательности 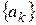 называется сумма степенного ряда
называется сумма степенного ряда 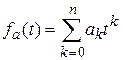 .
.
Идея метода производящих функций такова: необходимо вычислить все члены некоторой последовательности 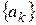 . С помощью рекуррентного соотношения для
. С помощью рекуррентного соотношения для 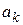 из некоторых комбинаторных соображений вычисляют производящую функцию
из некоторых комбинаторных соображений вычисляют производящую функцию 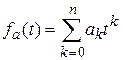 . Раскладывая затем
. Раскладывая затем 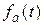 в ряд и находя коэффициенты при tk, тем самым находят
в ряд и находя коэффициенты при tk, тем самым находят 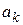 .
.
Пример 1. Из формулы бинома Ньютона 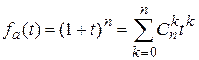 , последовательность биноминальных коэффициентов имеет производящую функцию
, последовательность биноминальных коэффициентов имеет производящую функцию 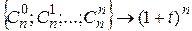 (1)
(1)
Пример 2. Пусть 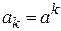 , к=0;1;2;… Тогда
, к=0;1;2;… Тогда 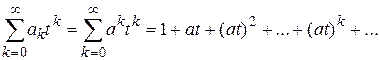 , это бесконечно убывающая геометрическая прогрессия со знаменателем
, это бесконечно убывающая геометрическая прогрессия со знаменателем 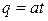 . В этом случае производящая функция имеет вид
. В этом случае производящая функция имеет вид 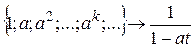 при
при 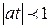 . (2)
. (2)
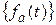 - класс обычных производящих функций
- класс обычных производящих функций 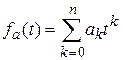
Операции в классе производящих функций:
1. Суммой последовательностей 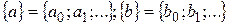 называется последовательность
называется последовательность 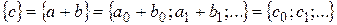 , а суммой производящих функций
, а суммой производящих функций 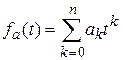 и
и 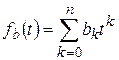 - производящая функция
- производящая функция 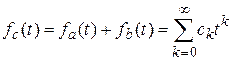 . (3)
. (3)
2. Произведением (сверткой) последовательностей 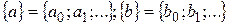 называется последовательность
называется последовательность 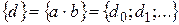 , у которой
, у которой 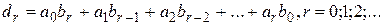 (4)
(4)
|
|
|
а произведением производящих функций 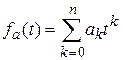 и
и 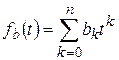 - производящая функция
- производящая функция 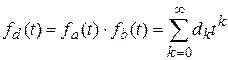 . (5)
. (5)
Нуль в классе производящих функций 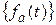 - это
- это 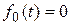 ; ей соответствует нулевая последовательность {0;0;…;0;…}. Единица в классе производящих функций
; ей соответствует нулевая последовательность {0;0;…;0;…}. Единица в классе производящих функций 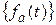 - это
- это 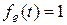 ; ей соответствует единичная последовательность {1;0;0;…;0;…}=e. Обратный относительно сложения (противоположный) элемент в классе производящих функций есть следующая функция:
; ей соответствует единичная последовательность {1;0;0;…;0;…}=e. Обратный относительно сложения (противоположный) элемент в классе производящих функций есть следующая функция: 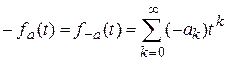 , которой соответствует последовательность {-a0;-a1;…;-ak;…}. Обратный элемент относительно умножения в классе производящих функций есть функция
, которой соответствует последовательность {-a0;-a1;…;-ak;…}. Обратный элемент относительно умножения в классе производящих функций есть функция 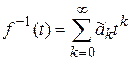 , причем
, причем 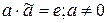 . Т.к.
. Т.к. 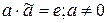 ,
, 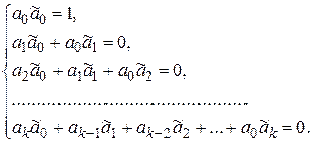
Умножение производящей функции на действительное число 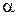 определяется по формуле
определяется по формуле 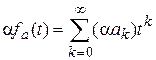 . (6)
. (6)
 2014-02-09
2014-02-09 2628
2628








