Поиск экстремальных путей и контуров

Лк. 8. Методология постановки и анализа типовых задач информационной логистики

8.1.1. Задача о кратчайшем пути. Пусть задана сеть из n + 1 вершины, то есть ориентированный граф, в котором выделены две вершины - вход (нулевая вершина) и выход (вершина с номером n). Для каждой дуги заданы числа, называемые длинами дуг. Длиной пути {контура) называется сумма длин входящих в него дуг (если длины дуг не заданы, то длина пути (контура) определяется как число входящих в него дуг). Задача заключается в поиске кратчайшего пути (пути минимальной длины) от входа до выхода сети.

Известно, что для существования кратчайшего пути необходимо и достаточно отсутствия в сети контуров отрицательной длины.

Кратчайший путь в сети определяется следующим алгоритмом.

Алгоритм 1.

Для любого графа всегда можно пронумеровать вершины таким образом, что для любой дуги (i,j) имеет место j > i. Такая нумерация называется правильной. Легко показать, что в сети без контуров всегда существует правильная нумерация. Обозначим l - длину дуги (i;j). Кратчайший путь в сети, имеющей правильную нумерацию, определяется следующим алгоритмом.

Шаг 0: Помечаем нулевую вершину индексом λ₀ = 0;

Шаг k_: помечаем вершину k индексом λ _k = min (λ _i + l_ik).

i<k

Индекс выхода λ_n будет равен длине кратчайшего пути. На рисунке 8.1 приведен пример применения алгоритма 1 для определения кратчайшего пути (числа у дуг равны длинам дуг, индексы вершин помещены в квадратные скобки, кратчайший путь выделен двойными линиями).

Когда индексы (называемые в некоторых задачах потенциалами вершин) установятся, кратчайший путь определяется методом обратного хода от выхода к входу/

Алгоритм 2 (алгоритм Форда).

Шаг 0: Помечаем нулевую вершину индексом λ₀ = 0, все остальные вершины индексами λ_i⁰ = 1,n;

Шаг k_: Рассматриваем все дуги. Если для дуги (i;j) λ_j^k-1-λ_i^k-1>l_ij, то вычисляем новое значение λ_j^k= λ_j^k-1+l_ij.

Индексы устанавливаются за конечное число шагов. Обозначим { λ_i^* } - установившиеся значения индексов, которые обладают следующим свойством: величина А_г равна длине кратчайшего пути из нулевой вершины в вершину i. Кратчайший путь из вершины 0 в вершину i определяется методом обратного хода.

Если длины всех дуг неотрицательны, то для поиска кратчайшего пути применим следующий алгоритм.

Алгоритм 3.

Шаг 0: Помечаем нулевую вершину индексом λ₀ = 0;

Шаг k_: Пусть уже помечено некоторое множество вершин. Обозначим Q - множество непомеченных вершин, смежных с помеченными. Для каждой вершины k Є Q вычисляем величину ξ_k ⁼ min (λ_i+l_ik ), где минимум берется по всем помеченным вершинам i, смежным с вершиной k. Помечаем вершину k, для которой величина ξ_k минимальна, индексом λ_k = ξ_k.

Подобную процедуру повторяем до тех пор, пока не будет помечена вершина n. Длина кратчайшего пути равна λn, а сам кратчайший путь определяется так, как это было описано выше.

Аналогично задаче о кратчайшем пути формулируется и решается задача о максимальном (длиннейшем) пути - достаточно изменить знаки дуг на противоположные и решить задачу о кратчайшем пути. Для существования решения задачи о максимальном пути необходимо и достаточно отсутствия контуров положительной длины.

В задаче поиска пути максимальной надежности длины дуг интерпретируются, например, как вероятности того, что существует связь между соответствующими двумя пунктами. Заменяя длины дуг их логарифмами, взятыми с обратными знаками, получаем, что путь максимальной надежности в исходном графе будет соответствовать кратчайшему пути в новом графе.

Гораздо более сложными (NP-полными¹) являются задачи поиска элементарных путей кратчайшей (максимальной) длины в случае, когда в сети имеются контуры отрицательной (соответственно, положительной) длины². Эффективных (не сводящихся к полному перебору) точных алгоритмов для них не существует.

К таким же сложным задачам относятся и задачи поиска кратчайших или длиннейших путей или контуров, проходящих через все вершины графа (элементарный путь (контур), проходящий через все вершины графа, называется гамилътоновым путем (контуром)). Классическим примером задачи поиска гамильтонова контура является задача коммивояжера, заключающаяся в следующем. Коммивояжер (бродячий торговец) должен посетить n городов, побывав в каждом ровно один раз, и вернуться в исходный пункт своего путешествия. Заданы неотрицательные длины дуг, интерпретируемые как расстояние между городами или стоимости проезда. Требуется найти гамильтонов контур минимальной длины (в графе из n вершин существует n! гамильтоновых контуров).

Алгоритмы решения задачи о кратчайшем пути позволяют решать в логистике широкий класс задач дискретной оптимизации. В качестве примера приведем задачу целочисленного линейного программирования - задачу о ранце (о рюкзаке), к которой сводятся многие практически важные задачи определения оптимальной комбинации факторов при ограничениях на общий вес, площадь, объем, финансирование и т.д.

Задача о ранце. Пусть имеется n предметов, которые могут быть полезны в походе. Полезность г-го предмета оценивается числом а_i, вес предмета (или его объем) - b_i. Суммарный вес, который может нести турист (объем рюкзака), ограничен величиной R. Требуется найти набор предметов, обладающий максимальной суммарной полезностью и удовлетворяющий ограничению.

Обозначим x_i, - переменную, принимающую значение ноль (если i-ый предмет не кладется в ранец) или единица (если i-ый предмет кладется в ранец). Тогда задача о ранце имеет вид:

(*)

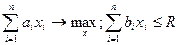Верхняя оценка числа возможных комбинаций – 2ⁿ. Однако для решения задачи о ранце существует эффективный алгоритм - метод динамического программирования. При его использовании строится сеть (см. примеры в «Вагнер Г. Основы исследования операций. М. Мир, 1972») по следующим правилам. По оси абсцисс будем последовательно откладывать номера предметов, по оси ординат - их вес. Из каждой точки (начиная с точки (0; 0)) выходят две дуги - горизонтальная (соответствующая альтернативе «не брать предмет») и наклонная (соответствующая альтернативе «взять предмет»), вертикальная проекция которой равна весу предмета. Длины наклонных дуг положим равными ценности предметов, длины горизонтальных дуг - нулю. Полученная сеть (конечная вершина является фиктивной и вес любой дуги, соединяющей ее с другими вершинами, равен нулю) обладает следующими свойствами: любому решению задачи (*) соответствует некоторый путь в этой сети; любому пути соответствует некоторое решение задачи. Таким образом, задача свелась к нахождению пути максимальной длины.

8.1.2. Задача поиска контура минимальной длины решается следующим образом. Если известно, что искомый контур содержит некоторую вершину, то нужно определить кратчайшей путь от этой вершины до нее же, применяя описанные выше алгоритмы. Так как в общем случае контур минимальной длины может проходить через любую вершину графа, то находятся контуры минимальной длины, проходящие через каждую вершину, и среди них выбирается кратчайший. Более простым является следующий алгоритм 4: берется первая вершина (в произвольном их упорядочении) графа и рассматривается сеть, в которой эта вершина является одновременно конечной и начальной вершиной. Для этой сети (применением описанного выше алгоритма) ищется путь μ₁ минимальной длины L(μ₁). Затем первая вершина отбрасывается, и минимальный путь μ₂ ищется для сети, в которой начальной и конечной вершиной является вторая вершина. Затем отбрасывается вторая вершина и т.д. для всех вершин исходного графа, для которых существует контур, проходящий через них и через вершины с большими номерами. Контуром минимальной длины будет контур μ_min, длина которого равна L(μ_min) = min {L(μ ₁),…L(μ _n) }.

8.1.3. Задача поиска контура минимальной средней длины заключается в поиске контура, для которого минимально отношение его длины к числу содержащихся в нем дуг. Для решения этой задачи используется алгоритм 5:

1. Определяем произвольный контур. Пусть L - длина этого контура, k-число его дуг. Вычисляем l_cp=L/k и добавляем -l_cp к длинам l_ij всех дуг.

Затем определяем контур отрицательной длины, повторяем шаг 1, и т.д. до тех пор, пока на очередном шаге таких контуров не найдется.

Так как на каждом шаге длины всех дуг изменялись на одно и то же число, то на последнем шаге длина дуги равна lij- ц, где ц - суммарное изменение длины каждой дуги на всех шагах.

Значение ц равно минимальной средней длине дуг контуров графа. При этом контуром минимальной средней длины является контур, определенный на предпоследнем шаге.

8.1.4. Путь максимальной эффективности. Пусть задана сеть, в которой для каждой дуги (i;j) определены два числа (Э,S), интерпретируемые как эффект при осуществлении соответствующей операции - Э и затраты на эту операцию - S. Эффективность K(μ) пути μ определяется как отношение его эффекта к затратам. Задача заключается в поиске пути μ^* максимальной эффективности: К(μ) —> max.

Если решение K* = K(μ^*) этой задачи известно, то по определению К выполнено: Э(μ)-K^*S(μ)≤0 (**) V Следовательно, задача свелась к поиску минимального значения К, для которого имеет место (**). Другими словами, необходимо найти минимальное К, такое, что все пути (длина которых определяется как l_ij(K*) = Э_ij - K* S_ij) в сети имеют неположительную длину (неравенство (**) должно выполняться, в том числе, и для пути максимальной длины).

Алгоритм 6. 1) Положим К = 0. Находим путь μ₁ максимальной длины. Положим K₁ = Э(μ₁) / S(μ₁) (заметим, что при K = K₁ длина пути μ(K₁) равна нулю).

2) Находим максимальный путь μ₂ при K = K₁. Если длина пути μ.₂, которую мы обозначим L(K₁), равна нулю, то задача решена. Если L(K₁) > 0, то вычисляем K₂ = Э(μ₂) / S(μ₂) и находим максимальный путь μ₂ при K = К₂ ит.д.