Пусть дан характеристический многочлен линейной системы 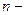 го порядка:
го порядка:
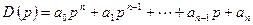 . (4.4)
. (4.4)
Подставив в него 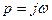 , получим:
, получим: 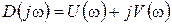 ,
,
где
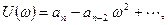
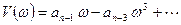 (4.5)
(4.5)
Годограф 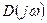 называется кривой Михайлова. Практически кривая Михайлова строится по точкам на комплексной плоскости. Задают несколько разных значений
называется кривой Михайлова. Практически кривая Михайлова строится по точкам на комплексной плоскости. Задают несколько разных значений 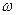 в интервале между
в интервале между  до
до  . По формулам (4.5) вычисляют координаты точек кривой Михайлова, которая может иметь вид, представленный на рис. 4.1.
. По формулам (4.5) вычисляют координаты точек кривой Михайлова, которая может иметь вид, представленный на рис. 4.1.
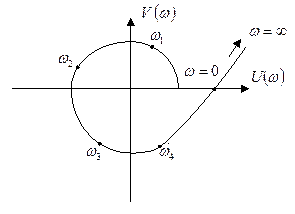
Рис. 4.1
Для различных  кривая Михайлова может иметь примерно такие формы как показано на рис. 4.2.
кривая Михайлова может иметь примерно такие формы как показано на рис. 4.2.
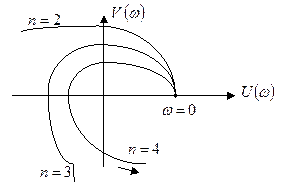
Рис. 4.2
Формулировка критерия. (доказательство см [1]).
Для устойчивости линейной системы 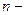 го порядка необходимо и достаточно, чтобы изменение аргумента функции
го порядка необходимо и достаточно, чтобы изменение аргумента функции 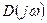 при изменении
при изменении 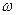 от
от 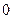 до
до 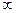 , равнялась бы
, равнялась бы  .
.
Другими словами, требуется, чтобы кривая Михайлова проходила последовательно 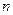 квадрантов против часовой стрелки, окружая начало координат.
квадрантов против часовой стрелки, окружая начало координат.
Граница устойчивости будет иметь место, если кривая Михайлова проходит через начало координат, откуда получаем:
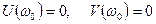 .
.
Эти выражения можно использовать для построения областей устойчивости системы на плоскости любых двух параметров 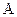 и
и 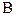 , выбираемых при проектировании системы (это могут быть, например, коэффициент усиления и построения времени). Тогда последние уравнения можно записать в виде:
, выбираемых при проектировании системы (это могут быть, например, коэффициент усиления и построения времени). Тогда последние уравнения можно записать в виде:
|
|
|
 .
.
Путем задания разных значений величины 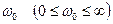 каждый раз из этих уравнений определяются значения параметров
каждый раз из этих уравнений определяются значения параметров 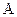 и
и 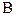 . В результате по точкам строятся границы устойчивости на плоскости
. В результате по точкам строятся границы устойчивости на плоскости 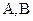 .
.
 2014-02-09
2014-02-09 438
438








