Проекций

Характеристические уравнения некоторых геодезических

В теории отображения поверхностей указывается на то, что все многообразие конформных отображений следует из аналитической функции комплексных переменных, связывающей изометрические координаты на обеих поверхностях (7. 3, 7. 4, 7. 21). Под изометрическими координатами на любой поверхности понимают такие, когда равным приращениям координат соответствуют равные линейные приращения вдоль координатных линий. Заметим, что в математике такая система координат называется изотермической, а в картографии и геодезии принято название изометрическая. Таким образом, необходимо установить изометрические координаты степени (Dq)^j, которые представляют собой малые убывающие величины при малых Dq. Для Республики Беларусь, например, В₀» 54⁰ и cosB₀ £ 3. 8 ´ 10⁶ м. Если размеры изображаемой в одной зоне области ограничить разностью широт и долгот

(Dq)_max» (DL)_max £ 6⁰» 0.1,

а вычисления координат производить с точностью до 0. 001 м, что соответствует стандартам точности современных измерительных технологий, то в разложениях (7. 33) достаточно ограничиться восьмыми степенями разложений. При этом замечаем, что остаточный член в форме Лагранжа будет

r ₍₉₎ (x, y)» (3.8 ´ 10⁶) (0.1)⁹/9! £ 0.001м.

7. 6. 1. Поперечно – цилиндрические проекции

В поперечно – цилиндрических геодезических проекциях ставится условие, чтобы длина дуги меридиана эллипсоида, принимаемого на плоскости проекции за осевой, изображалась без искажений (в натуральную величину), когда частный масштаб длин вдоль меридиана равен единице (m₀ = 1) – это проекция Гаусса – Крюгера, либо при условии m₀ £ 1= const – универсальная проекция Меркатора, известная как проекция UTM. Отсюда видно, что проекция UTM является обобщением проекции Гаусса – Крюгера.

Здесь можем записать для уравнения из (7. 25)

,

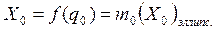где (X₀)_{эллипс .} – длина дуги меридиана эллипсоида, отсчитанная от экватора до средней точки проекции с широтой В₀. И первое уравнение из (7. 26) можем записать в виде

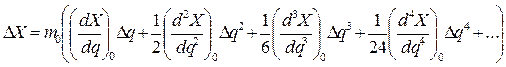. (7. 33)

Производные в этом уравнении получаем следующим образом. Как известно, дифференциал дуги меридиана эллипсоида имеет выражение

,

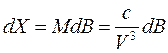откуда можем записать

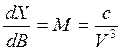
и далее по правилу дифференцирования неявных функций

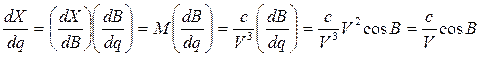(7. 34)

Здесь производную 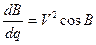получаем из (7. 18). Производная, вычисленная по координатам начальной точки проекции, имеет выражение

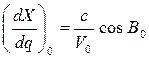
Далее действуем по известным правилам дифференциального исчисления, когда вторая производная вычисляется как производная от первой и т. д. В результате получаем

;

.

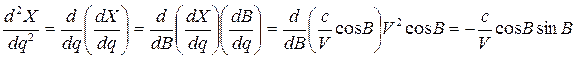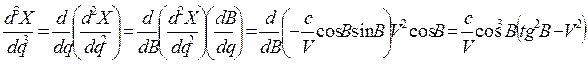Последовательно вычисляем необходимое число производных и, следовательно, коэффициентов разложения (7. 33). При этом заметим, что в этом разложении коэффициенты удовлетворяют условию .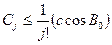

Действуя указанным ранее образом, вычисляем необходимое число производных и в результате получаем следующие выражения коэффициентов первого характеристического уравнения из (7. 26) для поперечно – цилиндрических проекций:

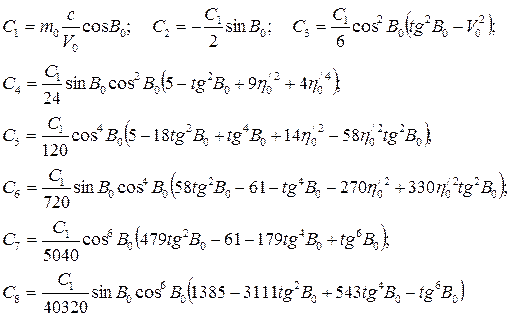(7. 35)

Здесь используем ранее принятое обозначение h₀ ^/2 = e^/2cos²B₀, а в коэффициентах C₅ и С₆ по малости отброшены слагаемые с множителем h₀ ^/4, а в коэффициентах С₇ и С₈ – с множителем h₀ ^/2.

Полагая значение m₀ = 1, получаем проекцию Гаусса – Крюгера, а при m₀ = 0. 9996 – проекцию UTM. Вообще говоря, варьируя значением m₀, можно управлять распределением искажений длин в пределах изображаемой области. О том, как это делается, мы остановимся позднее.

Поперечно-цилиндрические проекции наиболее удобны для изображения на плоскости областей эллипсоида, вытянутых вдоль меридиана.