Канонический вид гиперболических, параболических
При помощи общих интегралов определяются новые переменные и, поэтому форма записи уравнения в новых переменных будет зависеть от дискриминанта 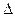 . Рассмотрим все возможные случаи
. Рассмотрим все возможные случаи 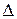 .
.
1) Дискриминант 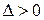 в области
в области 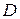 . Гиперболический тип уравнения. В этом случае правые части уравнений (10) будут действительными и различными функциями. Решая эти дифференциальные уравнения найдем два общих интеграла
. Гиперболический тип уравнения. В этом случае правые части уравнений (10) будут действительными и различными функциями. Решая эти дифференциальные уравнения найдем два общих интеграла 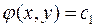 и
и 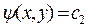 . Тогда, согласно доказанному выше, полагая в качестве новых переменных
. Тогда, согласно доказанному выше, полагая в качестве новых переменных 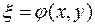 ,
, 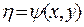 , получим
, получим 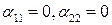 и в новых переменных исходное уравнение будет иметь следующий вид
и в новых переменных исходное уравнение будет иметь следующий вид 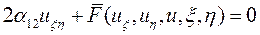 .
.
Преобразуя, получим
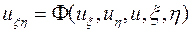 ,
, 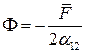 .
.
Это и есть каноническая форма гиперболического уравнения. Приведем еще одну каноническую форму для гиперболических уравнений. Для этого введем новые переменные
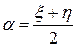 ,
, 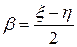 .
.
Вычислим частные производные
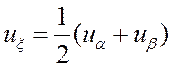 ,
, 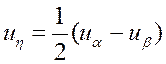
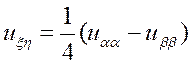 .
.
Подставляя эти выражения в первую каноническую форму, получим
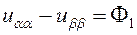 ,
, 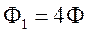
Это вторая каноническая форма для гиперболических уравнений.
2) Дискриминант 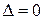 в области
в области 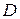 . Параболический тип уравнений. В этом случае решения уравнений (10) совпадают и в результате решения этих уравнений получим только один общий интеграл
. Параболический тип уравнений. В этом случае решения уравнений (10) совпадают и в результате решения этих уравнений получим только один общий интеграл 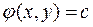 . Возьмем в качестве новой переменной
. Возьмем в качестве новой переменной 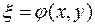 . В качестве второй переменной возьмем любую функцию
. В качестве второй переменной возьмем любую функцию 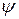 , функционально не зависящую от
, функционально не зависящую от 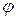 , то есть такую, что
, то есть такую, что
|
|
|
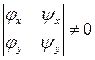 .
.
При таком выборе получим
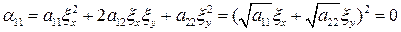 .
.
При этом 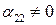 в силу произвольности
в силу произвольности 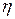 . Кроме того,
. Кроме того,
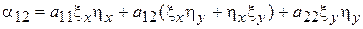 =
=
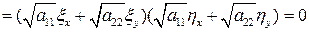 .
.
Учитывая это, получим
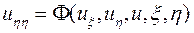 ,
, 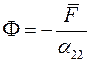 .
.
Получили каноническую форму для параболических уравнений.
3) Пусть дискриминант 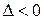 в области
в области 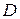 . Эллиптический тип уравнений. В этом случае правые части уравнений (10) будут комплексными функциями. Тогда общий интеграл также будет комплексной функцией. Обозначим эту функцию через
. Эллиптический тип уравнений. В этом случае правые части уравнений (10) будут комплексными функциями. Тогда общий интеграл также будет комплексной функцией. Обозначим эту функцию через 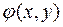 . Сопряженная к ней
. Сопряженная к ней 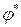 также будет общим интегралом. Тогда можно ввести новые комплексные переменные
также будет общим интегралом. Тогда можно ввести новые комплексные переменные
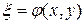 ,
, 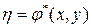 .
.
В результате введения этих переменных, как и в случае гиперболических уравнений, получим 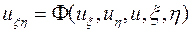 - канонический вид эллиптических уравнений. Рассмотрим также и другую каноническую форму с вещественными переменными. Для этого введем новые, вещественные переменные
- канонический вид эллиптических уравнений. Рассмотрим также и другую каноническую форму с вещественными переменными. Для этого введем новые, вещественные переменные
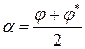 ,
, 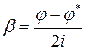 .
.
Откуда получим 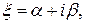
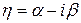 . Вычисляя коэффициенты по формулам (6) получим вторую каноническую форму для эллиптических уравнений
. Вычисляя коэффициенты по формулам (6) получим вторую каноническую форму для эллиптических уравнений
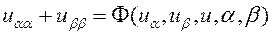 .
.
Пример 1. Уравнение в частных производных 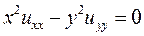 , заданное в области
, заданное в области 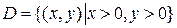 , преобразовать к каноническому виду.
, преобразовать к каноническому виду.
Решение. Вычислим дискриминант данного уравнения
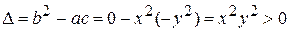 .
.
Следовательно, данное уравнение гиперболического типа. Составим характеристическое уравнение 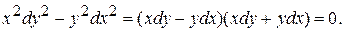
Откуда получим 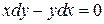 ,
, 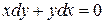 . Решим эти дифференциальные уравнения методом разделения переменных:
. Решим эти дифференциальные уравнения методом разделения переменных:
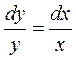
Откуда, интегрируя, получим 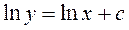 или
или 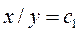 . Аналогично решим второе уравнение
. Аналогично решим второе уравнение
|
|
|
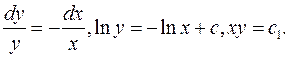
Таким образом, общие интегралы будут такими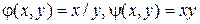 . Введем, согласно общей теории преобразований, новые переменные
. Введем, согласно общей теории преобразований, новые переменные
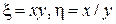 .
.
По формулам (5) для частных производных 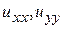 найдем выражения в новых переменных:
найдем выражения в новых переменных:
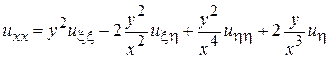
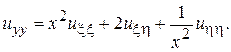
Подставляя эти выражения в исходное уравнение, получим канонический вид в новых переменных:

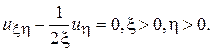
Пример 2. Преобразовать в канонический вид уравнение
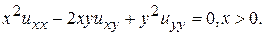
Решение. Вычислим дискриминант 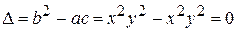 . Дискриминант равен нулю и, следовательно, уравнение параболическое. Составим характеристическое уравнение:
. Дискриминант равен нулю и, следовательно, уравнение параболическое. Составим характеристическое уравнение:
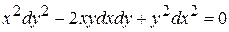 или
или 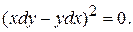
Откуда 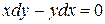 и общий интеграл этого уравнения будет
и общий интеграл этого уравнения будет
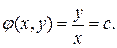
Введем новые переменные 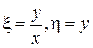 и найдем выражения для частных производных в новых переменных
и найдем выражения для частных производных в новых переменных
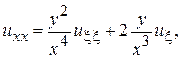
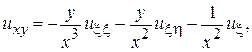
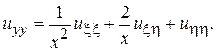
Подставляя в исходное уравнение эти выражения, получим 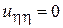 - канонический вид исходного уравнения.
- канонический вид исходного уравнения.
Пример 3. Преобразовать в канонический вид уравнение
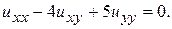
Решение. Вычислим дискриминант 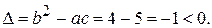 Следовательно, уравнение эллиптическое. Составим характеристическое уравнение
Следовательно, уравнение эллиптическое. Составим характеристическое уравнение 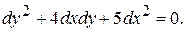 Решая это уравнение, получим
Решая это уравнение, получим
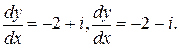
Откуда 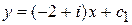 ,
, 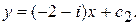 Тогда общими интегралами будут
Тогда общими интегралами будут
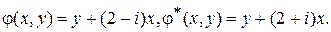
Обозначим через 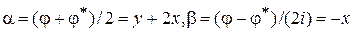 и введем новые переменные
и введем новые переменные 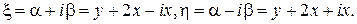 Вычисляя по формулам (5) частные производные и подставляя их в исходное уравнение, получим
Вычисляя по формулам (5) частные производные и подставляя их в исходное уравнение, получим 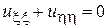 - каноническая форма для исходного уравнения.
- каноническая форма для исходного уравнения.
Пример 4. Уравнение в частных производных 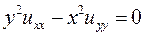 , заданное в области
, заданное в области 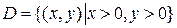 , преобразовать к каноническому виду.
, преобразовать к каноническому виду.
Решение. Вычислим дискриминант 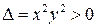 . Следовательно, уравнение является гиперболическим. Составим уравнения характеристик
. Следовательно, уравнение является гиперболическим. Составим уравнения характеристик
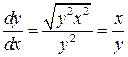 ,
, 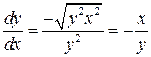 .
.
Решим эти уравнения методом разделения переменных. Преобразуем к виду
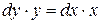 ,
, 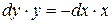 и интегрируя, получим
и интегрируя, получим
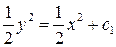 ;
; 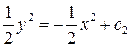 .
.
Следовательно, интегралами будут 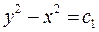 и
и 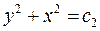 . Новыми переменными в этом случае будут
. Новыми переменными в этом случае будут
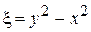 и
и 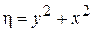 .
.
По формулам (6) вычислим коэффициенты нового уравнения:
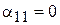 ,
, 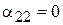 ,
, 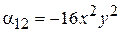 ,
,
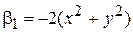 ,
, 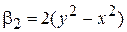 ,
, 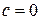 ,
, 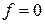 .
.
Подставим их в уравнение (5а) и получим:
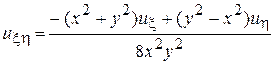 .
.
Выразим x и y через 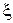 и h и получим канонический вид исходного уравнения
и h и получим канонический вид исходного уравнения
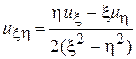 .
.
Пример 5. Уравнение 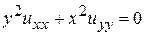 ,
, 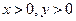 преобразовать к канонической форме.
преобразовать к канонической форме.
Решение. Вычислим дискриминант 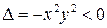 . Составим характеристические уравнения:
. Составим характеристические уравнения:
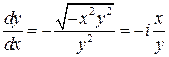 ,
, 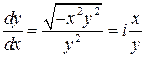 .
.
Решим их методом разделения переменных:
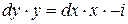 ,
, 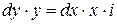
Интегрируя, получим 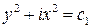 ,
, 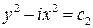 . Следовательно, новыми переменными будут
. Следовательно, новыми переменными будут
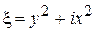 ,
, 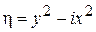 .
.
Введем вещественные переменные
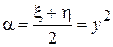 и
и 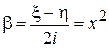 .
.
Вычисляя все коэффициенты нового уравнения по формулам (6) получим искомый канонический вид
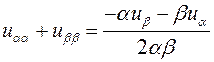 .
.
 2014-02-09
2014-02-09 1436
1436







