При модуляции одним током, когда S(t)=Cos(Ωt), тогда
a(t)=A0*(1+M*сos(Ωt))*сos(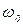 t)=A0*сos(
t)=A0*сos(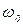 t)+
t)+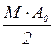 *сos(
*сos(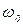 +Ω)*t+
+Ω)*t+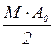 * сos(
* сos(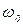 -Ω)*t (9.10)
-Ω)*t (9.10)
Здесь (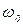 +Ω) - верхняя боковая частота
+Ω) - верхняя боковая частота
(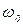 -Ω) - нижняя боковая частота.
-Ω) - нижняя боковая частота.
Спектр АМ- колебания представлен на рис. 9.2
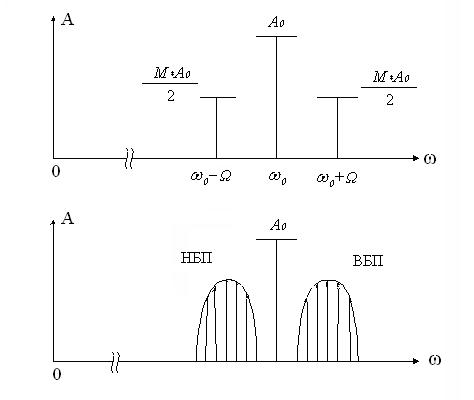
Ширина спектра АМ- колебания ∆w=2Ω.
Как в ВБП, так и в НБП- находится одна и та же информация о сигнале S(t).
Работа на одной боковой полосе ОБП (SSB- Single Side Band) позволяет уменьшить расход мощности от источников питания и полосу занимаемых АМ- сигналом частот.
9.4. Угловая модуляция. Фаза и мгновенная частота колебания.
Для простейшего гармонического колебания:
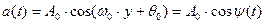 (9.11)
(9.11)
Набег фазы за конкретный промежуток времени от 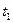 до
до 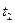 равен:
равен:
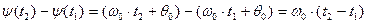 (9.12)
(9.12)
Из (9.12) видно, что при 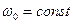 набег фазы за промежуток времени от
набег фазы за промежуток времени от 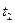 до
до 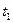 пропорционален длительности этого промежутка.
пропорционален длительности этого промежутка.
Из (9.12) также видно, что угловую частоту 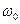 можно определить как отношение:
можно определить как отношение:
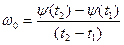 , (9.13)
, (9.13)
(если в течении времени от 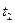 =
=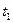 и
и 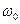 =const)
=const)
Из (9.13) видно, что угловая частота есть не что иное, как скорость изменения фазы колебания.
Для перехода к сложному колебанию, частота которого может изменяться во времени (9.12) и (9.13) необходимо заменить интегральным и дифференциальным соотношениями:
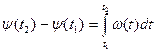 , (9.14)
, (9.14)
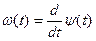 . (9.15)
. (9.15)
В этих выражениях:
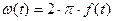 - есть мгновенная угловая частота колебания, а f(t) – мгновенная частота.
- есть мгновенная угловая частота колебания, а f(t) – мгновенная частота.
Согласно (9.14) и (9.15) полную фазу высокочастотного колебания в текущий момент времени t, можно определить как:
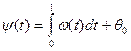 , (9.16)
, (9.16)
где 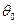 - начальная фаза в момент времени t=0;
- начальная фаза в момент времени t=0;
а 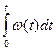 - определяет набег фазы за время от 0 до t.
- определяет набег фазы за время от 0 до t.
При таком подходе фазу 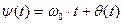 в (9.2) следует заменить на
в (9.2) следует заменить на 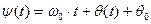 .
.
Таким образом, общее выражение для высокочастотного колебания, амплитуда которого постоянна [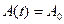 ], а фрагмент
], а фрагмент 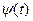 модулирован, то можно представить в форме:
модулирован, то можно представить в форме:
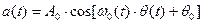 , (9.17)
, (9.17)
Соотношения (9.15) и (9.16), устанавливающие связь между изменениями частоты и фазы, указывают на общность двух разновидностей угловой модуляции: частотной модуляции и фазовой модуляции.
Роль соотношения (9.15) – (9.17) поясним на примере простейшей гармонической ЧМ, когда мгновенная частота колебания определяется выражением:
 , (9.18)
, (9.18)
где 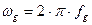 - представляет собой амплитуду частотного отклонения и называется девиацией частоты или просто девиацией.
- представляет собой амплитуду частотного отклонения и называется девиацией частоты или просто девиацией.
В (9.18) 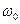 и
и 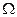 , как и при АМ, обозначены «несущая» и «модулирующая» частоты.
, как и при АМ, обозначены «несущая» и «модулирующая» частоты.
Если 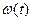 изменяется по закону (9.18), а амплитуда
изменяется по закону (9.18), а амплитуда 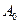 постоянна, то подставляя в (9.16)
постоянна, то подставляя в (9.16) 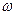 из (9.18) получаем:
из (9.18) получаем:
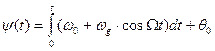 .
.
Выполнив интегрирование, получим для 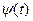
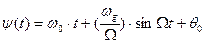 . (9.19)
. (9.19)
Таким образом:
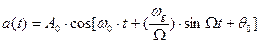 . (9.20)
. (9.20)
Видно, что фаза колебания 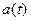 наряду с линейно-возрастающим слагаемым
наряду с линейно-возрастающим слагаемым 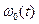 содержит еще периодическое слагаемое
содержит еще периодическое слагаемое 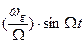 , т. е изменяется по закону модулирующей частоты
, т. е изменяется по закону модулирующей частоты 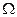 .
.
Это позволяет рассматривать 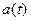 как колебание, модулированное по фазе.
как колебание, модулированное по фазе.
Закон этой модуляции является интегральным по отношению к закону изменения частоты. Именно модуляция частоты по закону 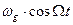 приводит к модуляции фазы:
приводит к модуляции фазы:
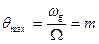 (9.21)
(9.21)
Параметр m – называют индексом угловой модуляции. Зачем, что индекс модуляции m не зависит от значения частоты несущей 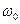 , а определяется исключительно значением девиации
, а определяется исключительно значением девиации 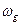 и значением модулирующей частоты
и значением модулирующей частоты 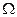 .
.
Рассмотрим теперь противоположный случай, когда стабильное по частоте и фазе колебания пропускаются через устройство, осуществляющее периодическую модуляцию фазы по закону:
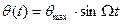 ,
,
так, что колебание на выходе устройства имеет вид:
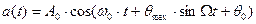 . (9.20’)
. (9.20’)
Учитывая (9.15) найдем частоту этого колебания
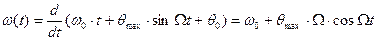 . (9.18’)
. (9.18’)
Учитывая (9.21) для 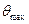 , приходим к выводу, что
, приходим к выводу, что 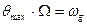 .
.
Таким образом, гармоническая модуляция фазы с индексом 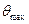 ,
,
эквивалентная частотной модуляции с девиацией:
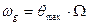
Из приведенного примера видно, что при гармонической угловой модуляции по характеру колебания нельзя заключить с какой модуляцией мы имеем дело с частотной или фазной. В обоих случаях угол 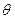 изменяется во времени по закону:
изменяется во времени по закону:
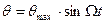 - при фазовой модуляции и
- при фазовой модуляции и
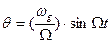 - при частотной модуляции, когда
- при частотной модуляции, когда 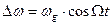
 2014-02-09
2014-02-09 1944
1944








