Алгоритм Крускала

Алгоритмы Крускала и Пpимa

Оба этих алгоритма следуют ранее описанной схеме, но по-разному выбира-
ют безопасное ребро. В алгоритме Крускала множество рёбер А представляет
собой лес, состоящий из нескольких связных компонент (деревьев). Добавляется
ребро минимального веса среди всех рёбер, концы которых лежат в разных
компонентах.

В алгоритме Прима множество А представляет собой одно дерево. Бе-
зопасное ребро, добавляемое к А, выбирается как ребро наименьшего веса,
соединяющее это уже построенное дерево с некоторой новой вершиной.

В любой момент работы алгоритма Крускала множество А выбранных рёбер
(часть будущего остова) не содержит циклов. Оно соединяет вершины графа в
несколько связных компонент, каждая из которых является деревом. Среди всех
рёбер, соединяющих вершины из разных компонент, берётся ребро наименьшего
веса. Надо проверить, что оно является безопасным.

Пусть (и, v) такое ребро, соединяющее вершины из компонент С ₁ и С ₂.
Это ребро является лёгким ребром для разреза (С ₁, V \ С ₁), и можно восполь-
зоваться теоремой 5.8 (или следствием 5.9).

Реализация алгоритма Крускала напоминает алгоритм вычисления связных
компонент и использует структуры данных для непересекаю-
щихся множеств. Элементами множеств являются вершины графа; каждое множество содержит вершины одной связной компоненты. Напомним, что FIND-SET(u) возвращает представителя множества, содержащего элемент и. Две вершины и и v принадлежат одному множеству (компоненте), если FIND-SET(u) = FIND-SET(v). Объединение деревьев выполняется процедурой UNION. (Строго говоря, процедурам FIND-SET и UNION должны передаваться указатели на и и v; для простоты мы опускаем соответствующие уточнения.)

Листинг 5.9 – Алгоритм Крускала

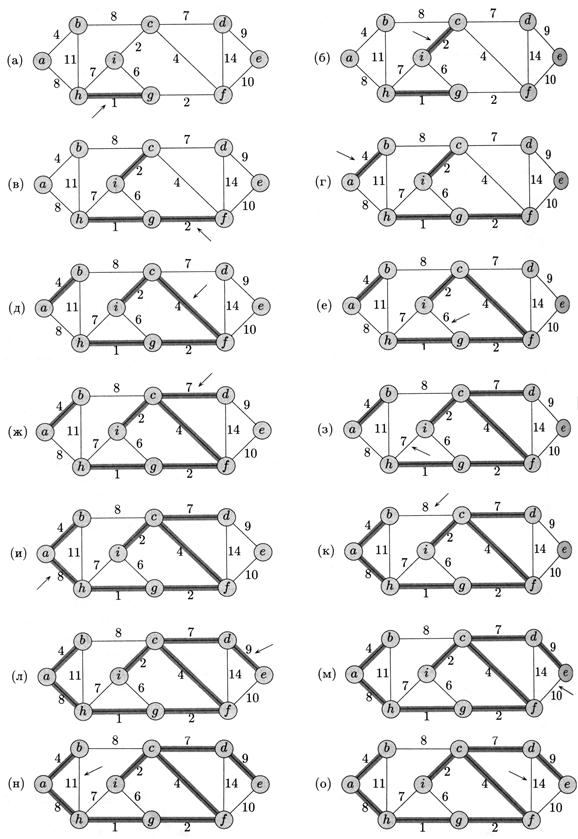
Рисунок 5.9 – Работа алгоритма Крускала

На рис. 5.9 показана работа алгоритма. Сначала (строки 1 – 3) мно-
жество А пусто, и есть | V | деревьев, каждое из которых содержит по одной
вершине. В строке 4 рёбра из E упорядочиваются по неубыванию веса. В цикле
(строки 5 – 8) мы проверяем, лежат ли концы ребра в одном дереве. Если да,
то ребро нельзя добавить к лесу (не создавая цикла), и оно отбрасывается.
Если нет, то ребро добавляется к А (строка 7), и два соединённых им дерева
объединяются в одно (строка 8).

Подсчитаем время работы алгоритма Крускала. Будем считать, что
для хранения непересекающихся множеств используется метод с объединением по рангу и сжатием путей самый быстрый из извест-
ных. Инициализация занимает время O (V), упорядочение рёбер в строке 4 – O (E × log Е). Далее производится O (E)операций, в совокупности занимающих
время O (E × 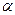(E, V)), где 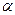функция, обратная к функции Аккермана. Поскольку 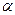(E, V) = O (log E), общее время работы алгоритма Крускала
составляет O (E × log E) (основное время уходит на сортировку).

На рисунке 5.9 рёбра растущего леса (А) выделены серым цветом. Рёбра рассматриваются в порядке неубывания весов (текущее
ребро показано стрелкой). Если ребро соединяет два различных дерева, оно добавляется к
лесу, а деревья сливаются.