Рынок ценных бумаг

Begin

Begin

Begin

Else

Then

Begin

End.

Begin

Begin

m:= (x1 + x2)/2.0;

If Abs(F(x2) – F(x1)) < eps Then Exit;

If F(m)*F(x1) < 0

Then x2:=m Else x1:=m;

Bisect (x1, x2);

End;

Вызов: ….. x1:= 0; x2:=5; Bisect(x1, x2); Вывод m; …….

Задача о разрезании прямоугольника. Из листа клетчатой бумаги разме-ром n∙m клеток вырезали образующие некоторые фигуры клетки. Линии разреза совпадают с границами клеток. Определить количество вырезанных фигур.

Матрицей А размерности n∙m моделиру­ется лист клетчатой бумаги, при этом

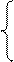1, если клетка вырезана;

A [ i,j ] =

0, если не вырезана;

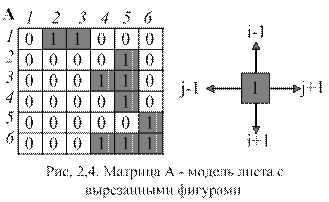Задание исходных данных — формирова­ние матрицы А — осуществляется с помо­щью генератора случайных чисел. Суть решения заключается в просмотре матрицы А до первой единицы. Как только встречаем единицу, то это означает, что мы вышли на очередную вырезанную фигуру. Поэтому следует изменить значе­ние счетчика числа вырезанных фигур cq и "погасить" все соседние единицы.

Рассмотрим на примере механизм «гашения» соседних единиц. На рис.2.4 показано, что вырезано три фигуры. Встретив первую "1" в клетке [ 1,2 ], мы должны просмотреть всех ее соседей во всех направлениях так, как это показано на рисунке. При анализе значений соседних клеток, во-первых, необходимо проверить, не вышли ли значения i и j за допусти­мые пределы, для i от 1 до n, для j от 1 до m, если "да", то проверку соседей в этом направлении следует прекратить и, во-вторых, если в соседней клетке записан 0, то проверку в этом направлении также следует прекратить. Итак, встретив 1 в клетке [ 1,2 ], мы просматри­ваем клетки в направлении (i-1) - выход за пре­делы листа, в направлении (i+1) - клетка не отно­сится к вырезанной фигуре (А [ 2,2 ] =0), в направ­лении (j-1) - клетка не относится к вырезанной фигуре (А [ 1,1 ] =0), в направлении (j+1) - клетка относится к вырезанной фигуре (A [ 1,3 ] =1). В этом случае мы должны присвоить А [ 1,3 ] значение 0 и рассмотреть клетку А [ 1,3 ] как начальную для га­шения единиц, соседних уже этой клетке. Рекурсивная процедура для реализации этого алгоритма приведена ниже.

Листинг 2.2. {Задача о разрезании прямоугольника.}

Procedure Clr (i, j:Integer); {гашение соседней клетки}

If (i In [1..n]) And (j In [1..m]) And (A[i, j] = 1) Then Begin

A[i, j]:= 0;

Clr (i - 1, j);

Clr (i+1, j);

Clr (i, j – 1);

Clr (i, j + 1);

End;

End;

Begin { Головная программа }

Вызов процедуры формирования матрицы А;

cq:= 0; {начальное значение счетчика фигур}

For i:= l To n Do

For j:= l To m Do

If A[i, j] > 0

Then Begin Inc(cq); Clr(i, j); End;

Wrteln ('Kоличество фигур = ', cq);

Раскраска области изображения. Дано изображение состоящее из одной или нескольких связных однотонных областей O_i и требуется разметить (раскрасить) каждую область некоторым заданным цветом с. Для простоты будем считать, что вначале все области имеют цвет с0. Растровое изображение задано на экране.Приведенный ниже алгоритм просматривает соседние с текущей точкой растра и размечает их цветом с. Переход к соседним точкам растра происходит рекурсивно. Процесс раскраски начинается из некоторой начальной точки (xn,yn)и заполняет все пространство связной области O_i. Каждая точка растра окружена четырьмя соседними точками, координаты которых отличаются от центральной в соответствии с таблицей смещений z (см. пример ниже). Первая строка таблицы z соответствует смещениям по x, а вторая – смещениям по y.

Листинг 2.3. {Раскраска области изображения }

Const {таблица смещений по x и y до соседних точек}

z:Array[1..2, 0..3] Of Integer =

{ ∆x } ((-1, 0, 1, 0,),

{ ∆y } (0, -1, 0, 1));

Procedure FillRec (x, y:Integer);

Var i:Integer;

PutPixel (x, y, c); {раскраска точки (x,y) }

For i:=0 To 3 Do {цикл просмотра 4-х соседних точек}

If GetPixel(x + z[1,i], y + z[2,i]) = c0 {если точка не раскрашена

Then FillRec(x + z[1,i], y + z[2,i]); переходим к ней}

End;

Замечание. Рекурсивный алгоритм раскраски можно представить в двух вариантах: "посмотрел-шагнул" и "шагнул-посмотрел". Другими словами, в первом случае мы сначала выбираем подходящее место для шага вперед и только потом делаем этот шаг (что очень хорошо сообразуется с правилами передвижения, скажем, по болоту). Во втором же случае мы сначала делаем шаг вперед и только потом проверяем, что же именно оказалось у нас под ногами. Все-таки "ходим" мы не по болоту и в любой момент можем "спастись" из неправильно выбранного пикселя.

Шарик в лабиринте. Шарик ставится на верхнюю строку лабиринта и может кататься вправо и влево, а также при наличии пустоты под ним, падать под действием тяжести вниз (рис.2.5). Написать процедуру, моделирующую движение шарика в лабиринте.

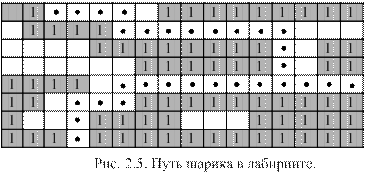Рекурсивная процедура Go на входе имеет текущие координаты (x,y)шарика. По этим координатам отмечаем положение шарика символом '●'. Далее проверяем, достиг ли шарик последней строки матрицы-лабиринта, если да – то лабиринт пройден и признак прохождения лабиринта p=true. Иначе исследуется окружение шарика: если внизу пусто, то перемещаем шарик вниз и возвращаемся из процедуры; если шарик может катиться по горизонтали, то вначале делается попытка переместить его вправо, а затем влево. Каждое перемещение шарика реализуется рекурсивным вызовом процедуры Go.

Листинг 2.4. {Шарик в лабиринте}

Const n=8; m=16;

Var a:Array [1..n] Of String[m]; {лабиринт}

p:Boolean; {признак достижения конца лабиринта (вначале p=False) }

Procedure Go (y, x:Byte); {процедура поиска пути в лабиринте}

Begin {x,y – текущие координаты шарика}

a[y,x]:='●';

If y = n Then Begin p:=True; Exit; End;

If a[ y+1, x ] = ' ' Then Begin Go (y + 1, x); Exit; End;

If (x < m) And (a[ y, x + 1] = ' ') Then Go (y, x + 1);

If (x > 1) And (a[ y, x – 1] = ' ') Then Go (y, x – 1);

End;

Задача о Ханойских башнях. 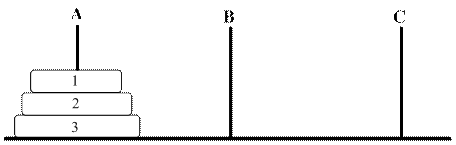Даны три столбика – А, В, С. На столбике А один на другом находятся четыре диска разного диаметра, пронумерованные сверху вниз. Причем они располага­ются так, что каждый меньший диск находится на большем. Требуется перемес­тить эти четыре диска на столбик С, сохранив их взаиморасположение. Столбик В раз­решается использо­вать как вспомогатель­ный. При решении за один шаг допускается переме­щать только один из верхних дисков ка­кого-либо столбика. Кроме того, больший диск никогда не разре­шается класть на диск меньшего диаметра.

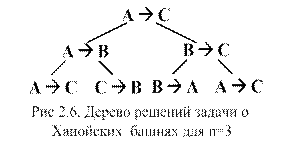Для определения подхода к решению поставленной задачи, рассмотрим слу­чай с тремя дисками. Рассуждения удобно иллюстрировать с помощью так называе­мого дерева решений (рис.2.6). Дейст­вительно, задача решается, если раз­бить ее на две подзадачи: переложить диски из А в B, а затем переложить их из B в C. Каждую из этих подзадач можно снова раз­бить на две подзадачи, как это показано на рисунке. Решение формулируется как рекурсивный обход дерева по правилу:

1. Обойти левое поддерево.

2. Попасть в корень.

3. Обойти правое поддерево.

Отсюда получается следующий порядок перестановки дисков:

AàС AàВ СàВ AàС ВàA ВàС AàС

Далее рассмотрим более общий случай с n дисками. Если мы сможем сформулировать решение для n дисков в терминах решения для n-1 диска, то поставленная проблема была бы решена, поскольку задачу для n-1 диска можно будет, в свою очередь, решить в терминах n-2 дисков и так далее до тривиального случая одного диска. Для случая одного диска (n=1) решение получается элементарным. Зада­чу перемещения n наименьших дисков со стержня А на стержень С можно представить себе состоящей из двух подзадач размера n - 1. Сначала нужно переместить n - 1 наи­меньших дисков со стержня А на стержень B, оставив на стержне А n -й наибольший диск. Затем этот диск нужно переместить с А на C. Потом следует переместить n - 1 дисков со стержня B на стержень C. Это перемещение n - 1 дисков выполняется путем рекурсивного применения указанного метода. Поскольку диски, участвующие в пере­мещениях, по размеру меньше тех, которые в перемещении не участвуют, не нужно задумываться над тем, что находится под перемещаемыми дисками на стержнях А, В или С. Хотя фактическое перемещение отдельных дисков не столь очевидно, а модели­рование вручную выполнить непросто из-за образования стеков рекурсивных вызо­вов, с концептуальной точки зрения этот алгоритм все же довольно прост для пони­мания и доказательства его правильности (а если говорить о быстроте разработки, то ему вообще нет равных). Именно легкость разработки алгоритмов по методу деком­позиции обусловила огромную популярность этого метода; к тому же, во многих слу­чаях эти алгоритмы оказываются более эффективными, чем алгоритмы, разработан­ные традиционными методами.

Таким образом, если сформулировать решение для n дисков в терминах n-1 диска, то мы фактически получим алгоритм рекурсивной процедуры, с помощью которой можно легко достичь цели поставленной задачи. Рассмотрим словесное описание такого алгоритма.

If n=l

Переместить этот единственный диск со столбика А на столбик С и

остановиться.

1. Переместить верхние n-1 диск со столбика А на

столбик В, используя столбик С как вспомогательный.

2. Переместить оставшийся нижний диск со столбика А

на столбик С.

3. Переместить n-1 диск со столбика В на столбик С,

используя столбик А как вспомогательный.

Приведем решение поставленной задачи с помощью рекурсивной процедуры.

{ Пусть n - число дисков на столбике S }

{ S - исходный столбик }

{ D - столбик, на который нужно переставить диски }
{ T - вспомогательный столбик }

Листинг 2.5. { Задача о Ханойских башнях }

Procedure Move (n: Byte; S, D, T: Char);
Begin

If n = 1

Then Writeln (' диск 1',S,'→', D)

Else Begin

Move (n-1, S, T, D); { 1 }

Writeln (' диск ',n:1,S,'→',D)

Move (n-1, T, D, S); { 2 }

End;

End;

{1} - переставляем n-1 верхних дисков с исходного столбика на

вспомогательный, используя целевой диск как промежуточный.

{2}- переставляем все п-1 дисков, расположенные на вспомогательном

столбике, на целевой, используя исходный диск как промежуточный.

Вызов: Begin ….. Move (n, 'А', 'С, 'В'); ….. End.

Результат работы программы для 4 исходных дисков на столбике А будет таким:

1 2 3 4 5 6 7 8

диск 1 А → В диск 2 А → С диск 1 В → С диск 3 А → В диск 1 С → А диск 2 С → В диск 1 А → В диск 4 А → С

9 10 11 12 13 14 15

диск 1 В → С диск 2 В → А диск 1 С → А диск 3 В → С диск 1 А → В диск 2 А → С диск 1 В → С

Быстрая сортировка. Сортировка методом простого обмена (методом "пузырька") является в среднем самой неэффек­тивной. Это обусловлено самой идеей метода, ко­торая требует в процессе сортировки сравнивать и

i→ ←j
								действие
								обмен
								i:= i+1
								i:=i+1
								i:=i+1
								обмен
								j:=j-1
								обмен
								i:=i+1
								обмен
								j:=j-1
(27			4)		(48		79)	результат
Рис. 2.7. Быстрая сортировка.

обменивать между собой только соседние элемен­ты. Можно существенно улучшить метод сорти­ровки, основанный на обмене. Это улучшение приводит к самому лучшему на сегодняшний день методу сортировки массивов, который можно на­звать обменной сортировкой с разделением. Он основан на сравнениях и обменах элементов, стоящих на возможно больших расстояниях друг от друга. Предложил этот метод Ч. Э. Р. Хоар в 1962 году. Поскольку производительность этого метода просто впечатляюща, автор назвал его QUICKSORT ("быстрой сортировкой").

В этом алгоритме[8] используется результат каждого сравнения, чтобы опре­делить, какие ключи сравниватьследующими. Итак, рассмотрим следующую схему сравнений/обменов. Имеются два указателя i и j, причем вначале i=1, a j = n. Сравним a [ i ] и a [ j ]и если обмен не требуется, то уменьшим j на единицу и повторим этот процесс. После первого обмена увели­чим i на единицу и будем продолжать сравнения, увеличивая i, пока не произойдет еще один обмен. Тогда опять уменьшим j и т. д.; будем "сжигать свечку с обоих концов", пока не станет i = j. Посмотрим, например, что произойдет с массивом из восьми чисел (рис. 2.7). Заметим, что в каждом сравнении этого примера участвует ключ х = 38; вообще в каждом сравнении будет присутствовать исходный ключ 38, потому что он будет продолжать обмениваться местами с другими ключами каждый раз, когда мы переключаем направление. К моменту, когда i = j, исходный ключ 38, займет свою окончательную позицию, потому что, как нетрудно видеть, слева от нее не будет больших ключей, а справа — меньших.

Исходный массив окажется разделен таким образом, что первоначальная задача сведется к двум более про­стым: сортировке массива a [ 1 ]..a [ i-1 ]и (независимо) сортировке массива a [ i+1 ]..a [ n ]. К каждому из этих подмассивов можно при­менить тот же самый метод, что явно указывает на возможность рекурсии. Исходный ключ 38 еще называют барьером; от значения барьера зависит насколько близки по длине образуются два полученных подмассива.

Алгоритм "быстрой" сортировки можно опре­делить как рекурсивную процедуру, параметрами которой являются нижняя и верхняя границы из­менения индексов сортируемой части исходного массива.

Алгоритм QUICKSORT

1. Возьмем в сортируемом массиве срединный элемент: m:=a[(1+n)div 2];

2. Будем производить следующие действия:

1. начав с левого конца массива, будем перебирать его компоненты до тех пор, пока не встретим элемент a[i], больший m;

2. начав с правого конца массива, будем перебирать его компоненты до тех пор, пока не встретим элемент a[j], меньший m;

3. поменяем местами элементы a[i] и a[j];

до тех пор, пока не произойдет «схлапывание». В результате массив будет разделен на две части. В левой части окажутся все компоненты, меньшие m, а в правой - большие m.

3. Теперь применим эти же действия к левой и к правой части массива - рекурсивно.

Листинг 2.6. { Рекурсивный алгоритм QUICKSORT }

Procedure QSortR (L, R:Integer); { Recursive sorting Hoar,1962}

Var i, j, m:Integer; { L, R – левая и правая границы сортируемой части массива }

i:= L; j:= R;

m:= a[ (R + L) Div 2 ]; {m - индекс середины сортируемой части массива }

Repeat {цикл встречного продвижения индексов i и j}

While a[ i ] < m Do Inc (i); {пока обмен не требуется, i → вперед}

While a[ j ] > m Do Dec (j); {пока обмен не требуется, j → назад}

If i <= j {если требуется обмен,

Then Begin Обмен a[i] ↔ a[j]; он производится и индексы

Inc(i); Dec(j); i и j перемещаются навстречу}

End;

Until i > j; {конец цикла, если произошло «схлапывание» индексов i и j}

If L < j Then QSortR (L, j); {QSortR от L до места «схлапывания» }

If i < R Then QSortR (i, R); {QSortR от места «схлапывания» доR}

End;

Вызов: Begin Ввод массива а; QSortR (1, n);Вывод массива а; End.

Замечание. В гл.10 будет показано, что производительность алгоритма в среднем характеризуется как O (n∙logn) и, следовательно, относится к улучшенным методам сортировки массивов. Кроме того, даже среди улучшенных методов упорядочения QUICKSORT дает наилучшие результаты по времени (для относительно больших входных последовательностей - начиная с n = 100). Итеративный вариант алгоритма QUICKSORT еще более эффективен. Существует, однако, "плохой" случай (и немногочисленные смежные с ним), когда эффективность QUICKSORT резко ухудшается до n². Это происходит, если на каждом шаге срединным оказывается такой элемент, что от массива отделяется всего один элемент (массив длины n распадается на два массива длины n -1 и 1). Поэтому при описании эффективности мы использовали слова "в среднем".

Рекурсивная сортировка слиянием. Существует еще один метод сортировки эле­ментов массива, эффективность которого сравни­тельно велика — метод слияния. Этот метод состоит в разбиении данного масси­ва на несколько частей, которые сортируются по отдельности, и в последующем составлении из не­скольких уже упорядоченных массивов искомого упорядоченного массива.

Пусть массив a [ 1..n ]разбивается на части дли­ной m, тогда первая часть — a [ 1 ], a [ 2 ],..., а [ m ],вто­рая — а [ m+1 ], a [ m+2 ],..., а [ 2m ]. Если n не делится на m, то в последней части будет менее m элементов. После того как массивы-части упорядочены, можно объединить их в упорядоченные массивы - части, состоящие не более,

								m=1
								m=2
								m=4
								m=8

чем из 2m элементов, которые далее объединить в упорядоченные мас­сивы длиной не более 4m и так далее, пока не по­лучится один отсортированный искомый массив. Вложенный характер сортировок и слияний частей массива является основой для рекурсивной реализации алгоритма. Таким образом, чтобы получить отсортирован­ный массив этим методом, нужно многократно "сливать" два упорядоченных отрезка массива в один упорядоченный отрезок. При этом другие части массива не затрагиваются. Пример сортировки слиянием приведен ниже.

Листинг 2.7. { Рекурсивная сортировка слиянием }

Procedure AddSort (L, R: Integer); {сортировка слиянием}

{ L, R, m – границы объединяемых подмассивов: (L..m), (m+1..R) }

Var m:Integer;

If L < R Then Begin

m:= (L+R) Div 2; {определяем границы подмассивов}

AddSort (l, m); {сортируем первый подмассив a[1..m]}

AddSort (m+1, R); {сортируем второй подмассив a[m+1..R}

Merge (L, m, R); {объединяем слиянием два подмассива}

End;

End;

После сортировки двух массивов - частей необходимо их слияние процедурой Merge. Основная идея алгоритма Merge состоит в сравнении очередных элементов каждой части, выяснении, какой из них меньше, переносе его в динамический массив с, ко­торый является вспомогательным, и продвижении по тому массиву-части, из которого взят элемент. Когда одна из частей будет пройдена до конца, ос­танется только перенести в с оставшиеся элементы второй части, сохраняя их порядок. При завершении процедуры массив с копируется в а ипамять, отведенная для нее, освобождается. Динамический характер массива с обусловлен ее необходимой переменной длиной. Можно отметить, метод сортировки слиянием имеет производительность в среднем O (n log n).

Листинг 2.7.1. {Объединяет слиянием два отсортированных подмассива}

Procedure Merge (L, m, R:Integer);

Var i, j, k, s, t:Integer;

i:= L; { i – индекс для первого подмассива}

j:= m+1; { j – индекс для второго подмассива}

k:=1; { k – индекс для массива с }

While (i <= m) And (j <= R) Do { цикл слияния в массив с }

If a[i] < a[j] Then Begin c[k]:= a[i]; Inc(i); Inc(k); End

Else Begin c[k]:= a[j]; Inc(j); Inc(k); End;

If i>m Then Begin s:=j; t:=R; End

Else Begin s:=i; t:=m; End;

For i:=s To t Do

Begin c[k]:= a[i]; Inc(k); End; {перенос остатка}

Move (c, a[L], 2*(R - L+1)); {копирование c→a }

End;

Вызов: ….. Ввод массива а; AddSort (1, n);Вывод массива а; ……

Резюме. Итак, что хочется сказать. Во-первых, рекурсия сама по себе не является алгоритмом, она является методом построения алгоритмов. Ее очень удобно применять (но не обязательно эффективно) в тех случаях, когда можно выделить самоподобие задачи, т.е. свести вычисление задачи некоторой размерности N к вычислению аналогичных задач меньшей размерности.

Во-вторых, если получается сделать алгоритм без применения рекурсии, то, скорее всего, им и надо воспользоваться. Рекурсивные вызовы подпрограмм имеют свойство решать одну и ту же задачу бесчисленное количество раз (во время повторов), что значительно сказывается на времени. Самым ярким примером является традиционное вычисление чисел Фибоначчи рекурсивным и тем не менее, бывают случаи, когда переход к рекурсии от хорошего итеративного алгоритма будет давать преимущества, несмотря на то, что реализованы одинаково. Это алгоритмы, в которых используется стек.

Вообще говоря, стек и рекурсия взаимозаменяемы. То есть, все что можно сделать при помощи рекурсии, можно заменить на "условно бесконечный" цикл с использованием стека и наоборот. Это очень часто используется тогда, когда размер системного стека (того, в который помещается адрес возврата и где выделяется память под локальные переменные) сильно ограничен какими-то аппаратными особенностями; в таких случаях реализуют стек самостоятельно и имитируют вызов подпрограммы путем работы с этим "доморощенным" стеком.

Тем не менее, аппаратный стек несколько быстрее, чем стек, реализованный самостоятельно. Поэтому в некоторых случаях, когда используется стек (например, для вычисления значения выражения, для перевода выражения из инфиксной в постфиксную форму и т.д.) небольших размеров, имеет смысл использовать рекурсию для того, что бы воспользоваться аппаратными возможностями по его организации.

Особенно стоит отметить, что при использовании рекурсивных подпрограмм важен вопрос о выделении памяти под локальные переменные. Все дело в том, что когда разворачивается рекурсивный вызов, на каждый конкретный вход в подпрограмму будет израсходована память под все локальные переменные. Это значит, что их использование должно быть сведено к минимуму, иначе память может закончиться раньше, чем вычислится значение выражения.

Рекурсивные функции очень опасны. Несмотря на то, что существует множество задач, на решение которых прямо напрашивается рекурсия, не стоит сразу же бросаться реализовывать рекурсивные вызовы. Вполне вероятно, что все это обернется либо большими и неоправданными расходами оперативной памяти, либо будет очень медленно работать. Т.е., как обычно: прежде чем что-то делать, надо подумать, обвешать все острые места красными флажками, а после этого делать итеративным способами.