Решение линейных алгебраических систем методом Монте-Карло

Существует множество методов решения линейных алгебраических систем методом статистических испытаний[2]. Рассмотрим метод применимый к решению системы линейных алгебраических уравнений общего вида

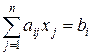, (9)

где i = 1,…, n.

Решение системы (9) равносильно минимизации квадратичной формы:

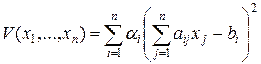, (10)

где a ₁, a ₂, …, a_n — некоторые положительные константы.

Учитывая (10), определим n -мерный эллипсоид

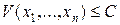. (11)

Пусть 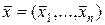— вектор решения системы уравнений (9), тогда очевидно, что вектор 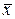является центром симметрии эллипсоида (11). Это означает, что каждая из гиперплоскостей 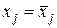, проходящая через центр эллипсоида, делит его объем пополам. По этой причине решение системы (9) сводится к нахождению таких значений 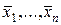, что объемы частей эллипсоида, лежащих в полупространствах 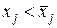и 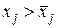совпадают и равняются половине объема эллипсоида (11).

Из данных соображений вытекает следующий способ решения. Возьмем n -мерный параллелепипед

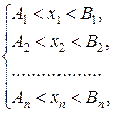
в который заведомо помещается n -мерный эллипсоид.

Рассмотрим статистическую серию из N векторов

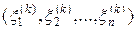, (12)

где k = 1,2,…, N и случайная компонента 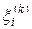равномерно распределена на отрезке [ A_i, B_i ], i = 1,…, n.

Отберем среди набора векторов (12) те, которые попадают в эллипсоид (11), т.е. удовлетворяют условию 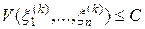. Пусть таких векторов оказалось M. Рассмотрим среднее арифметическое 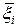векторов, попавших в эллипсоид, тогда можно записать следующее представление:

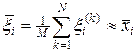, (13)

из которого следует способ нахождения вектора 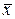решений исходной системы уравнений (9).

Можно оценить дисперсию случайной величины (13). Она равна

,

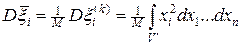где V ¢ — n -мерный объем, удовлетворяющий неравенству .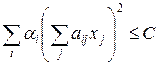

На листинге_№6 приведен код программы, которая решает систему уравнений (9) методом Монте-Карло согласно алгоритму (13).

Листинг_№6

%Задача решения линейной алгебраической системы

%уравнений ax=b методом Монте-Карло

function linear

%Определяем размерность системы уравнений (9)

n=100;

%Определяем вектор решений x0 системы уравнений (9)

for i=1:n

x0(i)=i;

end

%В качестве матрицы a выбираем случайную матрицу,

%а правую часть b находим из уравнения b=ax0

a=randn(n,n); b=a*x0';

%Определяем параллелепипед, в который помещается

%эллипсоид

for i=1:n

A(i)=x0(i)-10; B(i)=x0(i)+10;

end

%Оцениваем константу С, входящую в определение

%эллипсоида (11)

for i=1:n

xi(i)=A(i)+(B(i)-A(i))*rand;

end

for k=1:100

for i=1:n

xi(i)=A(i)+(B(i)-A(i))*rand;

end

W(k)=V(a,b,xi);

end

C=0.5*(min(W)+max(W));

%Организуем цикл расчетов с разными длинами

%статистических серий N

m=0;

for N=1000:5000:71000

M=0; x=zeros(1,n);

for k=1:N

for i=1:n

xi(i)=A(i)+(B(i)-A(i))*rand;

end

if V(a,b,xi)<=C

M=M+1;

x=x+xi;

end

end

x=x/M;

m=m+1;

%Определяем относительную ошибку численного

%решения x к точному решению x0

error(m)=norm(x-x0)/norm(x0);

lng(m)=N;

end

%Рисуем зависимость относительной ошибки от длины

%статистической серии N

loglog(lng,error);

%Определяем квадратичную форму (10)

%(alpha1=...=alphan=1)

function y=V(a,b,x)

y=0;

for i=1:length(x)

s=0;

for j=1:length(x)

s=s+a(i,j)*x(j);

end

y=y+(s-b(i))^2;

end

На рис.6 приведен итог работы кода программы листинга_№6. На фигуре изображена кривая, изображающая динамику относительной ошибки error = || x - x ₀||/|| x ₀||, где x — численное решение системы уравнений (9), а x ₀ — точное решение системы уравнений (9).

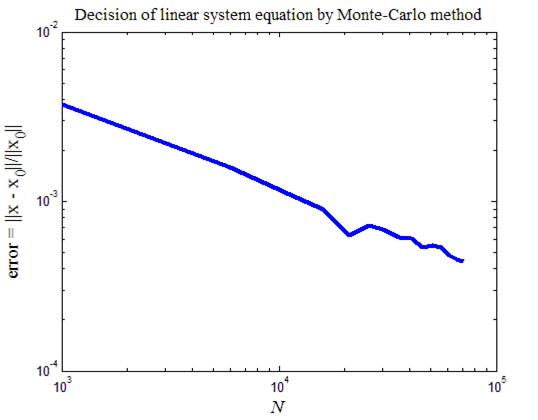
Рис.6. Решение линейной системы уравнений (9) методом
Монте-Карло