Вычисление интегралов

Значение случайной функции f (x) заключено между f (x) и f (x + dx), если случайная величина x заключена между x и x + dx. Вероятность такого события равна r (x) dx. В этом случае математическое ожидание и дисперсия случайной функции можно оценить согласно формулам:

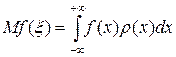, (14)

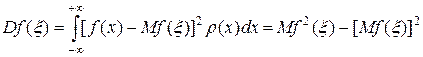. (15)

Первый способ вычисления интегралов с помощью метода Монте-Карло базируется на формуле (14), т.е. одномерный интеграл можно рассматривать как математическое ожидание случайной функции f (x), аргумент которой является случайной величиной с плотностью распределения r (x).

Математическое ожидание можно приближенно вычислить, исходя из центральной предельной теоремы теории вероятностей. Если h является случайной величиной, то среднее арифметическое N испытаний

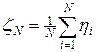
также является случайной величиной с тем же математическим ожиданием, т.е. 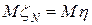, при это распределение случайной величины 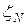стремится к нормальному распределению с дисперсией 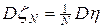при N ® ¥. Таким образом, при большом числе испытаний дисперсия 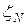будет малой величиной, а значение средней арифметической с вероятностью близкой к единице будет близко к математическому ожиданию. Учитывая эти соображения, можно положить

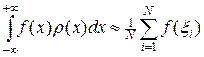, (16)

где x — случайная величина с плотностью распределения r (x).

Оценим дисперсию (15), заменяя в ней математические ожидания на соответствующие суммы типа (16), тогда

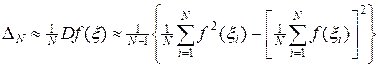. (17)

Делитель N - 1 вместо N в (17) связан с тем соображением, что для оценки выборочной дисперсии используется так называемая несмещенная оценка. Впрочем, это существенно лишь при малой длине выборки N.

При статистических испытаниях численные оценки тех или иных величин носят вероятностный характер, т.е. они в принципе могут как угодно сильно отличаться от точного значения. Однако, согласно свойствам нормального распределения, с вероятностью 99,7% ошибка не превосходит три стандартных отклонения, т.е. величины 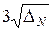. При увеличении числа статистических испытаний N ошибка ответа будет уменьшаться, примерно, как 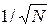. Отметим, что зависимость 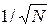относится не к самой ошибке, а к тем доверительным интервалам, в которые ошибка попадает с заданной вероятностью.

В качестве примера найдем методом статистических испытаний интеграл

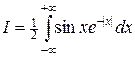, (18)

значение которого равно нулю. Применим к интегралу формулы (15), (16), тогда получим следующие расчетные формулы

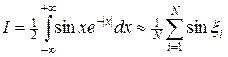, (19)

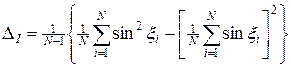, (20)

где x — случайная величина с плотностью 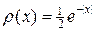, 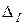— выборочная дисперсия. Случайную величину x для решения задачи (18) — (20) разыграем согласно формуле (7), где g — равномерно распределенная на отрезке [0,1] случайная величина, генерируемая с помощью генератора псевдослучайных чисел (5) с параметрами A = 5¹³ и g ₀ = 2^-36.

На листинге_№7 приведен код программы взятия интеграла (18) методом Монте-Карло по формулам (19), (20).

Листинг_№7

%Пример взятия интеграла (18) методом статистических

%испытаний согласно формулам (19), (20)

clear all

%Задаем число удвоений числа статистических испытаний

nmax=22;

%Задаем значения констант A и gamma0 для генерации

%согласно алгоритму (5) псевдослучайных чисел,

%распределенных равномерно на отрезке [0,1]

A=5^13; gamma0=2^(-36);

%Организуем цикл расчетов с различным числом

%статистических испытаний N

for n=1:nmax

N=2^n;

%Генерируем последовательность псевдослучайных

%чисел gamma, согласно алгоритму (5), а также

%случайные числа xi с плотностью 0.5*exp(-abs(x))

gamma=gamma0; I(n)=0; s=0;

for i=1:N

gamma=mod(A*gamma,1);

if gamma>=0.5

xi=log(1.0/(2-2*gamma));

else

xi=log(2*gamma);

end

sxi=sin(xi);

I(n)=I(n)+sxi; s=s+sxi^2;

end

%Вычисляем искомый интеграл I и соответствующую

%дисперсию delta согласно формулам (19), (20)

I(n)=I(n)/N; delta=(s/N-I(n)^2)/(N-1);

%Вычисляем доверительный интервал con_int с

%99,7% надежностью

con_int(n)=3*sqrt(delta);

%Определяем массив с числом испытаний в каждом

%статистическом эксперименте

lng(n)=N;

end

%Рисуем сходимость численного значения интеграла (18)

%в зависимости от числа испытаний N в отдельном

%статистическом эксперименте

subplot(1,2,1); loglog(lng,abs(I));

%Рисуем зависимость длины доверительного интервала с

%99,7% надежностью от числа испытаний N в отдельном

%статистическом эксперименте

subplot(1,2,2); loglog(lng,con_int);

На рис.7 приведен итог работы кода программы листинга_№7. На левом рисунке приведена зависимость абсолютного значения искомого интеграла от числа испытаний в статистическом эксперименте (все координаты выбраны логарифмическими). Видна сходимость в среднем численной оценки к искомому значению интеграла, равному нулю. На правом рисунке приведена зависимость границы доверительного интервала с надежностью 99,7% от числа испытаний в статистическом эксперименте. Согласно определению доверительного интервала, введенному в выборочном методе статистики, искомое значение интеграла I с вероятностью» 99,7% находится в интервале

.

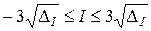Рис.7. Численное взятие интеграла (18) методом Монте-Карло

Второй метод взятия интеграла методом статистических испытаний применяется к интегралам вида 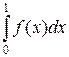, при этом считается, что 0 £ f (x) £ 1, x Î [0,1]. Произвольный интеграл можно привести к такому виду некоторой линейной заменой переменных.

Пусть имеется набор из N пар {(g ₁, g ₂),(g ₃, g ₄),…,(g _{2 N -1},g_{2 N})}, равномерно распределенных на единичном отрезке случайных чисел. Рассмотрим пары чисел 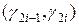как координаты точек 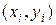единичного квадрата координатной плоскости x и y (левый график на рис.8).

Поскольку точки на плоскости распределены случайно и равномерно в единичном квадрате, постольку вероятность попадания точки под кривую y = f (x) равна площади, заключенной под кривой, т.е. искомому интегралу I = 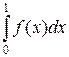. Условие попадания точки 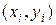под кривую определяется неравенством 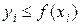. Доля точек из всего набора N точек, которая удовлетворяет данному неравенству, дает приближенное значение искомого интеграла.

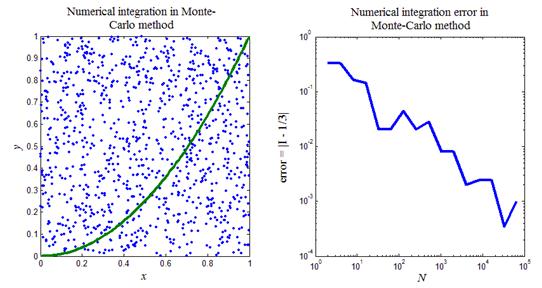
Рис.8. Взятие интеграла 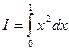методом статистических испытаний

На листинге_№8 приведен код программы численного взятия интеграла 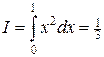методом статистических испытаний.

Листинг_№8

%Пример взятия интеграла от функции y=x^2 вторым

%способом в методе статистических испытаний

clear all

%Создаем массив точек на плоскости (x,y) со

%случайными, равномерно распределенными на

%единичном отрезке числами

N=1000;

for i=1:N

x(i)=rand; y(i)=rand;

end

%Определяем подынтегральную функции yi=xi^2

xi=0:0.01:1;

for i=1:length(xi)

yi(i)=xi(i)^2;

end

%Рисуем массив случайных точек и

%подынтегральную функцию

subplot(1,2,1);

plot(x,y,'.',xi,yi,'LineWidth',3);

%Определяем число удвоений числа точек на

%плоскости, координаты которых равномерно

%распределены на единичном отрезке

nmax=16;

%Организуем цикл расчетов искомого интеграла

%для различного количества случайных точек на

%плоскости

for n=1:nmax

N=2^n; I=0;

for i=1:N

x(i)=rand; y(i)=rand;

if y(i)<=x(i)^2

I=I+1;

end

end

%Вычисляем искомый интеграл

I=I/N;

%Оцениваем ошибку численного интегрирования

%методом статистических испытаний

error(n)=abs(I-1.0/3);

lng(n)=N;

end

%Рисуем зависимость ошибки численного

%интегрирования от количества точек N

subplot(1,2,2); loglog(lng,error);

На рис.8 приведен итог работы кода программы листинга_№8. На левом рисунке приведен график подынтегральной функции y = x ², а также N = 1000 случайных точек в единичном квадрате. Подсчитывалась доля точек, которые оказывались ниже кривой y = x ². На правом рисунке изображена зависимость ошибки численного интегрирования error = | I - 1/3| от параметра N — числа точек в статистической серии. Видно, что в среднем, по мере роста параметра N, ошибка численного интегрирования стремится к нулю.

Оптимизация дисперсии. Точность взятия интеграла методом Монте-Карло можно повысить, подбирая специальным образом случайную величину. Пусть g (x) = f (x) r (x), тогда исходный интеграл запишется в виде: 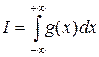, где функция r (x) нормирована таким образом, что ее можно считать плотностью распределения некоторой случайной величины. Задача состоит в том, чтобы, путем подбора плотности распределения r (x), добиться минимума дисперсии (15).

В дисперсии отдельного испытания (15) второе слагаемое 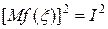, оно не зависит от плотности r (x), поэтому условие минимума сводится к условию:

.

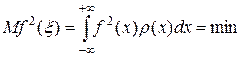Добавляя условие нормировки плотности r (x), получим следующую задачу оптимизации:

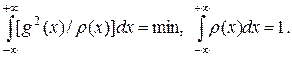
Находя вариационные производные и приравнивая их нулю, получим

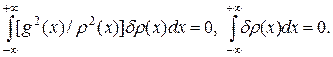
Для равенства вариационных производных нулю необходимо и достаточно, чтобы 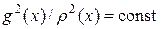, т.е. 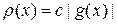. В этом случае дисперсия не просто минимальна, а равна нулю, когда g (x) знакопостоянна.

На практике взять 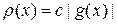не удается, т.к. для моделирования случайной величины с такой плотностью необходимо решить уравнение

,

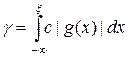которое равносильно по сложности исходной задаче взятия интеграла I. По этой причине плотность r (x) подбирают так, чтобы уравнение

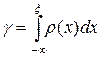
относительно x решалось просто, а сама плотность r (x) была как можно ближе к g (x).

Смысл увеличения точности состоит в том, что, если r (x) ~ | g (x)|, то f (x) почти постоянна и все испытания дают близкие результаты.

В качестве примера рассмотрим взятие интеграла

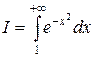» 0.13940279264033. (21)

Будем считать, что 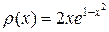, при этом 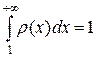. Случайную величину с такой плотностью разыгрываем согласно формуле

.

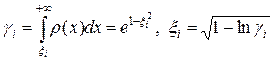Откуда следует, что

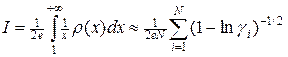, (22)

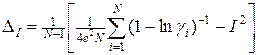. (23)

На листинге_№9 приведен код программы взятия интеграла (21) с помощью алгоритма статистических испытаний с уменьшенной дисперсией, т.е. с помощью вычислительных формул (22), (23).

Листинг_№9

%Взятие интеграла (21) методом Монте-Карло

%с уменьшенной дисперсией по формулам (22), (23)

clear all

%Определяем число удвоений количества чисел

%в статистической серии

nmax=20;

%Организуем цикл расчетов с различными

%длинами статистических серий

for n=1:nmax

N=2^n; I=0; s=0;

for i=1:N

g=1.0/sqrt(1-log(rand));

I=I+g;

s=s+g^2;

end

%Определяем искомый интеграл (21) согласно

%вычислительной формуле (23)

I=I/(2*exp(1.0)*N);

%Определяем дисперсию численной оценки

%искомого интеграла

delta=(s/(4*exp(2.0)*N)-I^2)/(N-1);

%Определяем ошибку численной оценки

%искомого интеграла

error(n)=abs(I-0.13940279264033);

%Определяем границу доверительного интервала

%с надежностью 99,7%

con_int(n)=3*sqrt(delta);

lng(n)=N;

end

%Рисуем зависимость ошибки численной оценки

%интеграла от количества испытаний N в

%статистической серии

subplot(1,2,1); loglog(lng,error);

%Рисуем зависимость границы 99,7% надежности от

%количества испытаний N в статистической серии

subplot(1,2,2); loglog(lng,con_int);

На рис.9 приведен итог работы кода программы листинга_№9. На левом рисунке приведена зависимость ошибки численного интегрирования от длины статистической серии. По сравнению с предыдущим примером точность заметно повысилась. На правом рисунке приведена зависимость границы доверительного интервала с 99,7% надежностью от длины статистической серии. Этот график заметно отличается от аналогичного графика, представленного на рис.7. При одной и той же длине статистической серии N границы доверительного интервала значительно уже в данном случае, чем в том примере, который приведен на рис.7 и где процедура оптимизации дисперсии не проводилась.

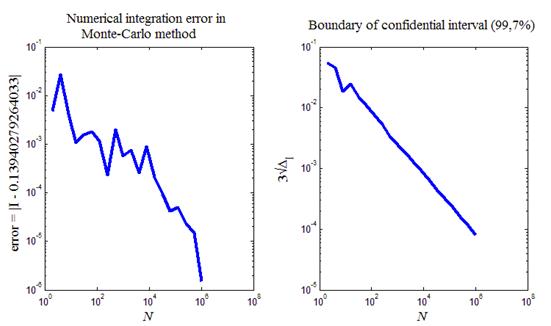
Рис.9. Взятие интеграла (20) методом статистических испытаний с
уменьшенной дисперсией

Многомерные интегралы. Второй способ легко обобщается на многомерные интегралы по единичному кубу G, если значения подынтегральной функции лежат в единичном интервале.

Рассмотрим для определенности трехмерное пространство с координатами x, y, z и интеграл вида

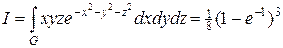. (24)

Интеграл (24) легко берется путем его факторизации и взятием трех одномерных интегралов.

Пусть определена совокупность N четверок (g ₁, g ₂, g ₃, g ₄), (g ₅, g ₆, g ₇, g ₈), …, (g _{4 N -3}, g _{4 N -2}, g _{4 N -1}, g _{4 N}), равномерно распределенных на единичном интервале случайных чисел. Каждая из четверток определяет случайную точку в единичном четырехмерном кубе 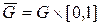. Доля случайных точек, удовлетворяющих неравенству 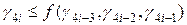, где 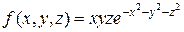определяет приближенное значение искомого интеграла.

На листинге_№10 приведен код программы взятия интеграла (24) вторым способом в методе статистических испытаний.

Листинг_№10

%Численное интегрирование вторым способом в

%методе статистических испытаний на примере

%взятия многомерного интеграла (24)

clear all

%Определяем число удвоений количества точек N

%в статистической серии

nmax=22;

for n=1:nmax

N=2^n; I=0;

%Вычисляем искомый многомерный интеграл

for i=1:N

x=rand; y=rand; z=rand; u=rand;

if u<=x*y*z*exp(-x^2-y^2-z^2)

I=I+1;

end

end

I=I/N;

%Оцениваем ошибку численного интегрирования

error(n)=abs(I-(1-exp(-1.0))^3/8);

lng(n)=N;

end

%Рисуем зависимость ошибки численного

%интегрирования от числа точек N в

%статистической серии

loglog(lng,error);

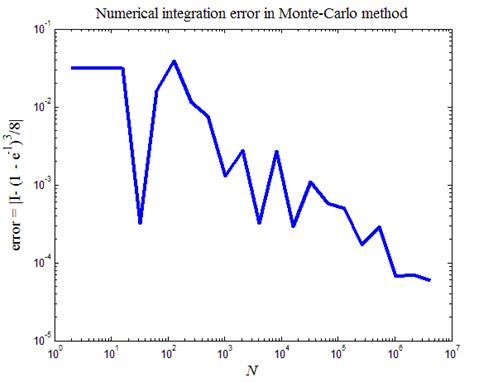
Рис.10. Зависимость ошибки численного интегрирования при взятии
интеграла (24) от числа точек N в статистической серии

На рис.10 приведен итог работы кода листинга_№10. Построена кривая, описывающая зависимость ошибки численного интегрирования методом статистических испытаний от длины N статистической серии. Из графика видно, что при N = 2²²» 4,2×10⁶ точность лучше 10^-4.

Рассмотренный выше второй способ вычисления кратных интегралов менее точен, чем первый способ. Рассмотрим более подробно процедуру использования первого способа при подсчете кратных интегралов методом статистических испытаний. Обозначим через r (x, y, z) ³ 0 многомерную плотность распределения некоторой случайной величины, тогда по аналогии с одномерным случаем, имеем

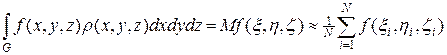. (25)

Взятие интеграла согласно способу (25) сводится к разыгрыванию многомерной случайной величины. Для разыгрывания первой переменной x построим одномерную плотность распределения по этой переменной при произвольных остальных

.

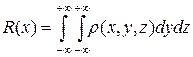Функция R (x) неотрицательна и нормирована на единицу, т.е. является плотностью некоторой случайной величины, поэтому можно записать следующую формулу разыгрывания:

,

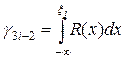где g _{3 i -2} — случайная величина, равномерно распределенная на единичном отрезке.

Найдем плотность распределения по второй координате y при фиксированной первой и произвольной третьей. Как нетрудно проверить, искомая плотность имеет вид:

.

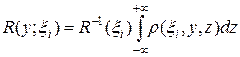В этом случае разыгрывание второй координаты сводится к решению уравнения

.

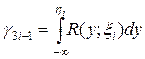Плотность распределения по третьей координате z при фиксированных первых двух имеет вид:

.

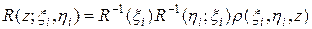Откуда следует последняя формула разыгрывания

.

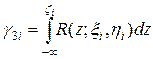В качестве примера вычисления интеграла вторым способом рассмотрим интеграл вида:

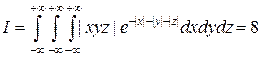. (26)

В качестве многомерной плотности распределения возьмем функцию 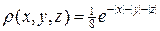. Функции r соответствуют одномерные плотности распределения вида:

,

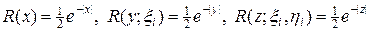где

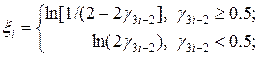
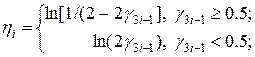(27)

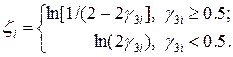
С учетом (27) расчетная формула для вычисления интеграла (26) запишется в виде:

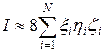. (28)

На листинге_№11 приведен код программы численного взятия интеграла (26) с помощью первого способа в методе статистических испытаний. С учетом вида случайных величин (27), расчетная формула для искомого интеграла приведена в (28).

Листинг_№11

%Программа расчета многомерного интеграла

%(26) с помощью первого способа в методе

%статистических испытаний по расчетной

%формуле (28)

clear all

%Определяем количество удвоений числа точек

%N в серии статистических испытаний

nmax=22;

for n=1:nmax

N=2^n; I=0;

%Определяем случайные величины xi, eta и dz,

%используемые в расчетной формуле (28)

for i=1:N

gmxi=rand; gmeta=rand; gmdz=rand;

if gmxi>=0.5

xi=log(1.0/(2-2*gmxi));

else

xi=log(2*gmxi);

end

if gmeta>=0.5

eta=log(1.0/(2-2*gmeta));

else

eta=log(2*gmeta);

end

if gmdz>=0.5

dz=log(1.0/(2-2*gmdz));

else

dz=log(2*gmdz);

end

I=I+abs(xi*eta*dz);

end

%Определяем искомый интеграл

I=(8.0/N)*I;

%Оцениваем ошибку численного расчета

%искомого интеграла

error(n)=abs(I-8);

lng(n)=N;

end

%Рисуем зависимость ошибки численного

%интегрирования от количества случайных

%точек N в статистической серии

loglog(lng,error);

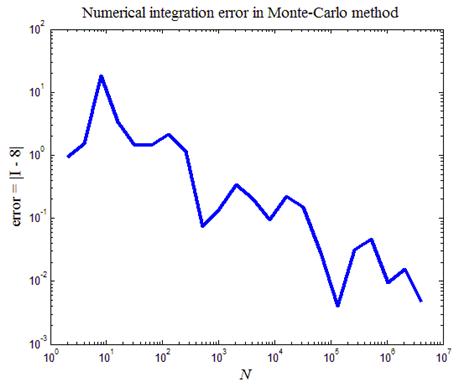
Рис.11. Зависимость ошибки численного интегрирования при взятии
интеграла (26) от числа точек N в статистической серии

На рис.11 приведен итог работы кода программы листинга_№11. Построена кривая, описывающая зависимость ошибки численного интегрирования методом статистических испытаний от длины N статистической серии. Видно, что в среднем точность растет по мере роста числа точек в статистической серии.

Обсудим вопрос о соотношении сеточных и статистических методов численного интегрирования. Пусть функция m переменных интегрируется с помощью некоторого сеточного метода p -го порядка точности. Будем считать, что сетка по каждой из переменных имеет n узлов. В этом случае полное число узлов есть N = n^m, а погрешность расчета e ~ n ^{- p}. Исключая n из последних двух соотношений, находим число узлов необходимое для достижения заданной точности 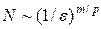. При использовании одного из методов статистических испытаний погрешность 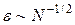, т.е. число случайных точек в статистической серии .

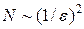Из сравнения двух формул 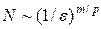и 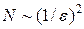следует, что при m < 2 p сеточные методы являются более предпочтительными, т.к. требуют меньшего числа узлов и, наоборот, при m > 2 p более предпочтительными являются статистические методы. Последнее неравенство указывает на то, что для численного взятия многомерных интегралов предпочтительными являются методы статистических испытаний.

Пусть, например, подынтегральная функция имеет непрерывные вторые производные, тогда можно рассчитывать на второй порядок точности, т.е. p = 2. В этом случае трехмерные интегралы, согласно вышеупомянутым неравенствам, выгодно интегрировать сеточными методами, а пятимерные — статистическими.