Метод Гаусса. Рассмотрим теперь систему m линейных уравнений с n неизвестными

Рассмотрим теперь систему m линейных уравнений с n неизвестными.

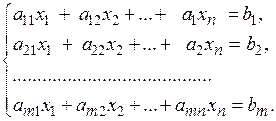(5.9)

Для решения системы (5.9) преобразуем ее в более простую. При этом можно применять лишь такие преобразования, которые переводят систему в равносильную. К ним относятся:

1) перемена местами двух уравнений в системе;

2) умножение уравнения на любое число, не равное нулю;

3) прибавление к одному уравнению другого, предварительно умноженного на произвольное число;

4) вычеркивание уравнений вида 0=0 (нулевых уравнений).

Преобразования вида 1, 2, 3, 4 называются элементарными.

Теорема 5.4. Элементарные преобразования системы линейных уравнений переводят систему в эквивалентную ей.

□ Для преобразований вида 1, 4 утверждение теоремы очевидно. Докажем, что преобразование вида 3 переводит систему (5.9) в эквивалентную.

В системе

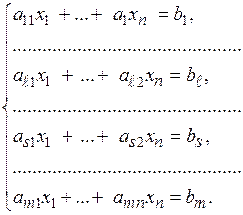(5.10)

прибавим к 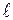-му уравнению 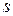-е уравнение, умноженное предварительно на некоторое число l. Получим систему вида

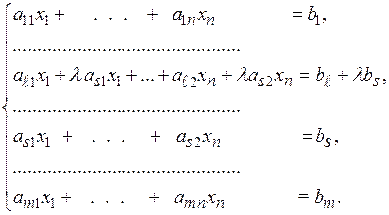(5.11)

Покажем, что системы (5.10) и (5.11) равносильны.

1. Пусть система (5.10) совместна и К = (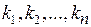) – решение
этой системы. К = (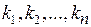) будет решением системы (5.11), если подстановка его в каждое уравнение системы обратит уравнение в верное равенство. Системы (5.10) и (5.11) отличаются только 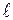-м уравнением, поэтому все остальные равенства выполняются автоматически. Подставляя К=(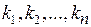) в 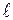-е уравнение системы (5.11), получим

.

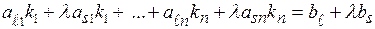Перегруппируем слагаемые:

.

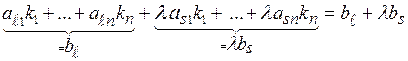Значит, каждое решение системы (5.10) является решением
системы (5.11).

2. Пусть теперь К = (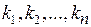) является решением системы (5.11). Прибавим к 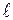-му уравнению системы (5.11) 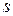-е уравнение, предварительно умноженное на (–l):

,

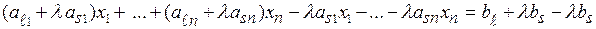или .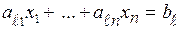

Мы пришли к системе (5.10), которая эквивалентна системе (5.11), так как было выполнено преобразование вида 2.

3. Пусть система (5.10) несовместна. Тогда система (5.11) также несовместна. Действительно, предположим, что система (5.11) совместна и имеет решение К=(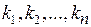). Тогда из доказанного выше следует, что К=(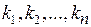) является решением системы (5.10), что противоречит условию. Значит, система (5.11) тоже несовместна. ■

Для преобразований вида 2 докажите утверждение теоремы самостоятельно.

Элементарным преобразованиям системы (5.9) соответствуют определенные преобразования строк ее расширенной матрицы 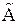, и наоборот. Действительно, изменению порядка уравнений в системе соответствует изменение порядка строк в расширенной матрице. Умножению уравнения на число соответствует умножение на это число строки расширенной матрицы. Прибавлению к одному уравнению системы другого уравнения, умноженного на любое число, соответствует прибавление к одной строке расширенной матрицы другой строки, умноженной на это число. Вычеркивание нулевого уравнения соответствует вычеркиванию нулевой строки матрицы. Поэтому для упрощения записи будем преобразовывать не саму систему (5.9), а строки ее расширенной матрицы .

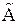Приведем с помощью элементарных преобразований расширенную матрицу системы (5.9) к ступенчатому виду

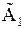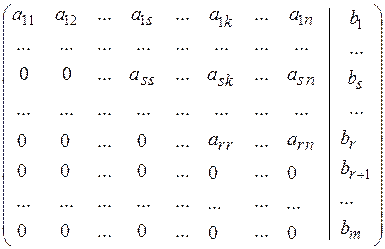= (5.12)

Если рассмотренную последовательность элементарных преобразований провести над теми же уравнениями системы (5.9) с расширенной матрицей 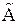, то придем к эквивалентной системе уравнений с расширенной матрицей :

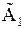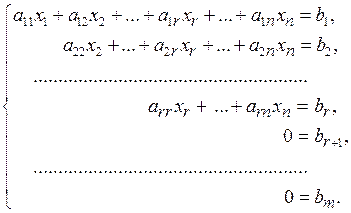(5.13)

Не ограничивая общности, мы можем предположить, что
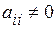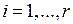, (общий случай сводится к этому случаю посредством перестановки в системе (5.13) соответствующих уравнений и неизвестных).

Ранг основной матрицы системы (5.13) равен r, ранг расширенной матрицы системы не превосходит m. Возможны следующие случаи:

1. Хотя бы одно из значений 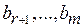не равно нулю.

Тогда 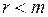и по теореме Кронекера-Капелли система (5.13) несовместна (последние 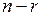уравнений системы противоречивы).

2. Все значения 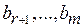равны нулю: 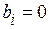при 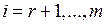. Последние 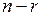уравнений системы (5.13) являются тождествами 0=0 и их можно вычеркнуть из системы. В этом случае ранги основной и расширенной матриц системы (5.13) равны r и по теореме Кронекера-Капелли система совместна, причем .

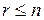1) Пусть число уравнений системы (5.13) равно числу переменных,
т.е. 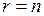. Тогда расширенная матрица 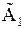системы (5.13) является квадратной матрицей порядка n. Эта матрица имеет треугольный вид, следовательно, 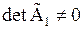и по теореме 5.2 система имеет единственное решение. Система (5.13) принимает вид

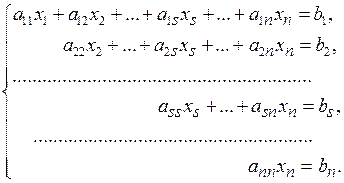(5.14)

Из последнего уравнения этой системы найдем единственное значение 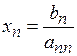. Подставляя найденное значение 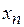в предпоследнее уравнение системы (5.14), получим единственное значение 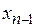и так далее. Наконец, из первого уравнения системы получим единственное значение 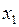. Таким образом, система (5.14) является определенной, определенной будет и эквивалентная ей система (5.9), и имеет единственное решение ().

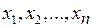2) Пусть теперь число уравнений системы (5.13) меньше числа неизвестных, т.е. 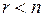. Запишем систему (5.13) следующим образом:

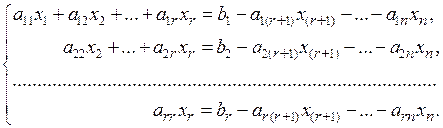(5.15)

Нулевые уравнения в системе отброшены.

Неизвестные 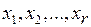, стоящие в левых частях уравнений, называются главными (базисными) неизвестными. Оставшиеся 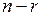неизвестные (стоящие в правых частях уравнений системы (5.15)) называются свободными неизвестными.

Придадим свободным неизвестным произвольные значения:

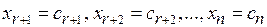(5.16)

и подставим их в уравнения системы (5.15). Получившаяся система имеет невырожденную квадратную матрицу порядка 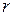, а значит,
по теореме 5.2 система имеет единственное решение, соответствующее данному набору свободных неизвестных (5.16). Так как произвольные наборы значений для свободных неизвестных можно выбрать бесконечным числом способов, то получим бесконечное множество решений системы (5.15). Следовательно, эквивалентная ей система (5.9) является неопределенной. Решение системы (5.15), в котором все 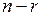свободных неизвестных равны нулю, называется базисным.

Таким образом, система, содержащая меньше уравнений, чем неизвестных, либо несовместна, либо неопределенна.

Переход от системы (5.9) к равносильной ей системе (5.13) с помощью элементарных преобразований называется прямым ходом метода Гаусса, а нахождение неизвестных из системы (5.13) – обратным ходом.

Пример. Исследовать на совместность систему уравнений

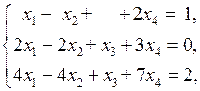
и решить ее в случае совместности.

○ Приведем матрицу системы с помощью элементарных преобразований к ступенчатому виду.

~~~.

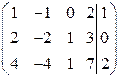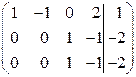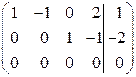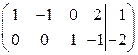Ранги основной и расширенной матриц системы равны 2, число неизвестных равно 4, значит система совместная, неопределенная. Число базисных неизвестных 2, число свободных неизвестных 2. Выпишем все возможные группы базисных неизвестных: 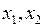; ; 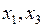; ; 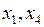; 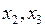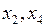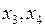. Группу 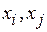, , 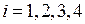, 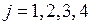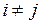можно выбрать в качестве базисных неизвестных, если определитель матрицы ступенчатого вида из коэффициентов при этих неизвестных не равен нулю. Рассмотрим первую группу 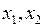. Определитель матрицы ступенчатого вида из коэффициентов при этих неизвестных 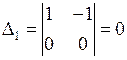, значит, эти неизвестные не могут быть базисными. Вычислим последовательно остальные определители: , , , , .

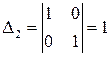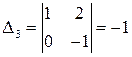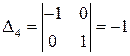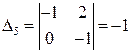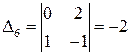Все определители, кроме 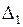, отличны от нуля, значит, соответствующие пары неизвестных можно выбирать в качестве базисных. Найдем первое базисное решение, взяв в качестве базисных неизвестных 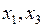, а в качестве свободных – неизвестные 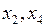. Приравняем к нулю свободные неизвестные: 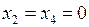и получим систему уравнений в виде: 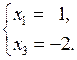Таким образом, первое базисное решение (1; 0; –2; 0).

Если в качестве базисных неизвестных взять 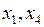и приравнять к нулю соответствующие свободные неизвестные 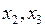, т.е. 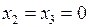, то получим систему в виде: 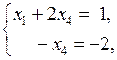откуда 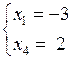. Тогда второе базисное решение (–3; 0; 0; 2). Аналогично можно найти остальные базисные решения (0; –1; –2; 0), (0; 3; 0; 2), (0; 0; 0,5; –1,5).

Найдем теперь общее решение системы, при этом в качестве базисных неизвестных возьмем 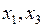. Перепишем систему в виде:

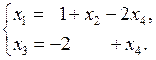
Здесь базисные неизвестные 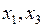выражены через свободные неизвестные 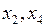. Общее решение запишется в виде:

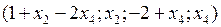. (5.17)

Придавая свободным неизвестным произвольные значения получим бесконечное множество решений системы. Общее решение (5.17) содержит все возможные решения системы, в том числе при 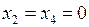имеем полученное выше первое базисное решение. ●