Формальная постановка задачи

Чтобы привести формальную постановку МЗН, введем сле­дующие понятия, термины и обозначения. Имеются два исход­ных множества по n элементов: С{ n } и O { n }. Обозначим: C { C 1, C 2, …, C i, …, C n } – первое множество, элементы которого назовем субъектами; O { O 1, O 2, …, O j, …, O n } – второе множество, элементы которого назовем объектами.

Имеется множество из N критериев оценки субъектов и объектов. Каждая оценка на шкале критерия имеет две форму­лировки, отражая взаимные требования и возможности элемен­тов двух множеств (см. пример далее). Шкалы критериев – по­рядковые, с небольшим, как правило, числом оценок, упоря­доченных от лучшей к худшей. Лучшая оценка имеет ранг, равный единице. Оценки могут быть как словесные, так и чис­ленные. (Заметим, что шкалы словесных оценок наиболее ха­рактерны для МЗН. Иллюстрацией могут служить приведенные выше примеры.)

Часть критериев отражает требования субъектов и возмож­ности объектов, другая часть – требования объектов и возмож­ности субъектов. Введем следующие обозначения: S k { S 1, S 2, …, S m, …, S w } – множество оценок на шкале k -го критерия; 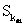– m -я по порядку оценка на шкале k -го критерия; 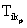– р-я по порядку оценка на шкале требований i -г o элемента по k -му критерию; 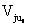– t -я оценка на шкале возможностей j -г o эле­мента по u -му критерию.

Назовем критериальным соответствием (КС) различие по одному из критериев между требованиями субъекта (объекта) и возможностями объекта (субъекта). Требования i -г o элемента по k -му критерию (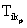) удовлетворены возможностями j -г o эле­мента по k -му критерию (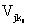), если р > t. При этом критери­альное соответствие идеально.

Назовем назначением любую пару { C i, O j }, образованную дву­мя элементами, принадлежащими разным исходным множествам. Имеется множество из (n? n) назначений { C i, O j }, i, j = 1, 2,..., n, для двух исходных множеств по n элементов: C { n } и O { n }.

Идеальным назначением назовем пару { C i, O j }, для которой взаимные требования полностью удовлетворены по всем крите­риям, т.е. все КС идеальны.

Назовем решением многокритериальной задачи о назначе­ниях единичную диагональную матрицу MS (n? n), диагональные элементы которой соответствуют назначениям, формирующим решение. Заметим, что количество возможных решений для размерности исходных множеств С{ n } и O { n } равно n!, что и вы­зывает (в общем случае) существенные трудности при решении МЗН большой размерности.

Идеальным решением назовем решение МЗН, все назначе­ния которого идеальны.

Предположим, что назначения могут быть проранжированы, т. е. каждому возможному назначению может быть присво­ен ранг, отражающий его качество, с точки зрения ЛПР. Тогда любое решение МЗН может быть охарактеризовано совокупно­стью рангов отдельных назначений, сформировавших решение. Теперь можно записать МЗН в следующем виде.

Дано: два множества: C i (i =1,2,..., п) и O j (j =1, 2,..., n); оценка каждого элемента двух множеств по N критериям (k 1, k 2, …, k N).

Требуется: на основе предпочтения ЛПР определить и вы­брать из множества эффективных решений такое, для которого сумма рангов лучших S назначений (S? n) минимальна.

В исследовании операций известна задача о назначениях с одним критерием качества решения [4]. В однокритериальной задаче о назначениях задана стоимость образования той или иной пары, например исполнения каждой из работ каждым из исполнителей. Задан также критерий – минимум стоимости вы­полнения всей совокупности работ. Для решения однокритери­альной задачи применяются различные методы, как правило, ос­нованные на алгоритмах дискретного программирования. Далее мы будем использовать однокритериальную задачу о назначени­ях как вспомогательное средство при решении существенно более сложной многокритериальной задачи. МЗН занимает промежу­точное положение между задачами принятия индивидуальных и коллективных решений. Действительно, ЛПР стремится най­ти наибольшее число максимально удовлетворенных субъектов и объектов, основываясь на характеристиках, отражающих ин­тересы и индивидуальные предпочтения субъектов и объектов. Но в ситуациях, требующих выбора, ЛПР руководствуется своими предпочтениями.

Впервые близкая по постановке задача была сформулиро­вана в [5]. В ней используется тот же критерий оптимальности и дан алгоритм решения задач малой размерности. Его приме­нение позволило решить практическую задачу [2].