2014-02-12
412
Пусть теперь две точки заданы в пространстве
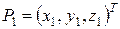и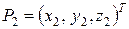 
(7.30)
Тогда уравнение прямой, проходящей через эти точки будет иметь вид:
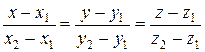. (37.1)
И в параметрической форме
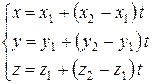(7.32)
Уравнения (32), как и ранее, можно представить в компактной форме
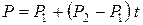(7.33)
Рассмотрим задачу о пересечении плоскости отрезком прямой.
Условие задачи. В декартовой системе координат заданы плоскость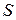 
, определяемая уравнением
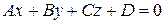(7.34)
и отрезок прямой 
, где точки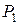 
и 
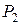определяются по (30).
Определить: пересекает отрезок плоскость 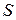(рис. 3) или нет (рис. 4).
 
| 
| ||
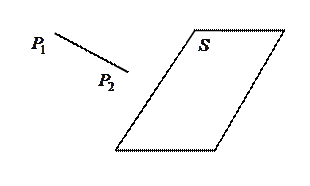
| Рис. 7.4 | Рис. 7.5 |
Для решения поставленной задачи определим значение параметра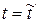 
, при котором прямая (7.32) и плоскость (7.34) имеют общую точку.
Подставляя выражения для координат (7.32) в уравнение плоскости (7.34) и вводя обозначения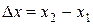 
, 
, 
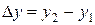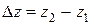, получим
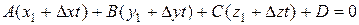(7.35)
Из (7.35) получаем
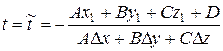(7.36)
для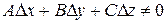 
.
Тогда если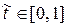 
, то отрезок пересекает плоскость 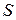. В противном случае плоскость 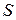пересекает продолжение рассматриваемого отрезка.
Координаты точки пересечения определяются путем подстановки значения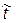 
в (7.32)
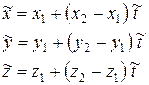, (7.37)
или в компактной форме
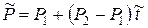(7.38)
Рассмотрим случай, когда
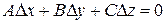(7.39)
Известно, что в уравнении плоскости коэффициенты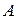 
, 
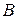и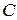 
являются координатами вектора 
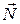, нормального к этой плоскости, т.е. 
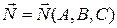. Рассмотрим вектор 
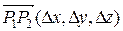, построенный на отрезке . Тогда условие (7.39) означает что
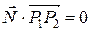(7.40)
Равенство нулю скалярного произведения (7.40) означает, что вектор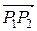 
перпендикулярен вектору нормали 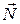и, следовательно, параллелен плоскости 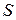. Если при этом также справедливо равенство 
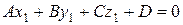, то вектор 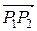(отрезок ) лежит в плоскости .
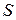Рассмотрим один частный случай рассмотренной задачи, когда плоскость (7.34) параллельна плоскости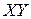 
и определяется уравнением 
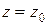или
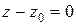(7.41)
В этом случае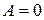 
, 
, 
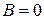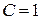и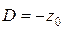 
. Подставляя эти значения в (7.36), получаем
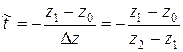(7.42)
Подставив найденное значение 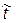в (37), находим
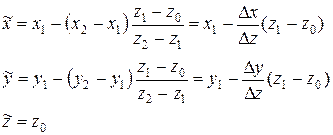(7.43)
Рассмотренная задача возникает при построении линий уровня (см. ниже).
