Уравнение прямой на плоскости

Пусть в декартовой системе координат на плоскости 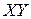заданы две точк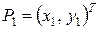и

и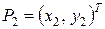

Тогда уравнение прямой, проходящей через эти точки имеет вид:

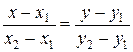(7.20)

Пологая в (7.20)

,

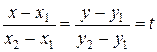получаем параметрическое уравнение прямой на плоскости, проходящей через точк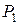и и .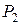

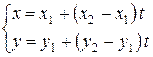, (7.21)

Пусть

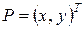
Тогда (21) можно записать в виде

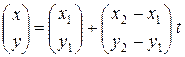, (7.22)

или в более компактной форме

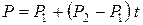(7.23)

Из (7.23) следует, что при 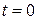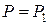, а при 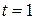получаем, что .

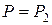Таким образом, при 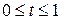точка 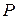принадлежит отрезку .

Следовательно, при 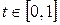, уравнение (7.23) можно считать уравнением отрезка .

Рассмотрим задачу о взаимном расположении двух отрезков на плоскости.

Условие задачи. На плоскости заданы два отрезка прямой: 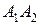и

,

,

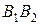
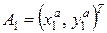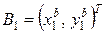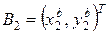
Определить: пересекаются или нет отрезк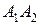и и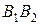

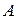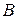Запишем уравнения прямых и , определяемых отрезкам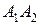ии 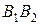соответственно в параметрической форме

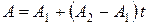(7.24)

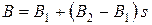(7.25)

Предположим, что прямые пересекаются и 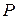точка из пересечения

В этой точке справедливо равенство

Или

Отсюда

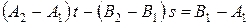
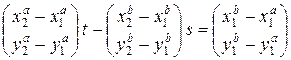
или

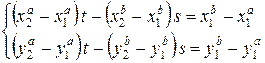(7.26)

Определитель системы (26) равен

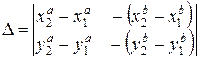(7.27)

Если 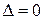, то система уравнений (7.26) решения не имеет: отрезки параллельны (или накладываются).

Если 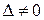, то система уравнений (7.26) имеет единственное решение 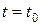и .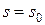

При этом есл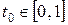и и 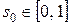, то отрезки пересекаются, иначе пересекаются их продолжения, или один отрезок пересекается с продолжением другого.

Подставляя найденные значения 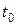и 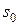в (7.24) или в (7.25), можно определить координаты точки пересечения отрезков .

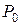(7.28)

или

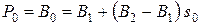(7.29)