Конечные и бесконечные множества

В теории конечных множеств справедливо утверждение: «часть меньше целого».

Пример 5. А = {1,2,3,4,5}, В ={1,2,3}, B Í A и B ¹ A.

Нельзя установить взаимно-однозначное соответствие между конечным множеством и его собственным подмножеством.

def. Множество А называется конечным, если оно не равномощно никакому собственному подмножеству. В противном случае множество называется бесконечным.

def. Бесконечным называется множество, из которого можно выделить равномощное ему собственное подмножество.

Пример 6. Рассмотрим множества N и A ={ x Î N | x - четное число}, А Í N, A ¹ N. Между N и А можно установить взаимно однозначное соответствие:

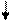
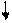
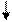
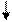N: 1 2 3... n...

A: 2 4 6... 2 n...

Таким образом, в теории бесконечных множеств теряет силу утверждение, что «часть меньше целого».

def. Кардинальное число называется конечным, если оно является мощностью конечного множества.

def. Конечные ненулевые кардинальные числа называются натуральными числами. Другими словами, натуральное число – это общее свойство класса конечных непустых равномощных множеств.

Наименьшей бесконечной мощностью является À₀ - мощность множества натуральных чисел. À₀ = | N | (алеф нуль).

def. Множества, равномощные множеству натуральных чисел называют

счётными.

То есть множество является счётным, если его элементы можно перенумеровать.

Пример 7. Z @ N. Докажем это.

Если мы попробуем нумеровать множество Z по порядку, начиная с какого-нибудь места, то никогда эту нумерацию не закончим. Поэтому все числа до выбранного места останутся незанумерованными.

..., -n,..., -3, -2, -1, 0, 1, 2, 3,..., n,...

Иными словами, все положительные числа и нуль нумеруются нечетными числами, а все отрицательные целые числа - четными.

Пример 8. Q @ N. Докажем это.

Выпишем сначала все положительные дроби со знаменателем 1, потом все положительные дроби со знаменателем 2, потом со знаменателем 3 и т.д. У нас получается таблица следующего вида:

Ясно, что в этой таблице, мы встретим любое положительное рациональное число, и при этом ни один раз. Например, число 3 встретится и в виде дроби 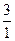, и в виде дроби 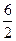, и в виде дроби .

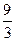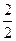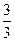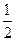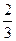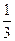Нумеруем по квадратам. При нумерации некоторые дроби будем пропускать. Например, так как получает уже №1, то дроби , и т.д. пропускаем: они выражают то же самое число. Получается следующая нумерация: 1, 2, , 3, , , , 4, , , ,...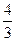

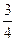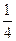Мы занумеровали все положительные рациональные числа. А теперь уже легко понять, как нумеруются все (то есть положительные и отрицательные) рациональные числа. Для этого надо записать их отдельно в виде двух таблиц и числа одной таблицы нумеровать чётными номерами, а второй – нечетными и еще оставить один номер для нуля.