Критерий Пирсона

Критерий Пирсона для проверки гипотезы о виде закона распределения случайной величины. Проверка гипотез о нормальном, показательном и равномерном распреде-лениях по критерию Пирсона. Критерий Колмогорова. Приближенный метод проверки нормальности распределения, связанный с оценками коэффициентов асимметрии и эксцесса.

В предыдущей лекции рассматривались гипотезы, в которых закон распределения генеральной совокупности предполагался известным. Теперь займемся проверкой гипотез о предполагаемом законе неизвестного распределения, то есть будем проверять нулевую гипотезу о том, что генеральная совокупность распределена по некоторому известному закону. Обычно статистические критерии для проверки таких гипотез называются критериями согласия.

Достоинством критерия Пирсона является его универсальность: с его помощью можно проверять гипотезы о различных законах распределения.

1. Проверка гипотезы о нормальном распределении.

Пусть получена выборка достаточно большого объема п с большим количеством различ-ных значений вариант. Доя удобства ее обработки разделим интервал от наименьшего до наибольшего из значений вариант на s равных частей и будем считать, что значения вари

ант, попавших в каждый интервал, приближенно равны числу, задающему середину интервала. Подсчитав число вариант, попавших в каждый интервал, составим так называемую сгруппированную выборку:

варианты х ₁ х ₂  х_s

частоты  п ₁ п ₂  п_s,

где х_i – значения середин интервалов, а п_i – число вариант, попавших в i -й интервал (эмпи-рические частоты).

По полученным данным можно вычислить выборочное среднее 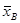 и выборочное среднее квадратическое отклонение σ_В. Проверим предположение, что генеральная совокупность распределена по нормальному закону с параметрами M (X) = 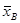, D (X) = 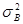. Тогда можно найти количество чисел из выборки объема п, которое должно оказаться в каждом интер-вале при этом предположении (то есть теоретические частоты). Для этого по таблице значений функции Лапласа найдем вероятность попадания в i -й интервал:

,

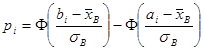где а_i и b_i - границы i -го интервала. Умножив полученные вероятности на объем выборки п, найдем теоретические частоты: п_i =n?p_i. Наша цель – сравнить эмпирические и теоретические частоты, которые, конечно, отличаются друг от друга, и выяснить, являются ли эти различия несущественными, не опровергающими гипотезу о нормальном распределении исследуемой случайной величины, или они настолько велики, что противоречат этой гипотезе. Для этого используется критерий в виде случайной величины

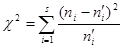. (20.1)

Смысл ее очевиден: суммируются части, которые квадраты отклонений эмпирических частот от теоретических составляют от соответствующих теоретических частот. Можно доказать, что вне зависимости от реального закона распределения генеральной совокупно-сти закон распределения случайной величины (20.1) при 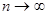 стремится к закону распределения  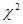(см. лекцию 12) с числом степеней свободы k = s – 1 – r, где r – число параметров предполагаемого распределения, оцененных по данным выборки. Нормальное распределение характеризуется двумя параметрами, поэтому k = s – 3. Для выбранного критерия строится правосторонняя критическая область, определяемая условием

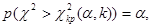(20.2)

где α – уровень значимости. Следовательно, критическая область задается неравенством 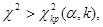 а область принятия гипотезы - .

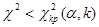Итак, для проверки нулевой гипотезы Н ₀: генеральная совокупность распределена нормально – нужно вычислить по выборке наблюдаемое значение критерия:

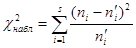, (20.1`)

а по таблице критических точек распределения χ² найти критическую точку 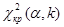, используя известные значения α и k = s – 3. Если  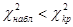- нулевую гипотезу принимают, при  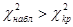ее отвергают.

2. Проверка гипотезы о равномерном распределении.

При использовании критерия Пирсона для проверки гипотезы о равномерном распределе-нии генеральной совокупности с предполагаемой плотностью вероятности

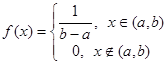
необходимо, вычислив по имеющейся выборке значение 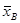, оценить параметры а и b по формулам:

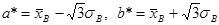, (20.3)

где а* и b* - оценки а и b. Действительно, для равномерного распределения М (Х) = 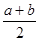, , 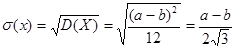откуда можно получить систему для определения а* и b *: 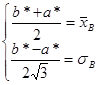, решением которой являются выражения (20.3).

Затем, предполагая, что 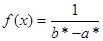, можно найти теоретические частоты по формулам

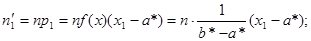
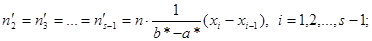
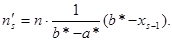
Здесь s – число интервалов, на которые разбита выборка.

Наблюдаемое значение критерия Пирсона вычисляется по формуле (20.1`), а критическое – по таблице с учетом того, что число степеней свободы k = s – 3. После этого границы критической области определяются так же, как и для проверки гипотезы о нормальном распределении.

3. Проверка гипотезы о показательном распределении.

В этом случае, разбив имеющуюся выборку на равные по длине интервалы, рассмотрим последовательность вариант 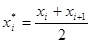, равноотстоящих друг от друга (считаем, что все варианты, попавшие в i – й интервал, принимают значение, совпадающее с его серединой), и соответствующих им частот n_i (число вариант выборки, попавших в i – й интервал). Вычислим по этим данным  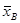и примем в качестве оценки параметра λ величину 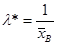. Тогда теоретические частоты вычисляются по формуле

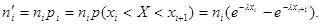
Затем сравниваются наблюдаемое и критическое значение критерия Пирсона с учетом того, что число степеней свободы k = s – 2.