Продуктивность модели Леонтьева полностью определяется величиной собственного числа λA матрицы А коэффициентов прямых затрат.
Теорема 3. Модель Леонтьева (2.1) продуктивна тогда и только тогда, когда λA < 1. Достаточность. Поскольку AX = λAX, то 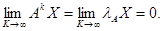 Учитывая, что X>0,
Учитывая, что X>0, 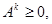 получаем, что
получаем, что 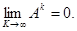
Рассмотрим равенство 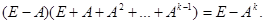
Поскольку предел при k → ∞ правой части существует, то существует предел и левой части, т. е. 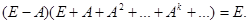
Этим доказано, что ряд 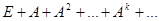 сходится, а матрица E – А невырождена. Получаем формулу суммы геометрической прогрессии:
сходится, а матрица E – А невырождена. Получаем формулу суммы геометрической прогрессии:
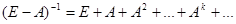
Поскольку Аk ≥ 0, k = 1, 2,..., то 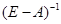 ≥ 0, из чего непосредственно вытекает, что для любого вектора конечного спроса Y ≥ 0 существует неотрицательное решение системы уравнений (2.3):
≥ 0, из чего непосредственно вытекает, что для любого вектора конечного спроса Y ≥ 0 существует неотрицательное решение системы уравнений (2.3):
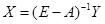 , (2.14)
, (2.14)
что и означает продуктивность модели Леонтьева.
Необходимость. Пусть модель Леонтьева продуктивна. Возьмем в качестве вектора КП Y в уравнении (2.1) произвольный положительный вектор Y > 0. По предположению о продуктивности существует вектор X ≥ 0 такой, что
X – АXT = Y, т.е. X > АXT ≥ 0. Умножая последнее неравенство скалярно на вектор строку цен pA > 0, имеем pA X > pA АXT = pA λAXT. Поскольку pAXT>0, получаем λA< 1. Теорема доказана.
Теорема 3 дает возможность проверять модель Леонтьева на продуктивность, однако ее формулировка абстрактна и далека от экономических интерпретаций. Сформулируем без доказательства достаточный признак продуктивности модели Леонтьева, наиболее удобный для проверки продуктивности матрицы межотраслевого баланса в натурально-стоимостной форме.
Если матрица А неотрицательна и неразложима, сумма элементов каждой строки не больше 1 и хотя бы для одной строки строго меньше 1, то модель Леонтьева, определяемая матрицей А, продуктивна.
Если матрица А неотрицательна и неразложима, сумма элементов каждой строки не больше 1 и хотя бы для одной строки строго меньше 1, то модель Леонтьева, определяемая матрицей А, продуктивна.
Очевидно, что условие ri ≤ 1, i == 1, 2,..., п, весьма естественно – оно означает, что i -я отрасль способна удовлетворить запросы всех отраслей. Вместе с тем простые примеры показывают, что одного этого условия недостаточно; так, матрица 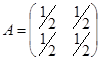 не является продуктивной.
не является продуктивной.
Таким образом, если модель Леонтьева продуктивна, то вектор валового выпуска, который необходим для удовлетворения конечного спроса Y, определяется формулой (2.14).
 2014-02-13
2014-02-13 3622
3622








