Покажем достаточность. Пусть 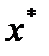 - оптимальное решение задачи (1)-(3) и предположим, что
- оптимальное решение задачи (1)-(3) и предположим, что 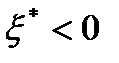 . Тогда
. Тогда 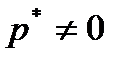 . Рассмотрим вектор
. Рассмотрим вектор 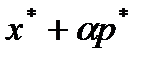 и выберем значение
и выберем значение 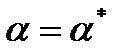 следующим образом. Если
следующим образом. Если 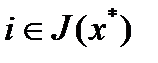 , то
, то 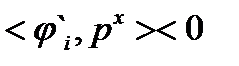 . Следовательно,
. Следовательно, 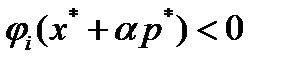 при всех
при всех 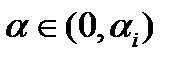 для достаточно малого
для достаточно малого 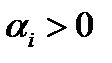 . Если
. Если 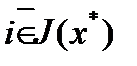 , то есть
, то есть 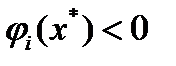 , то в силу непрерывности функции
, то в силу непрерывности функции 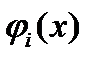 неравенство
неравенство 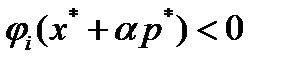 сохранится при всех
сохранится при всех 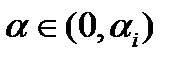 для достаточно малого
для достаточно малого 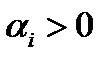 .
.
Положим 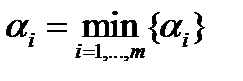 . Тогда для любого
. Тогда для любого 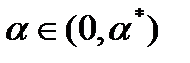 вектор
вектор 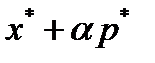 является допустимым решением задачи (1)-(3). Из условия
является допустимым решением задачи (1)-(3). Из условия 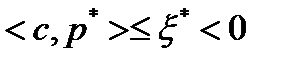 получим
получим 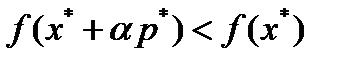 , при
, при 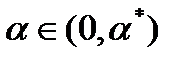 , что оптимальности
, что оптимальности 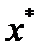 .
.
Докажем необходимость. Пусть 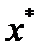 не является оптимальным решением задачи (1)-(3). Тогда существует
не является оптимальным решением задачи (1)-(3). Тогда существует 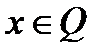 , для которого
, для которого 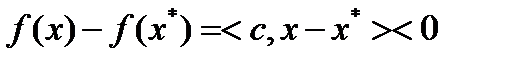 . Пусть
. Пусть 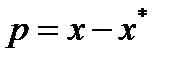 . Тогда
. Тогда 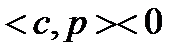 . Если
. Если 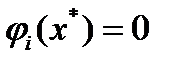 , то есть
, то есть 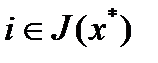 , то из неравенства для гладких выпуклых функций
, то из неравенства для гладких выпуклых функций 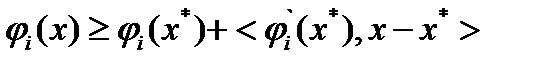 получим
получим 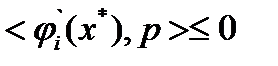 (12)
(12)
Из условия Слейтеда следует существование вектора 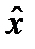 , для которого
, для которого 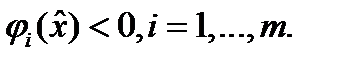 Пусть
Пусть 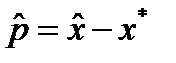 . Если
. Если 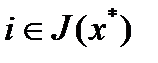 , то аналогично (12) имеем
, то аналогично (12) имеем 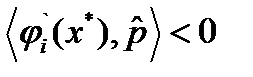 .Выберем
.Выберем 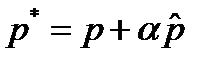 . Тогда при достаточно малом
. Тогда при достаточно малом 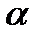 справедливо
справедливо 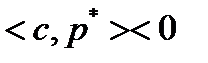 и
и 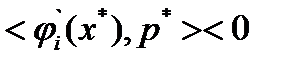 для
для 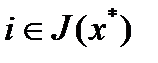 . Отсюда непосредственно вытекает, что
. Отсюда непосредственно вытекает, что 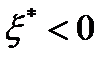 ч. т. д.
ч. т. д.
Если в решении 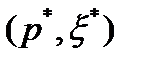 задачи (8)-(11) величина
задачи (8)-(11) величина 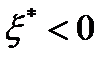 мала по абсолютно величине, то это может привести к замедлению скорости сходимости метода возможных направлений. Чтобы избежать этих трудностей, следует изменить множество номеров
мала по абсолютно величине, то это может привести к замедлению скорости сходимости метода возможных направлений. Чтобы избежать этих трудностей, следует изменить множество номеров 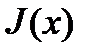 в ограничении (10). Опишем один из таких подходов, в котором используется следующее множество номеров
в ограничении (10). Опишем один из таких подходов, в котором используется следующее множество номеров 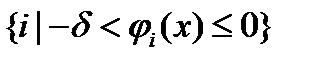 , где
, где 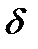 положительное число. Другими словами, это множество номеров ограничений задачи (1)-(3), которые в точке
положительное число. Другими словами, это множество номеров ограничений задачи (1)-(3), которые в точке 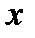 выполняются как равенства с точностью до
выполняются как равенства с точностью до 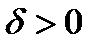 .
.
|
|
|
Путь 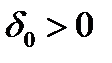 и
и 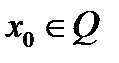 некоторое начальное приближение. Допустим, что известно
некоторое начальное приближение. Допустим, что известно 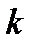 -е приближение
-е приближение  и
и 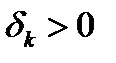 . Введем множество номеров
. Введем множество номеров 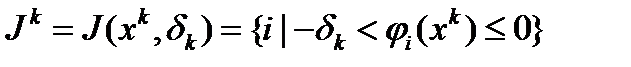 ,
, 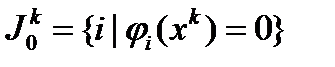 .
.
Рассмотрим следующую задачу линейного программирования:
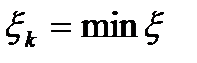 (13),
(13), 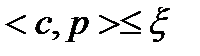 (14),
(14), 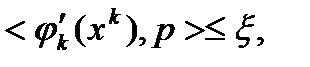 для всех
для всех 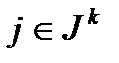 (15),
(15), 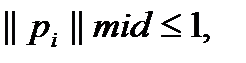 для всех
для всех 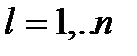 (16). Обозначим эту задачу
(16). Обозначим эту задачу 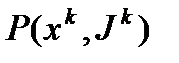 . Приведем описание одной итерации метода возможных направлений. Пусть
. Приведем описание одной итерации метода возможных направлений. Пусть 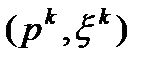 оптимальное решение задачи
оптимальное решение задачи 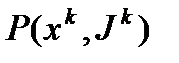 . Рассмотрим три случая:
. Рассмотрим три случая:
1) если 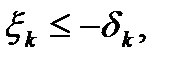 то полагая
то полагая 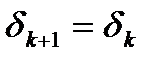 .
.
2) если 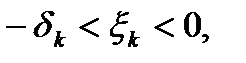 то полагая
то полагая 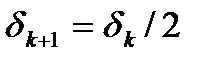 .
.
3) если 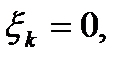 то найдем решение
то найдем решение 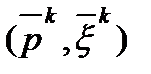 задачи
задачи  .
.
При 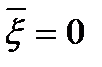 вектор
вектор 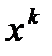 согласно критерию оптимальности является оптимальным решением задачи (1)-(3). Если же
согласно критерию оптимальности является оптимальным решением задачи (1)-(3). Если же 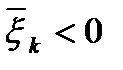 , то полагаем
, то полагаем 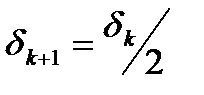 ,
, 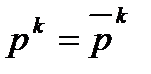 .
.
Как уже упоминалось выше, в случае 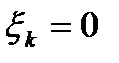 нельзя утверждать, что вектор
нельзя утверждать, что вектор 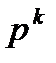 является направлением спуска. Поэтому, решив задачу
является направлением спуска. Поэтому, решив задачу  на основании теоремы1 можно оценить оптимально или нет текущее приближение
на основании теоремы1 можно оценить оптимально или нет текущее приближение 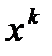 . Если
. Если 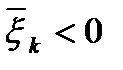 , то в качестве направления спуска выбирается вектор
, то в качестве направления спуска выбирается вектор 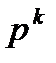 . Длина шага
. Длина шага 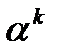 определяется по следующей схеме. Пусть
определяется по следующей схеме. Пусть 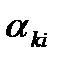 наименьший положительный корень уравнения
наименьший положительный корень уравнения 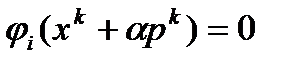 . Тогда полагаем
. Тогда полагаем 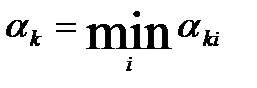 и
и 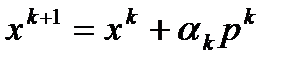 ,
, 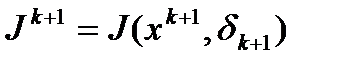 .
.
Теорема 1. Пусть 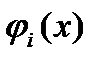 гладкие выпуклые функции, выполнено условие Слейтера и множество Q ограничено. Тогда
гладкие выпуклые функции, выполнено условие Слейтера и множество Q ограничено. Тогда
1) последовательность 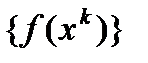 сходится к величине
сходится к величине 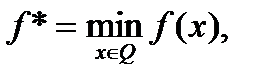 т.е.
т.е. 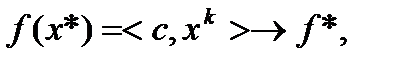 при
при 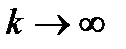 ;
;
2) любая предельная точка 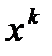 последовательности
последовательности 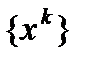 есть точка минимума функции
есть точка минимума функции 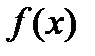 на множестве допустимых решений Q.
на множестве допустимых решений Q.
Доказательство. По построению последовательность 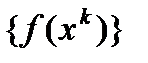 не возрастающая и, в виду ограниченности множества Q, сущ. предел
не возрастающая и, в виду ограниченности множества Q, сущ. предел 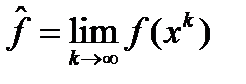 и
и 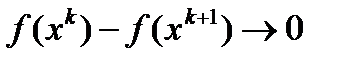 при
при 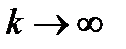 (1)
(1)
|
|
|
Величина 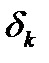 на каждом шаге либо делится пополам, либо остается без изменений. Покажем, что
на каждом шаге либо делится пополам, либо остается без изменений. Покажем, что 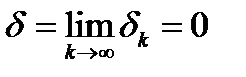 . Предположим противное, т.е.
. Предположим противное, т.е.  . Тогда найдется
. Тогда найдется 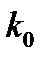 такое, что
такое, что 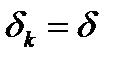 и
и 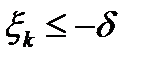 для всех
для всех 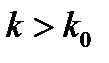 . Другими словами, начиная с номера
. Другими словами, начиная с номера 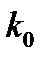 в алгоритме всегда реализуется первый случай
в алгоритме всегда реализуется первый случай 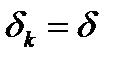 . Выберем некоторую сходящуюся подпоследовательность
. Выберем некоторую сходящуюся подпоследовательность 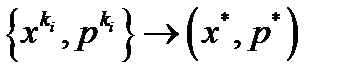 . Такая подпоследовательность существует в виду ограниченности множества
. Такая подпоследовательность существует в виду ограниченности множества  и условия нормировки (16) (п.9.1). Пусть
и условия нормировки (16) (п.9.1). Пусть 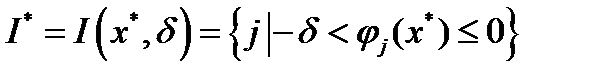 . Тогда при некотором
. Тогда при некотором 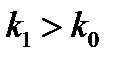 для всех
для всех 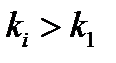 справедливо
справедливо 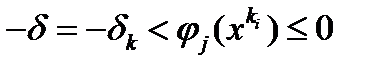 для
для 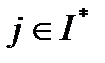 . Это означает, что
. Это означает, что 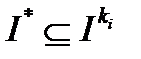 для достаточно больших
для достаточно больших 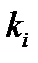 . Следовательно,
. Следовательно, 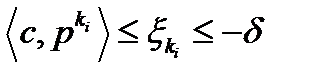 ,
, 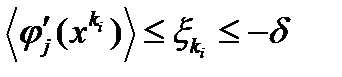 , для
, для 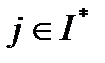 . Тогда из непрерывности функций
. Тогда из непрерывности функций 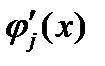 следует
следует 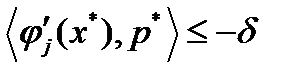 для
для 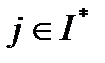 . С другой стороны,
. С другой стороны, 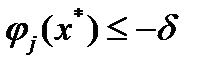 для
для 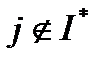 . Отсюда вытекает существование
. Отсюда вытекает существование 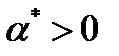 такое, что
такое, что 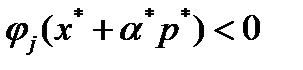 для всех
для всех 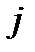 . С учетом непрерывности функций
. С учетом непрерывности функций 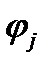 это означает, что
это означает, что 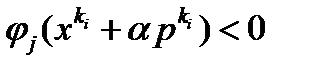 для достаточно больших
для достаточно больших 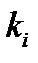 и всех
и всех 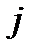 . Таким образом, отсюда следует, что
. Таким образом, отсюда следует, что 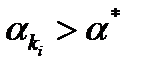 . Тогда
. Тогда 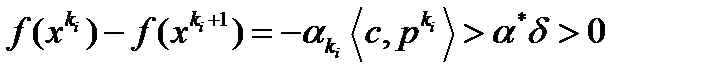 , что противоречит (1). Следовательно,
, что противоречит (1). Следовательно, 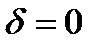 .
.
Покажем, что 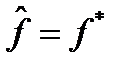 . Пусть
. Пусть 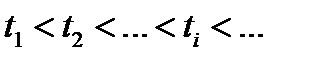 номера тех итераций, когда происходит дробление величины
номера тех итераций, когда происходит дробление величины 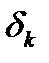 . Из неравенства
. Из неравенства 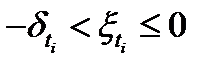 следует, что
следует, что 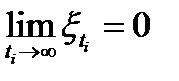 . Можно считать, что
. Можно считать, что 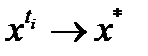 . Пусть
. Пусть 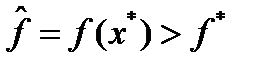 . Тогда из критерия оптимальности следует, что существуют
. Тогда из критерия оптимальности следует, что существуют 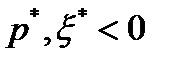 такие, что
такие, что 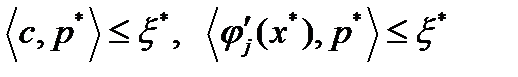 для
для 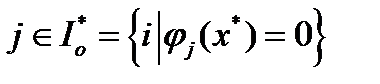 . С другой стороны, найдется
. С другой стороны, найдется 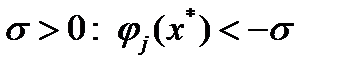 для всех
для всех 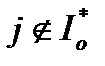 . Из непрерывности дифференцируемости функций
. Из непрерывности дифференцируемости функций 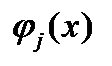 следует, что найдется номер
следует, что найдется номер 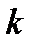 такой, что для всех
такой, что для всех 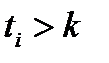
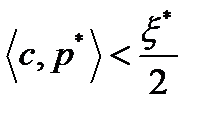 (2),
(2), 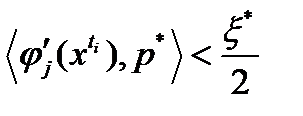 для всех
для всех 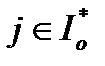 (3),
(3), 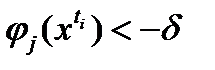 , для всех
, для всех 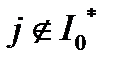 . (4) Кроме того, из сходимости к 0 последовательности
. (4) Кроме того, из сходимости к 0 последовательности 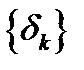 следует неравенство
следует неравенство 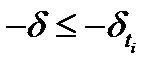 для достаточно больших
для достаточно больших 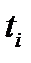 . Из последнего неравенства и неравенства (4) имеем
. Из последнего неравенства и неравенства (4) имеем 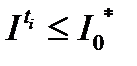 для всех
для всех 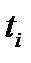 больших некоторого
больших некоторого 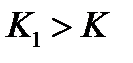 . Отсюда, с учетом неравенств (2), (3) и выбора
. Отсюда, с учетом неравенств (2), (3) и выбора 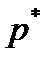 , получаем
, получаем 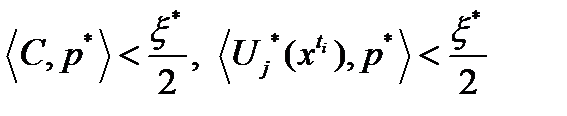 для всех
для всех 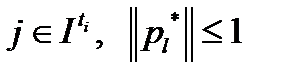 для всех
для всех 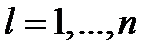 . Таким образом,
. Таким образом, 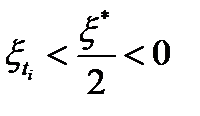 , для любого
, для любого 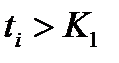 , что противоречит сходимости последовательности
, что противоречит сходимости последовательности 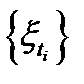 к нулю. Следовательно,
к нулю. Следовательно, 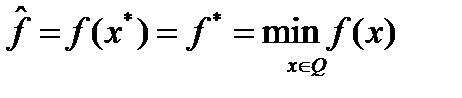 . Поскольку
. Поскольку 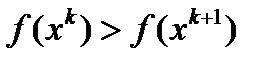 , то для любой предельной точки
, то для любой предельной точки 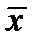 последовательности
последовательности 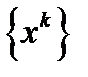 имеет место равенство
имеет место равенство 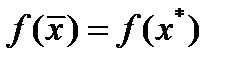 . ч.т.д.
. ч.т.д.
 2015-01-21
2015-01-21 373
373