Теорема. Пусть u = f (х, у) задана в области D и пусть х = х(t) и у = у(t) определены в области 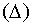 , причём, когда
, причём, когда 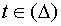 , то х и у принадлежат области D. Пусть функция u дифференцируема в точке M 0(x 0, y 0, z 0), а функции х (t) и у (t) дифференцируемы в соответствующей точке t 0, то сложная функция u = f [ x (t), y (t)] =F (t) дифференцируема в точке t 0 и имеет место равенство:
, то х и у принадлежат области D. Пусть функция u дифференцируема в точке M 0(x 0, y 0, z 0), а функции х (t) и у (t) дифференцируемы в соответствующей точке t 0, то сложная функция u = f [ x (t), y (t)] =F (t) дифференцируема в точке t 0 и имеет место равенство:
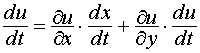 .
.
Доказательство. Так как u дифференцируема по условию в точке (x 0, y 0), то её полное приращение представляется в виде
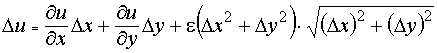 .
.
Разделив это соотношение на 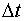 , получим:
, получим:
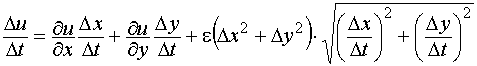 .
.
Перейдём к пределу при 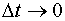 и получим формулу
и получим формулу
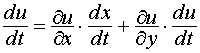 .
.
Замечание 1. Если u = u (x, y) и x = x, y = y (x), то полная производная функции u по переменной х
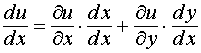 или
или 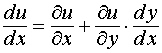 .
.
Последнее равенство можно использовать для доказательства правила дифференцирования функции одной переменной, заданной неявно в виде F (x, y) = 0, где y = y (x) (см. тему № 3 и пример 14).
Имеем: 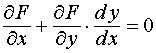 . Отсюда
. Отсюда 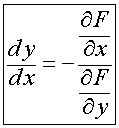 . (6.1)
. (6.1)
Вернёмся к примеру 14 темы № 3:
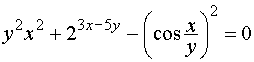 ;
;
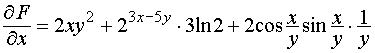 ;
;
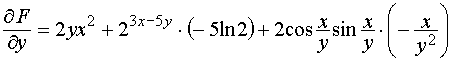 ;
;
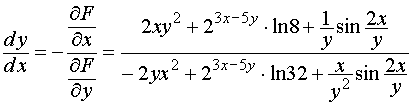 .
.
Как видим, ответы совпали.
Замечание 2. Пусть u = f (х, у), где х = х (t, v), у = у (t, v). Тогда u есть в конечном счёте сложная функция двух переменных t и v. Если теперь функция u дифференцируема в точке M 0 (x 0, y 0), а функции х и у дифференцируемы в соответствующей точке (t 0, v 0), то можно говорить о частных производных по t и v от сложной функции в точке (t 0, v 0). Но если мы говорим о частной производной по t в указанной точке, то вторая переменная v считается постоянной и равной v 0. Следовательно, речь идёт о производной только от сложной функции по t и, следовательно, мы можем воспользоваться выведенной формулой. Таким образом, получим:
|
|
|
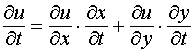 и
и 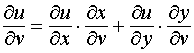 .
.
Пример 13. Найти полную производную функции u = x y,где x = sin t, y = cos t.
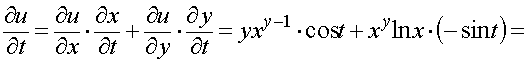
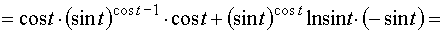
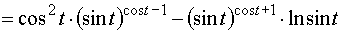 .
.
 2015-01-21
2015-01-21 10625
10625
