Интегральная теорема Муавра-Лапласа

Теорема Муавра-Лапласа является следствием центральной предельной теоремы.

Теорема Пусть имеется n независимых испытаний, в каждом из которых событие А появляется с вероятностью p, то при n ® ¥ имеет место соотношение:

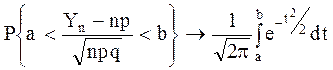(1)

где Y_n - число появлений события А в n опытах; q=1-p.

Доказательство: Выведем формулу (1) как следствие ЦПТ. Обозначим , тогда утверждение теоремы равносильно тому, что

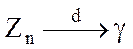~N(0,1)

"Нормированная" случайная величина Z_n связанная с Y_n линейной зависимостью, дискретна. Также дискретна и случайная величина Y_n, распределенная по биномиальному закону, но при большом n (n®¥) ее значения расположены на оси абсцисс так тесно, что можно ее рассматривать как непрерывную, с плотностью распределения f(z). Математическое ожидание случайной величины Y_n M[Y_n]=np, дисперсия D[Y_n]=npq, случайная величина Y_n имеет биномиальное распределение с параметрами n, p. Найдем числовые характеристики случайной величины Z_n как математическое ожидание и дисперсию линейной функции от случайной величины Y_n. Имеем:

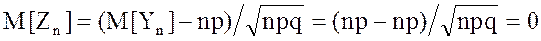
D[Z_n]=1; s[Z_n]=1

Таким образом, случайная величина Z_n имеет числовые характеристики m=0 и s=1, не зависящие от n.

Учитывая, что 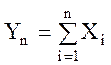, где X_i - индикатор события А в i-ом опыте, убеждаемся, что случайная величина Z_n есть сумма n независимых одинаково распределенных случайных величин. Применяя ЦПТ видим, что при n®¥ случайная величина Z_n имеет распределение, близкое к нормальному с параметрами (m=0 и s=1), откуда следует справедливость формулы (1).