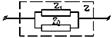
В общем виде типовые элементы электронной автоматики, выполненные на базе операционного усилителя, имеют структуру, показанную на рис. 7.3. На этом рисунке операционный усилитель (ОУ) имеет внешние цепи с комплексным сопротивлением z 0 и z 1, причем z 1 – сопротивление на входе элемента, а z 0 – сопротивление цепи обратной связи.
Сопротивления z 0 и z 1 комплексные, т.к. в общем случае содержат, кроме резисторов с активным сопротивлением, емкостные и индуктивные элементы цепей с соответствующими реактивными сопротивлениями. Именно поэтому расчет схем на базе операционных усилителей удобно выполнять в комплексной форме с использованием преобразования Лапласа.
Комплексные сопротивления отдельных элементов электронных цепей приведены в табл. 7.1 (позиции 1–3). Там же приведены выражения для полных комплексных сопротивлений при параллельном (позиция 4) и последовательном (позиция 5) соединении элементов с комплексными сопротивлениями z 1 и z 2.
Таблица 7.1
| № | Элемент цепи | Комплексное сопротивление |

| Z (p) = R | |
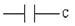
| 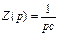
| |
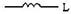
| Z (p) = pl | |
| 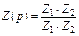
| |

| Z (p) = Z1 + Z2 |
Пользуясь приведенными в табл. 7.1 соотношениями, можно определить полное комплексное сопротивление любой электронной цепи и рассчитать, в частности, сопротивления Z0 и Z1 схемы, показанной на рис. 7.3. Для этого вместо каждого электронного элемента цепи записывается его комплексное сопротивление в соответствии с позициями 1–3, табл. 7.1, а полное сопротивление рассчитывается в соответствии с позициями 4–5.
Рассчитав сопротивления Z 0 и Z 1, определяют передаточную функцию W (p) звена по следующей формуле:
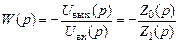 . (7.1)
. (7.1)
Рис. 7.1. Схемы звеньев САР на базе операционного усилителя
Варианты схем САР приведены на рис. 7.2:
Знак «–» в формуле (7.1) ставится тогда, когда операционный усилитель является инвертирующим, т.е. его выходное напряжение имеет противоположный знак по отношению ко входному. Это условие выполняется практически наиболее часто. Когда же выходное сопротивление неинвертировано – знак «–» опускается.
Дальнейший путь расчета и исследования электронных схем автоматики – приведение выражения (7.1) к виду
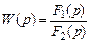 ,
,
где 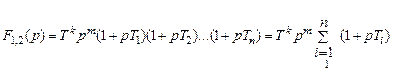 .
.
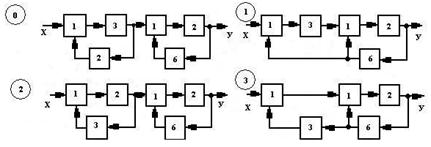


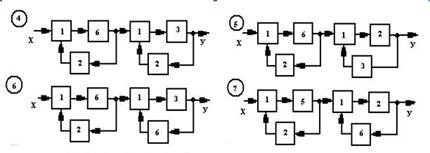
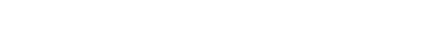
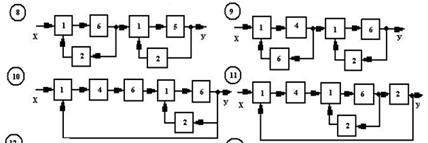

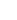
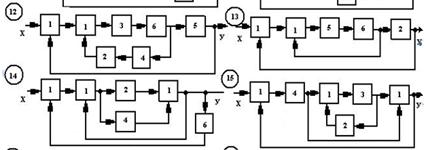
Рис. 7.2. Варианты схем систем автоматического регулирования


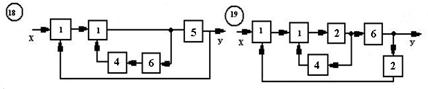
Окончание рис. 7.2
Затем определяют известными из теории автоматического управления методами характеристики САР, влияющие на эффективность и качество ее функционирования.
на практике часто встречаются типовые динамические звенья (табл. 7.2), описываемые дифференциальными уравнениями не выше второго порядка.
Для улучшения характеристик в электронные системы автоматического управления (САУ) вводят обратные связи, которые обеспечивают воздействие выходного сигнала на входной. Для этого может быть использован сумматор (звено 1 на рис. 7.1), на вход которого поступают входной сигнал и сигнал обратной связи. Если сигнал обратной связи является неинвертированным, или синфазным, по отношению к входному сигналу, то образуется положительная обратная, связь, так как указанные сигналы суммируются с одинаковыми знаками, а если инвертированным – то отрицательная.
Например, в варианте 0 на рис. 7.2 к сумматору подводится сигнал обратной связи, сформированный при прохождении через нечетное количество инвертирующих усилителей. Обратная связь в таком случае является отрицательной. Отрицательная (ООС) и положительная (ПОС) обратная связь на структурных схемах изображается следующими знаками соответственно:
 – для ООС
– для ООС  – для ПОС.
– для ПОС.
После определения вида обратной связи расчеты проводят по выражениям (7.4) или (7.5), но уже без учета инвертирования входящими ОУ, т.е. по модулю.
Приведем пример начального расчета задания для звена на базе ОУ, показанного на рис. 7.3.
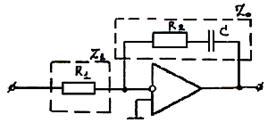
Рис. 7.3. Пример звена для расчета
Определим передаточную функцию:
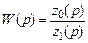 .
.
Комплексное сопротивление 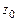 определим в соответствие с табл. 7.1. (позиции 1, 2, 5):
определим в соответствие с табл. 7.1. (позиции 1, 2, 5):
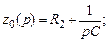
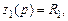
где 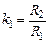 ,
, 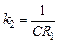 .
.
Полученная передаточная функция является суммой передаточных функций типового безынерционного звена (табл. 7.2, позиция 1) и идеального интегратора (табл. 7.2, позиция 5).
После определения передаточных функций, всех звеньев в варианте задания и вида обратных связей составляют структурную схему. На рис. 7.4 показана составленная для примера структурная схема.
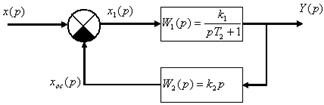
Рис. 7.4. Пример представления структурной схемы
Таблица 7.2
Типовые динамические значения
| № п/п | Тип звена | Вид передаточной функции | Вид дифференциального уравнения |
| Безынерционное | 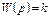
| 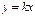
| |
| Апериодическое 1 порядка | 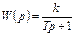
| 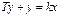
| |
| Апериодическое 2 порядка | 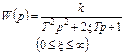
| 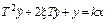
| |
| Колебательное | 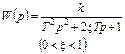
| 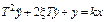
| |
| Идеальное интегрирующее | 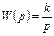
| 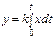
| |
| Инерционное интегрирующее | 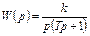
| 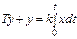
| |
| Идеальное дифференцирущее | 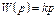
| 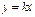
| |
| Инерционное дифференцирущее | 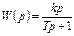
| 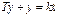
|
Передаточная функция всей системы  определяется с учетом соединений ее звеньев по следующим правилам:
определяется с учетом соединений ее звеньев по следующим правилам:
при последовательном соединении звеньев
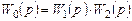 ; (7.2)
; (7.2)
при параллельном соединении звеньев
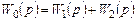 ; (7.3)
; (7.3)
при отрицательной обратной связи
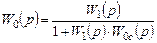 ; (7.4)
; (7.4)
при положительной обратной связи
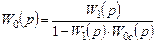 . (7.5)
. (7.5)
Определим, например, передаточную функцию системы, показанной на рис. 7.4. Пользуясь выражением для соединения с отрицательной обратной связью (7.4), получим
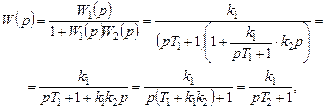
где 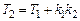 .
.
Для определения частотных характеристик системы переходят от передаточной функции W(p) к комплексной частотной передаточной функции W (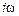 ) путем формальной замены переменной
) путем формальной замены переменной 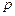 на
на
(i · ω), где = 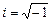 .
.
Далее выделяют в функции W (i ω), вещественную часть и мнимую, содержащую 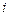 :
:
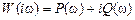 ,
,
где 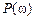 и
и 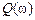 – вещественная и мнимая частотная характеристики, соответственно.
– вещественная и мнимая частотная характеристики, соответственно.
Например, для рассматриваемого примера находим частотную передаточную функцию и ее вещественную и мнимую части:
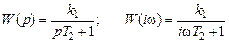 ;
;
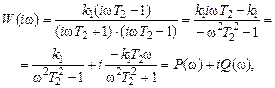
где 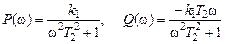 . (7.6)
. (7.6)
При преобразованиях знаменатель и числитель домножались на комплексное выражение (комплексное число), сопряженное знаменателю, и учитывалось, что
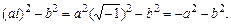
Амплитудно-фазовая характеристика (АФХ) строится на комплексной плоскости в координатах P (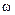 ) и i
) и i 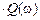 для различных значений циклической частоты
для различных значений циклической частоты 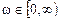 .
.
Например, АФХ (годограф) показана на рис. 7.5.
Зависимость от частоты отношения амплитуды выходного сигнала к амплитуде входного называется амплитудно-частотной характеристикой (АЧХ). Для ее построения необходимо найти модуль комплексной частотной характеристики W (i ω):
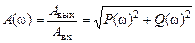 . (7.7)
. (7.7)
Зависимость от частоты фазового сдвига, получаемого сигналом после прохождения на выход, называется фазочастотной характеристикой (ФЧХ). Для ее построения находят аргумент комплексной частотной функции:
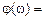 arctg
arctg 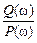 . (7.8)
. (7.8)
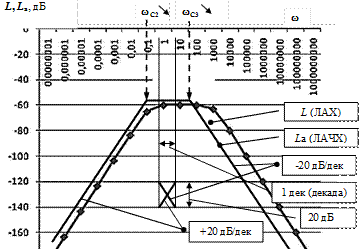
Рис. 7.5. Построение ЛАЧХ
Продолжим расчет рассматриваемой схемы. По выражениям (7.7), (7.8), используя (7.6), определим АЧХ и ФЧХ:
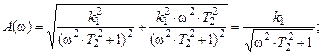
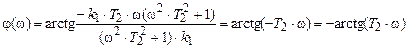 .
.
По результатам расчета строят графики.
Примечание. При расчетах нужно учитывать выражения для постоянной времени:
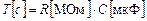 . (7.9)
. (7.9)
Логарифмические характеристики строятся в координатах 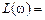
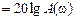 и
и 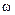 , причем циклическая частота откладывается в логарифмическом масштабе, но с указанием по оси абсцисс численных значений для частоты
, причем циклическая частота откладывается в логарифмическом масштабе, но с указанием по оси абсцисс численных значений для частоты 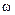 .
.
Следует отметить общую особенность построения графиков логарифмических частотных характеристик: значение 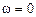 на оси абсцисс находится в (–¥) из-за логарифмического масштаба.
на оси абсцисс находится в (–¥) из-за логарифмического масштаба.
Частоты сопряжения 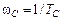 являются характерными точками изменения наклона асимптотической ЛАХ. В каждой из частот сопряжения
являются характерными точками изменения наклона асимптотической ЛАХ. В каждой из частот сопряжения 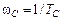 , определяемых исходя из сомножителей
, определяемых исходя из сомножителей 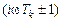 комплексной частотной передаточной функции
комплексной частотной передаточной функции 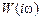 , происходит изменение текущего угла наклона асимптотической ЛАХ на ±20 дБ/дек. Указанной закономерностью пользуются для построения асимптотической ЛАХ, непосредственно по виду передаточной функции
, происходит изменение текущего угла наклона асимптотической ЛАХ на ±20 дБ/дек. Указанной закономерностью пользуются для построения асимптотической ЛАХ, непосредственно по виду передаточной функции 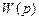 . Это позволяет строить асимптотические ЛАХ без проведения достаточно сложных математических преобразований, ориентируясь лишь на вид передаточной функции.
. Это позволяет строить асимптотические ЛАХ без проведения достаточно сложных математических преобразований, ориентируясь лишь на вид передаточной функции.
Построение переходной характеристики для единичного ступенчатого входного воздействия основано на переходе во временную область от выражения
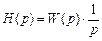 . (7.10)
. (7.10)
Выражение (7.10) описывает выходную величину H(p), когда на вход САР с передаточной функцией W(p) подано единичное ступенчатое воздействие, изображением которого есть 1/ p.
Переходя от выражения (7.10) во временную область, получают выражение для переходной характеристики – реакцию системы на единичное ступенчатое входное воздействие:
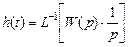 .
.
Знак L 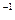 в выражении обозначает обратное преобразование Лапласа.
в выражении обозначает обратное преобразование Лапласа.
Для не очень сложных передаточных функций обратное преобразование осуществляют либо по таблицам обратных преобразований
[2; 22], либо используя формулы обратных преобразований, в частности, разложение Хевисайда [22; c. 234]. Используют также аналитическая разрешение соответствующего дифферинциального уравнения [2].
Построив графически переходную характеристику, определяют время переходного процесса как время входа в зону с указанной погрешностью отклонения δ.
Используем для обратного преобразования Лапласа разложение Хевисайда для рациональных алгебраических функций в случае простых корней [22, c. 234] в виде
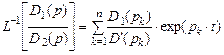 ,
,
где 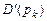 – знаменатель отношения многочленов, в котором опускаются сомножители вида
– знаменатель отношения многочленов, в котором опускаются сомножители вида 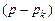 , для значений корней
, для значений корней 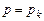 .
.
 2015-01-30
2015-01-30 441
441








