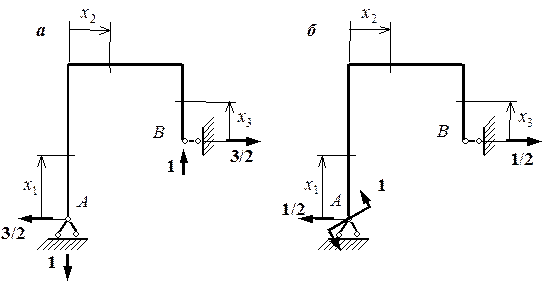Решение

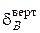Рис. 4.29. Рама под действием единичной обобщенной силы: а – соответствующей ; б – соответствующей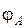

Будем искать первое обобщенное перемещение – вертикальное перемещение точки В. В соответствии с методом Максвелла – Мора для определения этого перемещения приложим в точке В единичную вертикальную сосредоточенную силу (рис. 4.29, а) и найдем изгибающий момент, вызванный этой нагрузкой (координаты 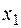, , 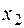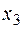должны отсчитываться так же, как при определении момента от заданной нагрузки):

участок 1: 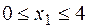м;

;

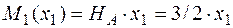участок 2: 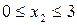м;

;

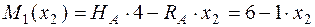участок 3: 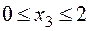м;

.

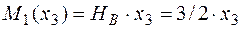Аналогично для определения второго обобщенного перемещения – угла поворота сечения А – приложим в точке А сосредоточенную пару сил, равную единице (рис. 4.29, б), и определим изгибающий момент от этой пары:

участок 1: 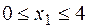м;

;

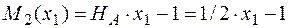участок 2: 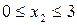м;

;

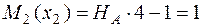участок 3: 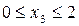м;

.

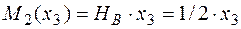Вариант 1. Аналитическое интегрирование формулы

Максвелла – Мора

Подставим в формулу Максвелла – Мора (4.21) выражения для изгибающих моментов от заданной нагрузки, найденные ранее при определении внутренних усилий в рассматриваемой раме, умножим их на выражения для изгибающих моментов от единичных обобщенных сил на всех трех участках и выполним интегрирование. Тогда, учтя, что 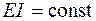, проинтегрируем формулу (4.21):

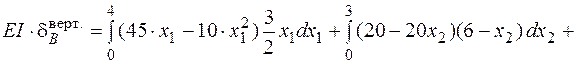
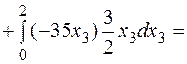250 кН·м³;

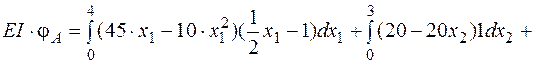
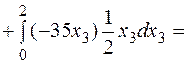–63,3 кН·м².

В соответствии с правилом знаков метода Максвелла – Мора положительный знак вертикального перемещения говорит о том, что точка В перемещается по направлению обобщенной силы, то есть вверх. Сечение А поворачивается по часовой стрелке (в сторону, противоположную направлению единичной пары сил, так как знак угла поворота отрицательный).

Вариант 2. Интегрирование формулы Максвелла – Мора с помощью правила Верещагина

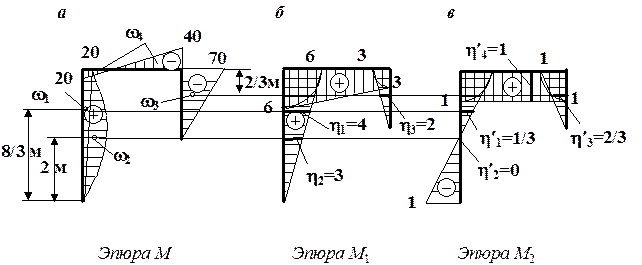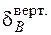Рис. 4.30. Эпюры моментов: а – от заданной нагрузки; б – от единичной обобщенной силы, соответствующей ; в – от единичной обобщенной силы, соответствующей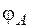

Построим эпюры моментов от заданной нагрузки М и от единичных обобщенных сил, соответствующих искомым перемещениям, М ₁ и М ₂ (рис. 4.30). Для перемножения эпюр разобьем эпюру М на 4 простые фигуры: два треугольника w₁ и w₃, сегмент w₂ и трапецию w₄. Найдем ординаты под центрами тяжести этих фигур на эпюре М ₁ (h₁, h₂ и h₃ на рис. 4.30, б). Эпюру М на ригеле, имеющую форму трапеции w₄ с основаниями разного знака, умножаем на трапецию эпюры М ₁ по правилу трапеций (4.24). Согласно правилу Верещагина

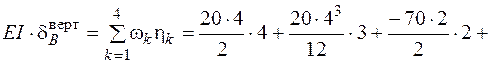
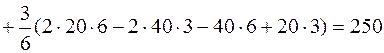кН·м³.

Аналогично находим угол поворота сечения А, перемножая эпюры М и М ₂. Ординаты под центрами тяжести площадей w₁, w₂ и w₃ показаны на рис. 4.30, в (h¢₁, h¢₂ и h¢₃). Для перемножения трапеции w₄ на прямоугольник эпюры М ₂ нет необходимости пользоваться правилом трапеций, так как, где бы ни находился центр тяжести трапеции, значение h¢₄ известно (ординаты на эпюре М ₂ на этом участке постоянны).

Рис. 4.31. Изогнутая ось рамы

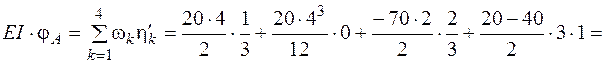
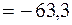кН·м².

Результаты, полученные по двум вариантам использования формулы Максвелла – Мора, совпадают.

В заключение построим деформированную ось рамы так, чтобы она удовлетворяла эпюре изгибающих моментов и условиям закрепления рамы (рис. 4.31). На рис. 4.31 показаны полученные перемещения – 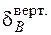, 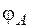в соответствии с их направлениями. Точка перегиба (крестик) изогнутой оси ригеля имеет место в сечении, где меняет знак изгибающий момент. Углы рамы в процессе деформации не меняются.[11]

.
4.3. РАСЧЕТ СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫХ БАЛОК И РАМ

Рекомендуемая литература

Александров А. В., Потапов В. Д., Державин Б. П. Сопротивление материалов. М.: Высш. шк., 1995. Гл. 9 (§ 9.1–9.3).

Гастев В. А. Краткий курс сопротивления материалов. М.: Физматгиз, 1977. Гл. 9.

Дарков А. В., Шпиро Г. С. Сопротивление материалов. М.: Высш. шк., 1989. Гл. 12 (§ 12.1–12.6).