Регрессионные модели параметров

При управлении качеством желательно знать не только зависи­мость друг от друга двух или нескольких количественных призна­ков, но и вид связи между ними и насколько тесна эта связь. Решение этого вопроса имеет большое значение для контроля и управления качеством объекта.

Связь между двумя количественными признаками проявляется в виде определенной тенденции, например, если один признак уве­личивается, то другой увеличивается или уменьшается.

Учитывая, что при статистических связях каждому фиксирован­ному значению одного признака соответствует распределение дру­гого признака, можно представить эту связь в виде зависимости среднего арифметического значения одного признака, например, параметра качества Y от другого признака (признаков, факторов) х. Корреляционная связь, рассмотренная ранее в разделе 3.4, Y с х выражается в общем виде следующим уравнением:

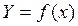(4.1)

Уравнение (4.1) называют модельным уравнением регрессии Y на х. Вид функции f(x) в этих уравнениях зависит от формы связи рассматриваемых признаков. Уравнение регрессии отображает форму связи и дает ответ на вопрос, является ли корреляционная связь прямоли­нейной или криволинейной.

На практике связь между двумя признаками в интересующей области может быть линейной или приблизительной линейной. В тех случаях, когда она нелинейная, часто путем преобразования (логарифмированием, извлечением корня и т. а.) одного из призна­ков можно произвести линеаризацию характера кривой. Кроме того, практически любая нелинейная зависимость может быть раз­делена на участки с линейной зависимостью рассматриваемых признаков. «Наилучшая» прямая, выравнивающая опытные данные, определяется методом наименьших квадратов.

Если наблюдаемые значения признаков обозначить через (x₁, y₁), (x₂, y₂), …, (x_n, y_n), то прямая регрессии Y на х запишется в виде

(4.2)

где - cреднее арифметическое значений y₁, y₂, …, y_n; 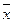— среднее арифметическое значений x₁, х₂,.... x_п; Y определяет ординаты точек вычисленной прямой в зависимости от значений признака.

Коэффициент b в уравнении (4.2) называют коэффициентом регрессии Y на х и определяют по формуле

(4.3)

Коэффициент регрессии Y на х равен тангенсу угла между прямой регрессии и осью x(tga),

Помимо (3.6) коэффициент корреляции может быть записан в следующем виде:

(4.4)

При оценке самого коэффициента корреляции учитывается число пар наблюдений n, по которым было произведено его вычисление. При небольшом числе пар величина r часто значительно отличается от его действительного значения. Поэтому нужен критерий, который установит, случайно ли отклоняется коэффициент корреляции от нуля или имеется корреляционная связь.

Для этого вычисляют

(4.5)

и оценивают полученное значение t с числом степеней свободы v=n-2. Если t £ t_T (табл.[7]), то корреляция между рассматриваемыми признаками существует.

Так как число наблюдений n ограничено, то на практике возникает вопрос, насколько правомерно в дальнейших инженерных расчетах можно пользоваться полученной оценкой коэффи­циента корреляции.

Для ответа на него выполняют проверку статистической значимости (в дальнейшем просто значимости). Это означает вы­яснение, за счет чего оценка коэффициента корреляции оказалось отличной от нуля: за счет ограниченности числа наблюдений, т.е. случайных причин, либо за счет того, что это объективно имеет место.

Проверку значимости коэффициента корреляции выполня­ют по-разному, в зависимости от числа наблюдений пар парамет­ров. При числе наблюдений n > 50 принимают гипотезу о нормальном распределении оценки r*, поскольку доказано, что при n > 50 эта гипотеза, как правило, работает. Затем строят доверительный интервал, симметричный отно­сительно рассчитанной точечной оценки r*. Для коэффициента корреляции его определяют как

I_g=r*-t_gs_r; r*+t_gs_r (4.6)

где среднее квадратичное отклонение коэффициента кор­реляции, равное

s_r 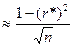(4.7)

t_g — коэффициент, зависящий от доверительной вероятности g. Построив доверительный интервал, проверяют, попадает ли в этот интервал точка

r = 0. Если да, то нет оснований оценку ко­эффициента корреляции считать значимой, ибо отличной от нуля с вероятностью g она оказалась за счет ограниченного числа на­блюдений.

На выходные параметры изделий или техпроцессов оказывают влияние большое число первичных параметров. Часть первичных парамет­ров мы знаем, а о влиянии некоторых из них даже не догадыва­емся. При решении инженерных задач ограничиваются неболь­шим числом наиболее существенных первичных параметров. Обычно это число k £ 5-8. В связи с этим зависимость выходного параметра Y от учитываемых первичных параметров x₁, …, x_k оказывается вероятностной. Тогда корреляционное поле параметров х и Y может, например, принять вид, показанный на рис.3.1.

Проведем в корреляционном поле прямую или кривую линию, которая лучшим образом характеризует из­менение выходного параметра Y в зависимости от первичного па­раметра х. Эту линию называют линией регрессии, а матема­тическое выражение, описывающее линию — уравнением регрессии или регрессионной моделью. Когда первичный параметр не один, а несколько, то говорят об уравнении множественной регрессии.

В инженерной практике популярны регрессионные модели в виде полиномов. Особый интерес представляет полином первой степени. Его математический вид

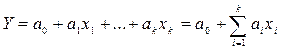(4.8)

где Y— выходной параметр РЭУ или ТП;

x₁,…x_k — первичные параметры;

n— число учитываемых первичных параметров;

a₀,a₁,…,a_k — коэффициенты модели, определяемые по ре­зультатам экспериментов.

Модель вида (4.8) называют также уравнением множествен­ной линейной регрессии.

К математическим моделям предъявляются два основных требования [4]:

простота получения и относительно минимальные погрешности при описании поведения устройства или процесса. Во многом этим требованиям отвечают линейные регрессионные модели вида (4.8). Для определения по данным эксперимента ко­эффициентов a₀, a₁,…a_k могут быть использованы несложные расчетные фор­мулы, а удовлетворительность описания реальных изделий и ТП обу­словлена небольшим отклонением первичных параметров относительно своих средних (номинальных) значений, состав­ляющий обычно не более 20…30%. Из рис. 1.9. вид­но, что замена нели­нейной зависимости на участке x_ном ±Dx прямой линией не вызовет боль­ших ошибок. По этой причине линейные регрессионные модели в боль­шинстве случаев оказываются пригодными для дальнейшего инженерного анализа приборов или ТП их изготовления.

При построении математических моделей возникает вопрос, как в корреляционном поле лучшим образом провести прямую или другую линию. Для ответа на этот вопрос используется метод наименьших квадратов.