Интеграл Фурье

Всякая функция 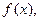которая на отрезке 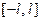удовлет- воряет условиям разложимости в ряд Фурье, может быть на этом отрезке представлена тригонометрическим рядом

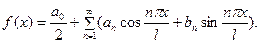(1) Коэффициенты 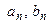ряда (1) вычисляются по формулам

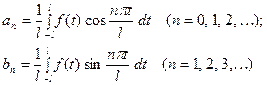(2)

Ряд в правой части равенства (1) можно записать в другой форме. С этой целью внесём в него из формул (2) значения коэффициентов 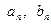, подведём под знаки интегралов 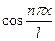и 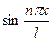(это возможно, поскольку переменной интегрирования является 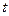) и используем формулу для косинуса разности. Будем иметь:

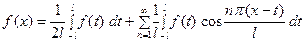. (3)

Если функция первоначально была на интервале числовой оси, большем, чем 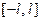(например на всей оси), то разложение (3) воспроизведёт значение этой функции на отрезке 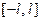и продолжит её на всю числовую прямую, как периодическую функцию, с пери -одом 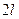. Поэтому, если функция (вообще говоря, непериодическая) определена на всей числовой оси, в формуле (3) можно перейти к пределу при 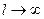. При этом естественно потребовать выполнения следующих условий:

1). удовлетворяет условиям разложимости в ряд Фурье на любом конечном отрезке оси Ох;

2). Функция абсолютно интегрируема на всей чис -ловой оси,

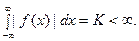(4)

При выполнении условия 2) первое слагаемое правой части равенства (3) при 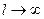стремится у нулю. В самом деле,

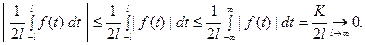
Попытаемся установить, во что перейдёт в пределе при 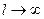сумма в правой части (3). Положим

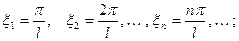
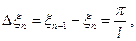
так, что 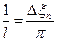. Тогда сумма в правой части (3) примет вид

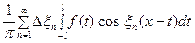. (5)

В силу абсолютной сходимости интеграла, эта сумма, при больших 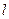, мало отличается от выражения

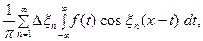
которое напоминает интегральную сумму для функции пере -менного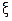

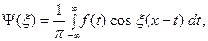
составленную для интервала изменения . Поэтому естественно ожидать, что, при 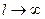, ( 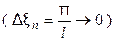сумма (5) перейдёт в интеграл

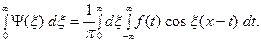
С другой стороны, при 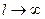( 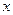фиксировано) из фор -мулы (3) вытекает, что

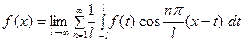, (6)

и мы получаем равенство

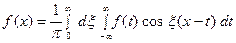. (7)

Достаточное условие справедливости формулы (7) выражается следующей теоремой

ТЕОРЕМА 1. Если функция абсолютно интегрируема на всей числовой оси 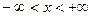и имеет вместе со своей производной конечное число точек разрыва первого рода на любом отрезке 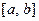, то справедливо равенство

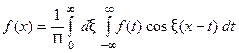
При этом во всякой точке 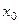, являющейся точкой разрыва 1-го рода функции , значение интеграла в правой части (7) равно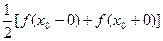

Формулу (7) называют интегральной формулой Фурье, а стоящий в её правой части интеграл - интегралом Фурье. Если воспользоваться формулой для косинуса разности, то формулу (7) можно записать в виде

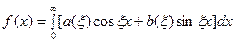, (8) где

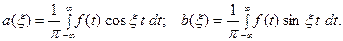(9)

Функции 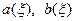являются аналогами соответствующих ко - эффициентов Фурье 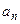и 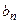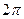- периодической функции, но последние определены для дискретных значений 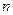, в то время как 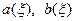определены для непрерывных значений .

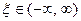2. Комплексная форма интеграла Фурье.

Предполагая абсолютно интегрируемой на всей оси Ох, рассмотрим интеграл

.

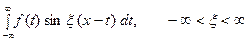Этот интеграл равномерно сходится для 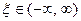, так как 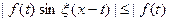и потому представляет собой не- прерывную и, очевидно, нечётную функцию от 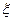. Но тогда 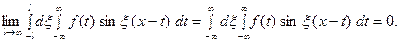С другой стороны, интеграл

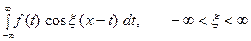
является чётной функцией от переменной 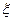, так что 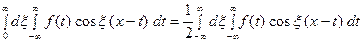Следовательно, интегральную формулу Фурье можно записать так

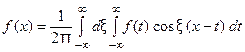. (10)

Умножим равенство

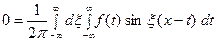
на мнимую единицу 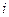и прибавим к равенству (10). Получим 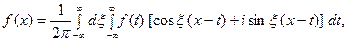Отсюда, в силу формулы Эйлера (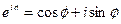), будем иметь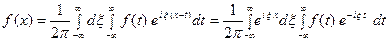

(11) Это комплексная форма интеграла Фурье. Здесь внешнее ин- тегрирование по 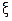понимается в смысле главного значения по Коши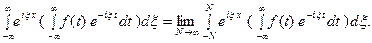

3. Косинус - и синус – преобразования Фурье.

Пусть функция является кусочно гладкой на любом конечном отрезке оси Ох и абсолютно интегрируема на всей оси.

ОПРЕДЕЛЕНИЕ. 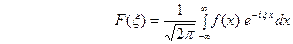(12) называется преобразование Фурье функции (спект- ральной функцией). интегральноеное преобразование функции на интервале с ядром 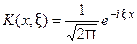. Используя интегральную формулу Фурье

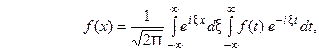Получаем 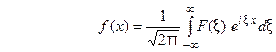(13) это так называемое обратное преобразование Фурье, дающее переход от 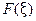к

Иногда прямое преобразование Фурье задают так

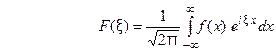(14) Тогда обратное преобразование Фурье определяется форму -лой 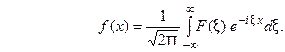(15)

Преобразование Фурье 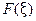функции определяют также следующим образом

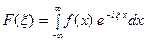. (16) Тогда, в сою очередь,

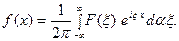(17)

При этом положение множителя 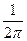достаточно произ- вольно: он может входить либо в формулу (16) либо в формулу (17).

ПРИМЕР 1. Найти преобразование Фурье функции

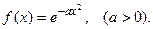
Имеем

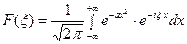(18)

Это равенство допускает дифференцирование по 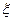под знаком интеграла (получающийся после дифференцирования интеграл равномерно сходится, когда 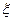принадлежит любому конечному отрезку)

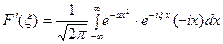. Интегрируя по частям, будем иметь:

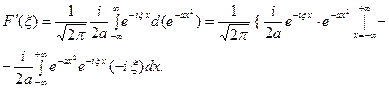Внеинткгральное слагаемое обращается в нуль и мы получа- ем 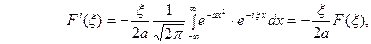Откуда

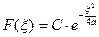(19) (С - постоянная интегрирования). Полагая в (19) 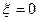, найдём 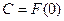. В силу (18), имеем

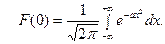
Известно, что 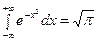. Поэтому 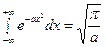и значит 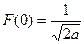. Таким образом, 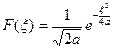. В частности, для 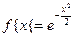, 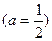получаем, что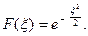

ПРИМЕР 2.. (разряд конденсатора через сопротивление). Рассмотрим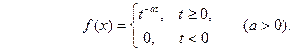

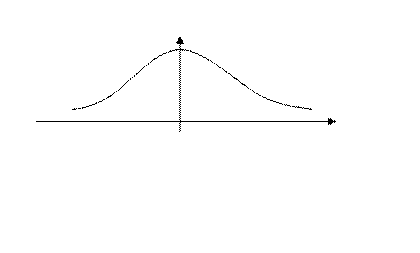Для спектральной функции 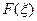получаем 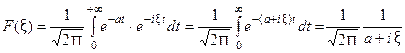Отсюда 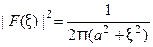, (см. рис. 14).

У

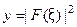
О Х

Рис. 14

Условие абсолютной интегрируемости функции на всей числовой оси является весьма жёстким. Оно исключает, например, такие элементарные функции, как 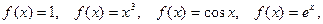для которых преобразования Фурье (в рассматриваемой здесь классической форме) не существует. Фурье – образ имеют только те функции, которые достаточно быстро стремятся к нулю при 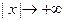(как в примерах 1. и 2.)..

Используя формулу косинуса разности, перепишем интег- ральную формулу Фурье

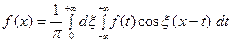в следующем виде:

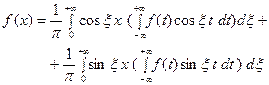(20

Пусть - чётная функция. Тогда

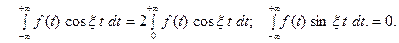
Так что из равенства (20) имеем

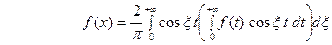. (21) В случае нечётной функции аналогично получаем 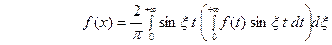. (22)

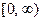Если функция задана лишь на , то формула (21) продолжает на всю ось Ох чётным образом, а формула (22) - нечётным.

ОПРЕДЕЛЕНИЕ. 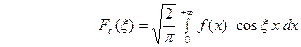(23) (называется косинус – преобразованием Фурье функции .

Из (21) следует, что для чётной функции 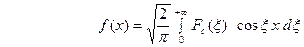. (24) Это означает, что , в свою очередь, является косинус - преобразованием для 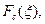Иными словами, функции и 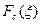являются взаимными косинус – преобразованиями.

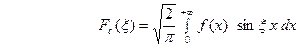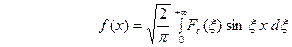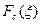ОПРЕДЕЛЕНИЕ . (25) называется синус – преобразованием функции . Из (22) получаем, что для нечётной функции , (26) т.е. и являются взаимными синус – преобразова -ниями.

4, Свойства преобразования Фурье.

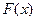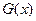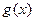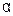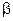1. Линейность. Если и - преобразования Фурье функций и соответственно, то при любых постоянных и преобразованием Фурье функции 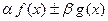является функция .

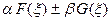Пользуясь свойством линейности интеграла, имеем 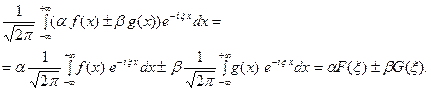Таким образом, преобразование Фурье - это линейный оператор. Обозначив его через 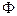, будем писать 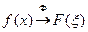или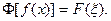

2. Если 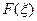- преобразование Фурье абсолютно интегрируемой на всей числовой прямой функции , то 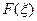ограничено при всех .

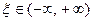В самом деле, пусть функция абсолютно интегрируема на всей оси ,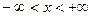

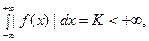
и пусть

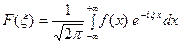- преобразование Фурье функции . Тогда

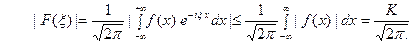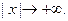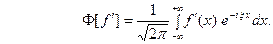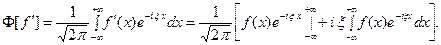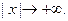3. Преобразование Фурье и операция дифференцирования. Пусть абсолютно интегрируемая функция имеет производную также абсолютно интегрируемую на всей оси Ох, так что стремится к нулю при Считая гладкой функцией, запишем Интегрируя по частям, будем иметь Внеинтегральное слагаемое обращается в ноль, (так как стремится к нулю при ) и мы получаем 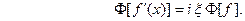(27) Таким образом, дифференцированию функции отвечает умножение её образа Фурье 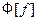на множитель .

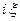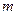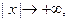Если функция имеет гладкие абсолютно интегрируемые производные до порядка включительно и все они, как и сама функция , стремятся к нулю при то, интегрируя по частям нужное число раз, получим 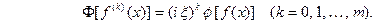(28)

Преобразование Фурье очень полезно именно потому, что оно заменяет операцию дифференцирования операцией умножения на величину 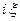и тем самым упрощает задачу интегрирования некоторых видов дифференциальных уравнений.

Так как преобразование Фурье 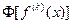абсолютно интегрируемой функции является ограниченной функцией от 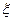(свойство 2), то из соотношения (28) получаем для 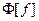следующую оценку:

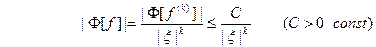Из этой оценки следует: чем больше функция имеет абсолютно интегрируемых производных, тем быстрее её преобразование Фурье стремится к нулю при 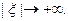Замечание. Условие 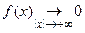является достаточно естественным, поскольку обычная теория интегралов Фурье имеет дело с процессами, которые в том или ином смысле имеют начало и конец, но не продолжаются неограниченно с примерно одинаковой интенсивностью.

5 Связь между скоростью убывания функции при 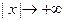и гладкостью её преобразования Фурье.

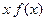Предположим, что не только , но и её произведение являются абсолютно интегрируемыми функциями на всей оси Ох. Тогда преобразование Фурье

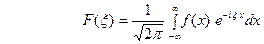функции будет дифференцируемой функцией. Действительно, формальное дифференцирование по параметру 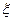подынтегральной функции приводит к интегралу 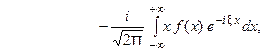который является абсолютно и равномерно сходящимся относительно параметра 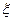. Следовательно, дифференци -рование возможно, и

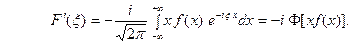Таким образом,

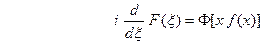, т.е. операция умножения на аргумент 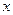переходит после преобразования Фурье в операцию .

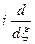Если вместе с функцией абсолютно интегрируемыми на всей числовой прямой Ох являются функции 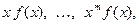то процесс дифференцирования можно продолжить. Получим, что функция 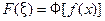имеет производные до порядка 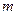включительно, причём 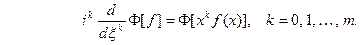Таким образом, чем быстрее функция убывает при 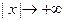, тем более гладкой получается функция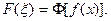

ТЕОРЕМА (о свёртке). Пусть функции 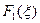и 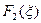- преобразования Фурье функций 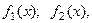соответственно. Тогда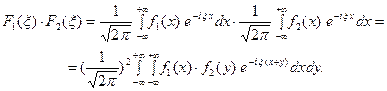

Причём двойной интеграл в правой части сходится абсолютно.

В самом деле, положим 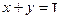, так что 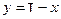. Тогда будем иметь

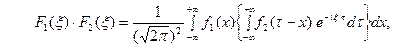или, меняя порядок интегрирования,

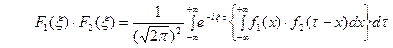. Функция 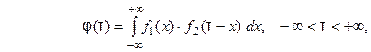называется свёрткой функци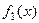й и 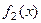, и обозначается символом 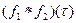. Поэтому можем записать 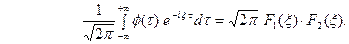Поэтому видим, что преобразование Фурье свёртки функци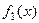й и 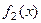равно умноженному на 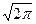произведению преобразований Фурье свёртываемых функций,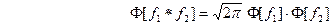

6. Приложения преобразований Фурье.

ПРИМЕР 1. Пусть 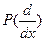- линейный дифферен- циальный оператор порядка 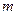с постоянными коэф- фициентами,

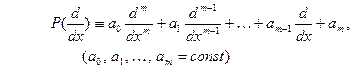
Используя формулу для преобразования Фурье функции

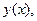находим

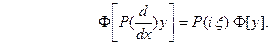Рассмотрим дифференциальное уравнение

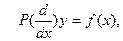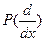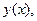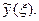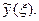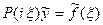(1) где - введённый выше дифференциальный оператор. Предположим, что искомое решение имеет преобразование Фурье Применяя преобразование Фурье к уравнению (1), получим вместо дифференциального алгебраическое уравнение на оси относительно , , откуда 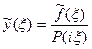, так что формально 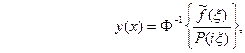где символ 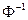обозначает обратное преобразование Фурье.

ПРИМЕР 2 Найти решение 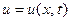уравнения 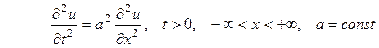(2) при начальных условиях

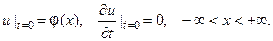(3) Это - задача о свободных колебаниях бесконечной одно -родной струны, когда задано начальное отклонение 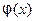точек струны, а начальные скорости отсутствуют.

Поскольку пространственная переменная 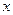изменяется в предедах от 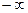до 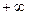, подвергнем уравнение и на- чальные условия преобразованию Фурье по переменной 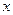. Будем предполагать, что

1) функци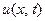и и 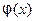- достаточно гладкие и стремятся к нулю при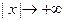 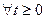настолько быстро, что существуют преобразования Фурье

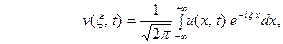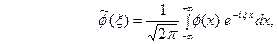(4) (5)

2) допустимы операции дифференцирования, так что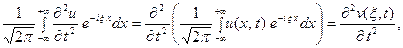

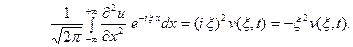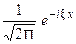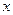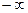(6) (7) Умножая обе части (2) на и интегрируя по от до 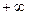, получим:

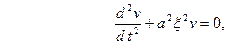(8) а из начальных условий (3) найдём

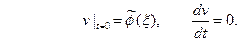(9) Таким образом, применяя к задаче (2) – (3) преобразование Фурье, приходим к задаче Коши (8) – (9) для обыкновенного дифференциального уравнения, где 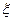- параметр. Решением уравнения (8) является функция

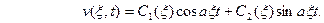Из условий (9) находим, что 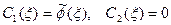, и

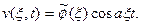Применяя обратное преобразование Фурье, получим 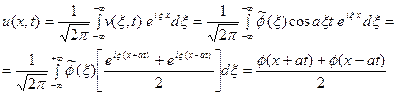Это частный случай формулы Даламбера решения задачи.

ПРИМЕР 3. Преобразование Фурье может быть использовано при решении некоторых интегральных уравнений, т.е. уравнений, в которых неизвестная функция входит под знак интеграла. Рассмотрим, например, уравнение

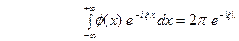(10) где 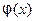- искомая функция. Записав (10) в виде 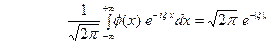(11) замечаем, что левую часть (11) можно рассматривать как преобразование Фурье функции 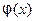, так что (11) равносильно следующему равенству

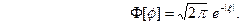Тогда по формуле обращения

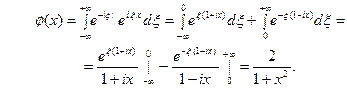Функция 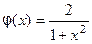является решением уравнения (10).

БИБЛИОГРАФИЧЕСКИЙ СПИСОК

1. Воробьёв Н.Н. Теория рядов. - М.: Наука, 1975.

2. Винер Н. Интеграл Фурье и некоторые его приложения. - М. Физматгиз, 1983.

3. Ефимов А.В. Математический анализ (специальные разделы), ч. 1. – М.: Высш. шк., 1980.

4. Краснов М.Л., Киселёв А.И., Макаренко Г.И., Шикин Е.В., Заляпин В.И., Соболев С.К. Вся высшая математика, т.4, - М.Эдиториал, 2001.

5. Натансон И.П. Краткий курс высшей математики. – Санкт - Петербург, 2001.

6. Харди Г.Х., Рогозинский В.В. Ряды Фурье - М. Физматгиз, 1959.

СОДЕРЖАНИЕ

1. ЭЛЕМЕНТЫ ТЕОРИИ ЧИСЛОВЫХ РЯДОВ

§ 1. Понятие числового ряда ………………………………… 3

§ 2. Числовые ряды с положительными членами

Необходимые и достаточные признаки сходимости … 8

§ 3. Знакопеременные ряды ……………………………………. 19

2. ЭЛЕМЕНТЫ ФУНКЦИОНАЛЬНЫХ РЯДОВ.

§ 1. Определение функционального ряда. …………………. 23

§ 2. Степенные ряды ……………………………………………. 28

§ 3. Ряд Тейлора. Применение степенных рядов

в приближённых вычислениях …………………………. 35

2. РЯДЫ ФУРЬЕ.

§ 1. Вводные замечания. ……………………………………… 42

§ 2. Теорема единственности. Ряд Фурье. ………………... 45

§ 3. Ряд Фурье для чётных и нечётных функций.

Разложение функции, заданной на части

промежутка. Сдвиг основного промежутка …………… 56

§ 4. Ряд Фурье для функции с произвольным

периодом ……………………………………………………. 65

§ 5. Ряд Фурье в комплексной форме …………………….. 70

§ 6. Приложения рядов Фурье. ……………………………… 73

§ 7. Преобразование Фурье. …………………………………… 90

БИБЛИОГРАФИЧЕСКИЙ СПИСОК …………………………….110