Ряды Фурье находят многочисленные применения. Здесь мы покажем, как они используются при решении задачи о колебании струны. Струной называется гибкая нить, не оказывающая сопротивления изгибу.
Рассмотрим струну, которая в начальный момент совмещена с отрезком 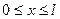 оси Ох. Мы будем считать, что концы струны
оси Ох. Мы будем считать, что концы струны 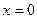 и
и 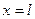 закреплены на оси Ох. Пусть струна растягивается силами
закреплены на оси Ох. Пусть струна растягивается силами 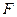 и
и 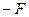 , приложенными к её концам в направлении вдоль оси Ох. Если струну вывести из состояния равновесия и затем предоставить себе самой, то под влиянием растягивающих сил точки струны придут в движение, стремясь вернуться в исходное положение. Однако, придя в это положение, каждая точка струны будет обладать уже некоторой скоростью и по инерции пройдёт дальше своего равновесного положения. При этом дальнейшем движении точек они будут тормозиться растягивающими силами и т.д. Таким образом, струна будет совершать некоторое колебательное движение. Задача состоит в исследовании этого движения.
, приложенными к её концам в направлении вдоль оси Ох. Если струну вывести из состояния равновесия и затем предоставить себе самой, то под влиянием растягивающих сил точки струны придут в движение, стремясь вернуться в исходное положение. Однако, придя в это положение, каждая точка струны будет обладать уже некоторой скоростью и по инерции пройдёт дальше своего равновесного положения. При этом дальнейшем движении точек они будут тормозиться растягивающими силами и т.д. Таким образом, струна будет совершать некоторое колебательное движение. Задача состоит в исследовании этого движения.
Сделаем ряд предположений. Прежде всего, мы считаем, что, выводя струну из состояния равновесия, мы придаём ей форму некоторой линии 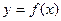 , лежащей на плоскости хОу и не сообщаем точкам струны никаких начальных скоростей. Тогда во всё время движения струна будет находиться в плоскости хОу. Мы будем предполагать, что каждая точка струны совершает только поперечные колебания, перпендикулярные оси Ох. Это колебание мы предположим столь малым, что квадратами отклонений точек струны от оси Ох можно пренебречь. Кроме того, будем считать, что во всё время движения струна будет сохранять пологую форму. Это означает, что угол
, лежащей на плоскости хОу и не сообщаем точкам струны никаких начальных скоростей. Тогда во всё время движения струна будет находиться в плоскости хОу. Мы будем предполагать, что каждая точка струны совершает только поперечные колебания, перпендикулярные оси Ох. Это колебание мы предположим столь малым, что квадратами отклонений точек струны от оси Ох можно пренебречь. Кроме того, будем считать, что во всё время движения струна будет сохранять пологую форму. Это означает, что угол 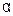 образуемый касательной к струне с осью Ох, достаточно мал, чтобы можно было считать
образуемый касательной к струне с осью Ох, достаточно мал, чтобы можно было считать
|
|
|
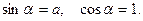 (1)
(1)
Наконец, мы считаем струну однородной, причём массу единицы длины струны в её нерастянутом состоянии обозначим 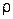 .
.
Возьмём какую - либо точку струны, имеющую в начальный момент 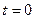 абсциссу
абсциссу 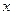 . Так как эта точка будет двигаться перпендикулярно оси Ох, то во время движения её абсцисса
. Так как эта точка будет двигаться перпендикулярно оси Ох, то во время движения её абсцисса 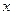 не будет меняться. Однако же её
не будет меняться. Однако же её 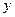 будет зависеть от времени, а также от того, о какой точке идёт речь, т.е. от абсциссы
будет зависеть от времени, а также от того, о какой точке идёт речь, т.е. от абсциссы 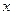 этой точки. Таким образом, эта ордината является функцией от
этой точки. Таким образом, эта ордината является функцией от 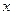 и от времени
и от времени 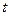 . Эту функцию мы будем обозначать через
. Эту функцию мы будем обозначать через 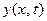 . Итак, дело сводится к нахождению функции
. Итак, дело сводится к нахождению функции 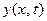 . Ясно, что эта неизвестная функция должна удовлетворять граничным условиям
. Ясно, что эта неизвестная функция должна удовлетворять граничным условиям
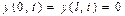 , (2)
, (2)
выражающим то, что концы струны 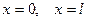 в любой момент времени находятся на оси Ох, и удовлетворяют начальным условиям
в любой момент времени находятся на оси Ох, и удовлетворяют начальным условиям
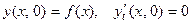 , (3)
, (3)
первое из которых выражает то, что в начальный момент 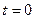 струне придана заданная форма
струне придана заданная форма 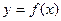 , а второе означает, что точки струны не имеют начальных скоростей.
, а второе означает, что точки струны не имеют начальных скоростей.
|
|
|
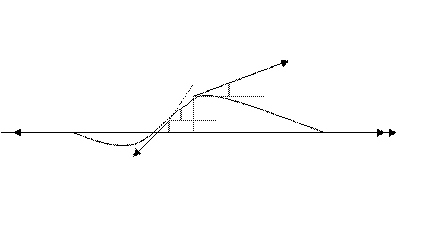
Выведем теперь дифференциальное уравнение, которому должна удовлетворять неизвестная функция 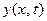 . Для этого выделим из струны элементарный отрезок, который в начальный момент
. Для этого выделим из струны элементарный отрезок, который в начальный момент 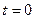 совпадает с отрезком
совпадает с отрезком 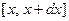 оси Ох. В момент
оси Ох. В момент 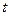 этот отрезок представляет собой элементарную дугу линии
этот отрезок представляет собой элементарную дугу линии 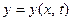 . Длина этой дуги равна
. Длина этой дуги равна
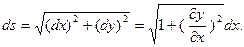
Пренебрегая членом 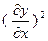 , (это основано в предпо- ложении пологой формы струныж однако,
, (это основано в предпо- ложении пологой формы струныж однако, 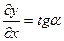 и значит,
и значит, 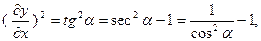 а мы считаем, что
а мы считаем, что 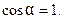 ) получим
) получим 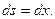
 Масса выделенного элемента равна
Масса выделенного элемента равна 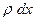 . К этому эле -менту будут приложены растягивающие его силы. Пусть натя- жение струны в точке
. К этому эле -менту будут приложены растягивающие его силы. Пусть натя- жение струны в точке  будет равно
будет равно 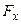 .
.
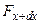
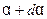
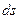
0 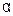
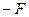

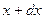
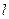
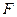 х
х
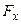
Рис. 13
Тогда к концам нашего элемента будут приложены силы 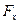 и
и 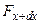 . Они направлены по касательным, проведённым к струне в точках
. Они направлены по касательным, проведённым к струне в точках  и
и 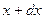 . Обозначим через
. Обозначим через 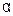 угол между осью Ох и касательной к струне в точке
угол между осью Ох и касательной к струне в точке  . В точке
. В точке 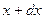 этот угол пусть будет равен
этот угол пусть будет равен 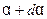 (Рис. 13).
(Рис. 13).
Обозначим равнодействующую сил, приложенных к концам элемента, через 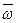 . Тогда векторное уравнение движения эле- мента имеет вид
. Тогда векторное уравнение движения эле- мента имеет вид
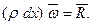 (4)
(4)
Проектируя это уравнение на ось Ох, находим
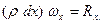 (5)
(5)
(Предостерегаем от недоразумений: символ 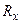 означает проекцию силы
означает проекцию силы 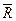 на ось Ох, а
на ось Ох, а 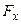 - численное значение натяжения в точке
- численное значение натяжения в точке  ).
).
Поскольку точки струны движутся перпендикулярно оси Ох, то 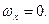 Стало быть и
Стало быть и 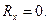 Но
Но
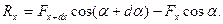
В силу (1), будет 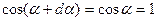 и потому
и потому 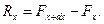 Сопоставляя это с равенством
Сопоставляя это с равенством 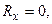 нахо -дим, что
нахо -дим, что 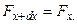 Это значит, что величина натяжения струны не меняется вдоль струны. Поскольку же на концах струны это натяжение равно
Это значит, что величина натяжения струны не меняется вдоль струны. Поскольку же на концах струны это натяжение равно 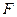 , то и во всех точках струны оно равно
, то и во всех точках струны оно равно 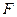 , и, вместо
, и, вместо 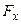 и
и 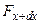 , можно писать
, можно писать 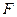 . Спроектируем теперь уравнение (4) на ось Оу
. Спроектируем теперь уравнение (4) на ось Оу
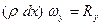 . (6)
. (6)
Так как 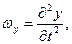 а (см. (1))
а (см. (1))
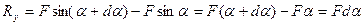 ,
,
то (6) даёт
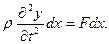 .
.
(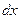 означает приращение угла
означает приращение угла 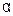 , когда в закреплённый мо- мент времени
, когда в закреплённый мо- мент времени 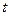 абсцисса
абсцисса  получает приращение
получает приращение 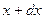 . Поэтому отношение
. Поэтому отношение 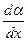 есть, строго говоря, частная произ- водная
есть, строго говоря, частная произ- водная 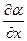 ). Или
). Или
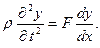 (7)
(7)
Вспомним теперь, что 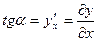 . Отсюда
. Отсюда
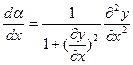 .
.
Как и выше, членом 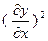 можно пренебречь, откуда
можно пренебречь, откуда
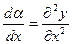 .
.
Положив для краткости 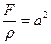 , приводим уравнение (7) к виду
, приводим уравнение (7) к виду
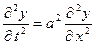 . (8)
. (8)
Это знаменитое уравнение колебания струны. Мы видим, что это дифференциальное уравнение с частными произ -водными. Такие уравнения до сих пор мы ещё не изучали.
Таким образом, наша механическая задача свелась к чисто математической: найти такое решение уравнения (8), которое удовлетворяет условиям (2) и (3).
Существуют разные способы решить задачу, к которой мы пришли.
Один из способов был предложен в 18 веке Д. Бернулли. Позже, уже в 19 веке, этот способ систематически применялся Фурье для решения целого ряда термодинамических задач, почему он и получил название метода Фурье. Этот способ мы и изложим. Он заключается в том, что сначала решается следующая задача.
Вспомогательная задача: Найти функцию 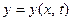 , удовлетворяющую требованиям:
, удовлетворяющую требованиям:
1) 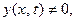 тождественно, (9)
тождественно, (9)
2) 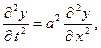 (10)
(10)
3) 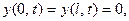 (11)
(11)
4) 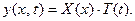 (12)
(12)
Отличие вспомогательной задачи от той, которую нам на самом деле нужно решить, состоит в том, что от искомой функции 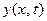 мы уже не требуем, чтобы она удо- влетворяла начальным условиям (3), но зато требуем, чтобы она имела специальный вид
мы уже не требуем, чтобы она удо- влетворяла начальным условиям (3), но зато требуем, чтобы она имела специальный вид 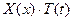 , т.е. представлялась в виде произведения функции
, т.е. представлялась в виде произведения функции 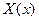 от одного только
от одного только  на функцию
на функцию 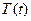 одного только
одного только 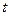 . Кроме того, мы налагаем на функцию
. Кроме того, мы налагаем на функцию 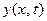 естественное условие, а именно она не должна быть тождественным нулём.
естественное условие, а именно она не должна быть тождественным нулём.
Оказывается, что изменённая таким образом задача, решается довольно легко и что она имеет бесконечное множество решений, из которых удаётся составить и решение нашей основной задачи.
Займёмся же поставленной вспомогательной задачей.
Из (9) вытекает существование такой точки 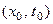 , что
, что 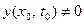 . Тогда
. Тогда 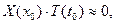 т.е.
т.е. 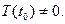 Подста -вим значение
Подста -вим значение 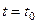 в граничные условия (11):
в граничные условия (11):
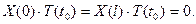
Отсюда видно, что искомая функция 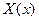 должна удовле- творять условиям:
должна удовле- творять условиям:
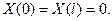 (13)
(13)
Подставляя (12) в (10) получим
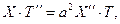
т.е.
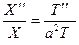 . (14)
. (14)
Но (внимание!) правая часть равенства (14) не зависит от  . Значит и левая часть (14) от
. Значит и левая часть (14) от  не должна зависеть. С другой стороны, эта левая часть может быть функцией только одного
не должна зависеть. С другой стороны, эта левая часть может быть функцией только одного  , так как
, так как 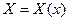 . Значит, левая (а с ней и пра- вая) часть равенства должна быть постоянной величиной. Обозначим эту (неизвестную нам) постоянную через
. Значит, левая (а с ней и пра- вая) часть равенства должна быть постоянной величиной. Обозначим эту (неизвестную нам) постоянную через 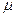 .
.
|
|
|
Допустим сначала, что 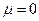 . Тогда из (14) следует,
. Тогда из (14) следует,
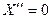 .
.
Отсюда 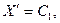 и
и 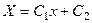 , т.е.,
, т.е.,  должна быть линейной функцией. Подставляя найденное значение
должна быть линейной функцией. Подставляя найденное значение  в условие (13), получим
в условие (13), получим 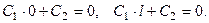 Но тогда
Но тогда 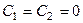 , т.е.
, т.е. 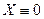 , а с ним и
, а с ним и 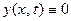 , что проти- воречит (9). Таким образом, не существует решения вспомо -гательной задачи, у которой было бы
, что проти- воречит (9). Таким образом, не существует решения вспомо -гательной задачи, у которой было бы 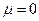 .
.
Допустим теперь, что 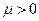 , т.е. что
, т.е. что 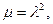 где
где 
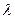 мож -но считать положительным. Тогда
мож -но считать положительным. Тогда
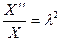 , т.е.
, т.е. 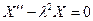 .
.
Общее решение этого линейного уравнения имеет вид
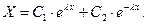
Подставляя найденное значение 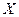 в (13), получим
в (13), получим
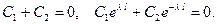
Решая эту систему, находим 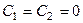 . Это снова приводит к соотношению
. Это снова приводит к соотношению 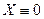 , противоречащему условию (9). Итак, неравенство
, противоречащему условию (9). Итак, неравенство 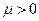 тоже оказывается невозможным. Стало быть, вспомогательную задачу можно рассматривать, только предполагая, что неизвестное
тоже оказывается невозможным. Стало быть, вспомогательную задачу можно рассматривать, только предполагая, что неизвестное 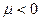 , т.е., что
, т.е., что 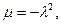 где
где 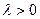 . Таким образом,
. Таким образом,
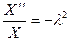 или
или 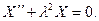
Решение этого уравнения есть
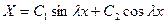
Первое из граничных условий (13) даёт 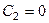 . Значит (заменяя
. Значит (заменяя 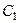 , на
, на 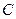 ),
),
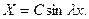
Если бы было  , то мы не пришли бы к решению нашей вспомогательной задачи, ибо получилось бы проти- воречие с (9). Стало быть
, то мы не пришли бы к решению нашей вспомогательной задачи, ибо получилось бы проти- воречие с (9). Стало быть 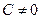 . Но тогда второе из условий (13) даёт
. Но тогда второе из условий (13) даёт 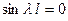 . Это возможно лишь при
. Это возможно лишь при
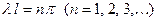 .
.
Значит для 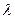 возможны лишь значения
возможны лишь значения
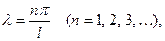
что приводит к следующим выражениям для 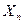 :
:
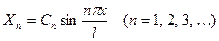 ,
,
причём 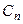 при каждом
при каждом 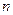 может принять любое (отличное от 0) значение.
может принять любое (отличное от 0) значение.
Выберем какое-либо из возможных значений 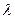 и подста -вим в (14):
и подста -вим в (14):
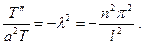
Отсюда
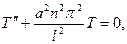
т.е.
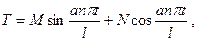
где 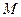 и
и 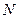 - произвольные постоянные. Обозначая Это
- произвольные постоянные. Обозначая Это 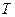 через
через 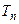 и полагая
и полагая 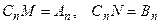 получаем бесконечное множество решений вспомогательной задачи
получаем бесконечное множество решений вспомогательной задачи
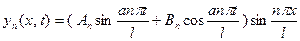 . (15)
. (15)
Здесь 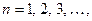 а
а 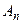 и
и 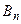 - произвольные постоянные.
- произвольные постоянные.
Любая функция (15) удовлетворяет уравнению (10) и граничным условиям (11), причём это верно уже и без ограничений 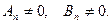
Заметим теперь, что и уравнение (10) и условия (11) линейны и однородны, т.е. таковы, что сумма функций, удовлетворяющих им, также будет удовлетворять и уравнению и граничным условиям. Поэтому функция
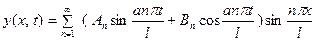 (16)
(16)
при условии сходимости выписанного ряда, также будет удо-влетворять уравнению (10) и граничным условиям (11). Отме- тим, что 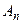 и
и 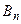 остаются при этом произвольными посто- янными (при условии, что не нарушается сходимость получен- ного ряда). Чтобы функция (16) была решением интересующей нас (уже не вспомогательной, а основной) задачи, нужно подо- брать
остаются при этом произвольными посто- янными (при условии, что не нарушается сходимость получен- ного ряда). Чтобы функция (16) была решением интересующей нас (уже не вспомогательной, а основной) задачи, нужно подо- брать 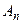 и
и 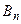 так, чтобы выполнялись начальные условия (3).
так, чтобы выполнялись начальные условия (3).
|
|
|
Первое условие (3) даёт
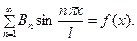 (17)
(17)
Дифференцируя (16), получим
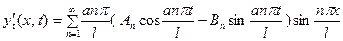 .
.
Полагая 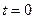 и учитывая второе из условий (3), получим
и учитывая второе из условий (3), получим
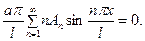 (18)
(18)
Чтобы удовлетворить соотношение (18) нужно принять, 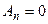 (
(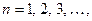 ) Соотношение же (17) показывает, что коэффициенты
) Соотношение же (17) показывает, что коэффициенты 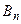 должны быть коэффициентами разложения функции
должны быть коэффициентами разложения функции 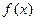 , заданной на
, заданной на 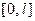 по функциям
по функциям 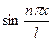 , т.е
, т.е
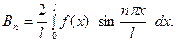 (19)
(19)
Сдедовательно, искомое решение имеет вид
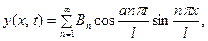
где 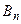 определяется из (19).
определяется из (19).
ПРИМЕР. Пусть 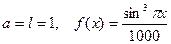 . Найти
. Найти 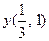 .
.
Решение. Найдём сначала разложение (17). Это гораздо проще сделать без использования формул (19), непосредст- венно. Действительно,
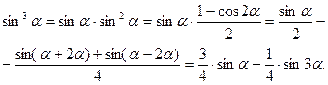
Значит, 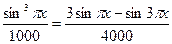 ,
,
откуда 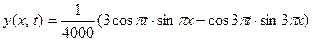
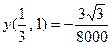 .
.
2 Распространение тепла в стержне.
В качестве другого применения рядов Фурье рассмотрим задачу о распространении тепла в стержне. Пусть стержень длины 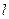 весь, кроме своих концов, помещён в теплоизо -лирующую оболочку и нагрет до некоторой температуры, различной в различных его точках. Если этот стержень пре- доставить самому себе, то заключённое в нём тепло будет перетекать от более нагретых точек к менее нагретым, и температура стержня с течением времени станет вырав- ниваться, причём на этот процесс будет влиять также и режим, который поддерживается на концах стержня. Задача состоит в том, чтобы, зная упомянутый режим, и распреде- ление температур вдоль стержня в начальный момент
весь, кроме своих концов, помещён в теплоизо -лирующую оболочку и нагрет до некоторой температуры, различной в различных его точках. Если этот стержень пре- доставить самому себе, то заключённое в нём тепло будет перетекать от более нагретых точек к менее нагретым, и температура стержня с течением времени станет вырав- ниваться, причём на этот процесс будет влиять также и режим, который поддерживается на концах стержня. Задача состоит в том, чтобы, зная упомянутый режим, и распреде- ление температур вдоль стержня в начальный момент 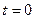 , найти это распределение в последующие моменты
, найти это распределение в последующие моменты 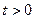 . Для этого естественно надо задать и термические характеристики стержня:: его теплоёмкость
. Для этого естественно надо задать и термические характеристики стержня:: его теплоёмкость 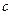 и коэффициент теплопровод- ности
и коэффициент теплопровод- ности 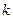 . Напомним, что
. Напомним, что 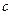 - это количество калорий, которое нужно подать, чтобы единицу массы стержня (мы считаем его однородным с линейной плотностью
- это количество калорий, которое нужно подать, чтобы единицу массы стержня (мы считаем его однородным с линейной плотностью 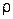 нагреть на
нагреть на 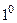 . Коэф- фициент
. Коэф- фициент 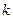 представляет собой количество тепла (в калори -ях), которое будет протекать за единицу времени через сечение стержня, если температура стержня падает на
представляет собой количество тепла (в калори -ях), которое будет протекать за единицу времени через сечение стержня, если температура стержня падает на 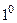 при перемещении вдоль стержня на единицу длины. Мы будем обозначать температуру стержня в точке
при перемещении вдоль стержня на единицу длины. Мы будем обозначать температуру стержня в точке  (один из концов стержня (назовём его «левым») фиксируется и точкой
(один из концов стержня (назовём его «левым») фиксируется и точкой  называется точка, отстоящая от этого конца на расстояние
называется точка, отстоящая от этого конца на расстояние  ) в момент времени
) в момент времени 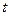 через
через 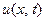 . Это и есть та вели- чина, которую нужно найти. Температуру же
. Это и есть та вели- чина, которую нужно найти. Температуру же 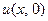 стержня в начальный момент мы считаем известной и обозначаем через
стержня в начальный момент мы считаем известной и обозначаем через 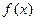
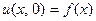 . (20)
. (20)
Что касается температурного режима на концах стержня, этот режим может быть весьма разнообразен. Можно, напри -мер, на концах отрезка поддерживать температуру, изменяю- щуюся по заданным законам 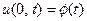 ,
, 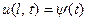 и т.п.), то мы рассмотрим два случая:
и т.п.), то мы рассмотрим два случая:
А) концы погружены в тающий лёд, т.е. в них поддержи- вается постоянная температура
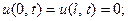 (21)
(21)
В) концы погружены в ту же теплоизолирующую оболочку, что и весь стержень. Это означает, что через концы не про -исходит протекание тепла. Математическое выражение этой за- кономерности мы найдём несколько позже.
Рассмотрим сечение  нашего стержня и найдём какое ко- личество
нашего стержня и найдём какое ко- личество 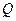 тепла протечёт (слева направо) через это сече- ние за элементарный промежуток времени
тепла протечёт (слева направо) через это сече- ние за элементарный промежуток времени 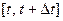 . В мо -мент
. В мо -мент 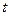 температура стержня в точке
температура стержня в точке  будет равна
будет равна 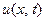 .
.
Возьмём отличную от  точку
точку 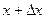 стержня. Пусть, для определённости,
стержня. Пусть, для определённости, 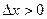 , т.е. новая точка лежит правее ста -рой. В ней температура стержня в момент
, т.е. новая точка лежит правее ста -рой. В ней температура стержня в момент 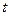 будет равна
будет равна 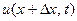 . Таким образом, падение температуры при пере- мещении из
. Таким образом, падение температуры при пере- мещении из  в
в 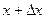 оказывается равным
оказывается равным
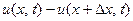 .
.
Следлвательно, на единицу длины стержня (на участке 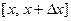 ) приходится падение температуры, равное
) приходится падение температуры, равное
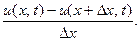
Если 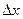 весьма мало, то найденную величину можно при -нять за
весьма мало, то найденную величину можно при -нять за 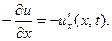 Такое падение температуры застави- ло бы за единицу времени перейти сечение
Такое падение температуры застави- ло бы за единицу времени перейти сечение  количество тепла, равное
количество тепла, равное 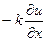 калорий. За время же
калорий. За время же 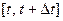 через наше сечение перейдёт (слева направо)
через наше сечение перейдёт (слева направо)
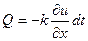 (22)
(22)
калорий.. (Если 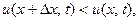 то температура падает при перемещении слева направо. В этом случае тепло поте -чёт через сечение
то температура падает при перемещении слева направо. В этом случае тепло поте -чёт через сечение  также слева направо, т.е. окажется
также слева направо, т.е. окажется 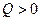 . Это вполне согласуется с тем, что в нашем случае
. Это вполне согласуется с тем, что в нашем случае 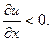 Если же
Если же 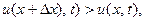 то тепло потечёт справа налево, т.е. будет
то тепло потечёт справа налево, т.е. будет 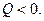 Но тогда
Но тогда 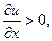 и форму- ла (22) снова будет справедливой.)
и форму- ла (22) снова будет справедливой.)
Если концы стержня теплоизолированы, то количество тепла, протекающее через них, равно 0, и потому
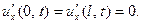 (23)
(23)
Это и есть то выражение режима 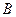 , о котором мы упомя -нули выше.
, о котором мы упомя -нули выше.
Выделим из нашего стержня элементарный отрезок 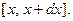 За время
За время 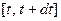 через сечение
через сечение  в наш отре- зок войдёт (из расположенной левее
в наш отре- зок войдёт (из расположенной левее  части стержня)
части стержня)
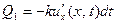
калорий. За это же время из нашего отрезка через его конец 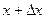 уйдёт направо
уйдёт направо
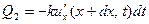
калорий. Стало быть, в рассматриваемом отрезке за время 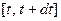 накопится количество тепла, равное
накопится количество тепла, равное
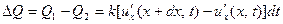
калорий. Поскольку малое приращение функции можно заме -ить её дифференциалом, то
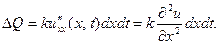
Подача такого количества тепла должна повысить темпе -ратуру единицы массы стержня на
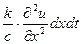
градусов. Поскольку же масса отрезка 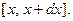 равна
равна 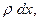 то соответствующее повышение температуры будет
то соответствующее повышение температуры будет
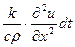 . (24)
. (24)
С другой стороны, это повышение температуры 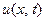 в точке
в точке  за время
за время 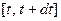 равно
равно
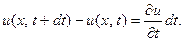 (25)
(25)
Приравнивая друг к другу выражения (23) и (24), и, полагая для краткости, 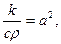 получим уравнение теплопровод- ности
получим уравнение теплопровод- ности
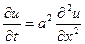 . (26)
. (26)
Таким образом, мы приходим к двум математическим задачам:
А) Найти то решение уравнения (26), которое удовлетво -ряет начальному условию (20) и граничным условиям (21).
В) То же с заменой условий (21) на (23).
Применим к задаче А) метод Фурье. Для этого сначала ре- шим вспомогательную задачу: найти функцию 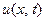 не рав- ную нулю тождественно, удовлетворяющую уравнению (26) и граничным условиям (21) и имеющую специальный вид
не рав- ную нулю тождественно, удовлетворяющую уравнению (26) и граничным условиям (21) и имеющую специальный вид
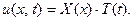 (27)
(27)
Как и при решении уравнения колебания струны, легко по- казать, что из (21) следует
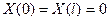 . (28)
. (28)
Подставляя (26) в (27), получим
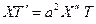 ,
,
т.е.
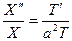 . (29)
. (29)
Соотношение (29) возможно лишь тогда, когда обе его части представляют одну и ту же постоянную. Обозначим её через 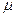 . На основании (28), допущения
. На основании (28), допущения 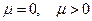 невоз-
невоз-
можны. Следовательно, 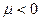 . Полагая
. Полагая 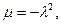 и, букваль -но повторяя рассуждения из 1, по формуле (29) получаем, что
и, букваль -но повторяя рассуждения из 1, по формуле (29) получаем, что
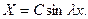
Более того, как и в 1, устанавливаем, что 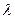 может иметь только одно из значений
может иметь только одно из значений 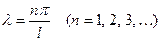 . Следова -тельно,
. Следова -тельно, 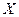 может иметь любое из выражений
может иметь любое из выражений
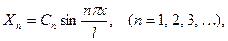
где 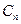 - произвольные постоянные. Выбирая какое – либо из возможных значений
- произвольные постоянные. Выбирая какое – либо из возможных значений 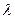 и приравнивая правую часть равенс- тва (29) величине
и приравнивая правую часть равенс- тва (29) величине 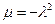 , находим
, находим
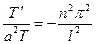 ,
,
т.е.
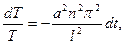
откуда,
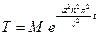 ,
,
где 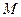 - произвольная постоянная. Полагая
- произвольная постоянная. Полагая 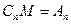 , находим бесконечное множество решений вспомогательной за -дачи
, находим бесконечное множество решений вспомогательной за -дачи
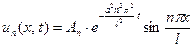 . (30)
. (30)
Каждая из этих функций при любых 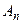 удовлетворяет уравнению (26) и граничным условиям (21). Ввиду линейности уравнения и граничных условий, сумма
удовлетворяет уравнению (26) и граничным условиям (21). Ввиду линейности уравнения и граничных условий, сумма
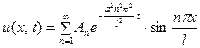 (31)
(31)
при любом выборе 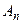 , сохраняющем сходимость написанного ряда, также будет решением (26), удовлетворяющим (21). По- стараемся же подобрать
, сохраняющем сходимость написанного ряда, также будет решением (26), удовлетворяющим (21). По- стараемся же подобрать 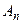 так, чтобы удовлетворить и на -чальному условию
так, чтобы удовлетворить и на -чальному условию 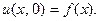 Ясно, что это приводит к равенству
Ясно, что это приводит к равенству
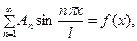
откуда
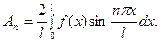 (32)
(32)
Итак задача А) решена. Её решение даётся формулой (31), в которой 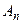 нужно вычислять по (32).
нужно вычислять по (32).
Полезно заметить, что из (31) следует, что
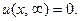
Физический смысл этого соотношения ясен: всё тепло из стержня вытечет и в нём установится температура льда, в который погружены его концы.
Перейдём к задаче В). Для неё вспомогательная задача состоит в нахождении функции 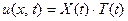 не равной нулю тождественно, удовлетворяющей уравнению (26) и усло- виям (23) Последние дают:
не равной нулю тождественно, удовлетворяющей уравнению (26) и усло- виям (23) Последние дают:
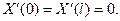 (33)
(33)
Подстановка 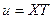 в (26) снова приводит к уравнению
в (26) снова приводит к уравнению
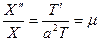 , (34)
, (34)
где 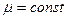 . Случай
. Случай 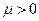 исключается, как и выше. Но соотношение
исключается, как и выше. Но соотношение 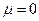 уже возможно. Оно даёт:
уже возможно. Оно даёт: 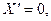 откуда
откуда
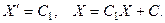 Согласно (33), будет
Согласно (33), будет 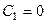 и потому
и потому  , где
, где 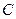 - произвольная постоянная. Кроме того, при
- произвольная постоянная. Кроме того, при 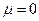 уравнение (34) даёт
уравнение (34) даёт 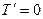 , т.е. и
, т.е. и 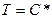 , где
, где 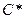 - постоянная. Следовательно, одним из решений вспомога -тельной задачи будет
- постоянная. Следовательно, одним из решений вспомога -тельной задачи будет
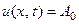 .
.
При любом выборе 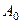 (хотя бы и
(хотя бы и 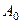 = 0) эта функция удо -влетворяет соотношениям (26) и (23).
= 0) эта функция удо -влетворяет соотношениям (26) и (23).
Предположим теперь, что 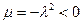 . Это даёт уравнение
. Это даёт уравнение
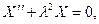
решение которого имеет вид:
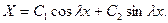
Но тогда
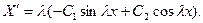
и первое из соотношений (33) даёт 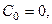 так что (после замены
так что (после замены 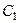 на
на 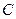 ) принимает вид
) принимает вид
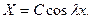
Отсюда и из второго условия (69) получим
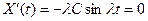 .
.
Значит, 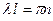
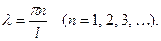 (35)
(35)
Таким образом, найдено бесконечное множество выражений функции 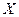 :
:
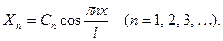
Подставив в (34) одно из значений (35), получим
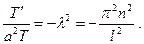
Отсюда
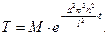
Положив 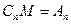 , находим бесконечное множество функций
, находим бесконечное множество функций
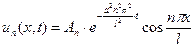 ,
,
удовлетворяющих (26) и (23). Но тогда и
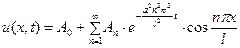 (36)
(36)
будет решением (26), удовлетворяющим (23). Остаётся подо -брать 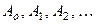 так, чтобы оказалось
так, чтобы оказалось 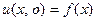 , т.е.
, т.е.
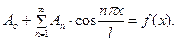
Для этого необходимо взять
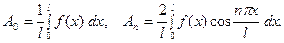 (37)
(37)
Замечание. Из (36) видим, что
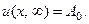
Этим выражен физически очевидный факт, что с течением времени температура в изолированном стержне вырав- нивается. Более того, ясно и значение этой выровненной температуры. Именно, найдём общее количество тепла, содержащегося в нашем стержне. Для этого выделим из него элемент 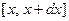 . В начальный момент температура этого элемента равна
. В начальный момент температура этого элемента равна 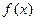 . Поскольку масса элемента равна
. Поскольку масса элемента равна 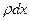 , то для получения указанной температуры нужно было накопить в элементе
, то для получения указанной температуры нужно было накопить в элементе 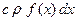 калорий.
калорий.
Стало быть, общее количество тепла в стержне будет равно
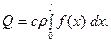
Поскольку стержень изолирован, то это же количество тепла сохранится в нём и при 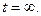 На единицу массы стержня придётся
На единицу массы стержня придётся
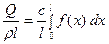
калорий. Это количество тепла и создаёт в стержне температуру
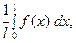
найденную выше.
§ 7 ПРЕОБРАЗОВАНИЕ ФУРЬЕ.
Одним из мощных средств исследования задач математической физики является метод интегральных преобразований.
Пусть функция 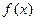 задана на интервале
задана на интервале 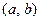 , конечном или бесконечном. Интегральным преобразованием функции
, конечном или бесконечном. Интегральным преобразованием функции 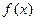 называется функция
называется функция
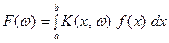 ,
, 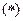
где 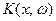 фиксированная для данного преобразования функция, называемая ядром преобразования (предполагается, что интеграл (*) существует в собственном или несобственном смысле).
фиксированная для данного преобразования функция, называемая ядром преобразования (предполагается, что интеграл (*) существует в собственном или несобственном смысле).
 2015-01-30
2015-01-30 2637
2637








