Целесообразно применять, когда общий член ряда порождает функцию, первообразная которой находится без особого труда.
Если 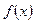 - непрерывная, положительная, убывающая в
- непрерывная, положительная, убывающая в 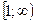 , значения которой при натуральных значениях аргумента
, значения которой при натуральных значениях аргумента 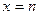 совпадают с соответствующими значениями ряда
совпадают с соответствующими значениями ряда
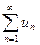 , то этот ряд и несобственный интеграл
, то этот ряд и несобственный интеграл 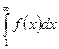 одновременно сходятся или расходятся.
одновременно сходятся или расходятся.
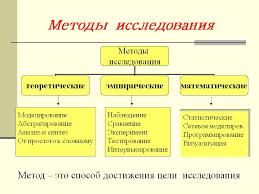
Исследование знакопостоянных рядов:
- проверить необходимое условие;
- применить признак Даламбера, радикальный признак Коши, интегральный признак Коши или признаки сравнения.
3.3. Знакопеременные ряды:
Теорема (общий достаточный признак):
Если сходится ряд, составленный из абсолютных величин членов знакопеременного ряда, то сходится и знакопеременный ряд.
Определение: знакопеременный ряд, положительные и отрицательные члены которого следуют друг за другом строго поочередно, называется знакочередующимся.
Теорема (признак Лейбница):
Если абсолютные величины членов знакочередующегося ряда убывая стремятся к нулю, то такой ряд сходится и абсолютная величина его суммы не превосходит абсолютной величины первого члена ряда.
Ряд, отвечающий условиям признака Лейбница, называется лейбницевским. Любой лейбницевский ряд сходится.
Исследование сходимости знакопеременных рядов:
- проверить необходимое условие;
- проверить для ряда условия Лейбница;
- составить ряд из абсолютных величин (если он сходится, то данный ряд сходится абсолютно; если он расходится, то данный ряд сходися условно)
3.4. Степенные ряды:
Определение:
Ряд, все члены которого являются функциями одного и тогоже аргумента называется функциональным.
Его общий вид: 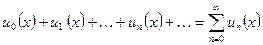 .
.
Определение:
Функциональный ряд вида 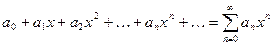 , где коэффициенты ряда
, где коэффициенты ряда 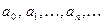 - любые действительные числа, называется степенным, расположенным по степеням
- любые действительные числа, называется степенным, расположенным по степеням 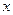 .
.
Исследование сходимости степенных рядов:
-находим радиус сходимости 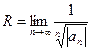 или
или 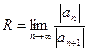 , записываем интервал сходимости;
, записываем интервал сходимости;
- проверяем поведение ряда на концах интервала;
- находим область сходимости.
3.5. Ряд Тейлора:
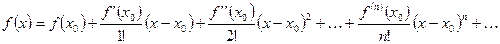
Ряд, стоящий в правой части равентсва называется рядом Тейлора по функции 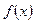 .
.
При 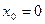 ряд Тейлора принимает вид:
ряд Тейлора принимает вид:
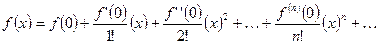
 и называется рядом Маклорена.
и называется рядом Маклорена.
3.6. Разложение элементарных функций в ряд по степеням 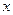 :
:
1. 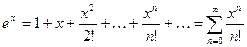 ;
; 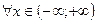
2. 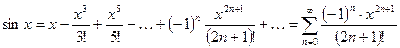 ;
; 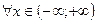
3. 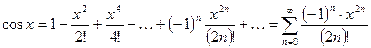 ;
; 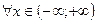
4. 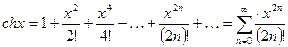 ;
; 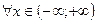
5. 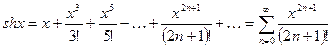 ;
; 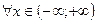
6. 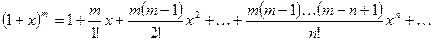 ;
; 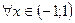
7. 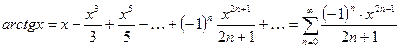 ;
; 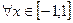
8. 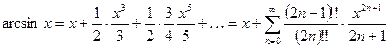 ;
; 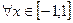
9. 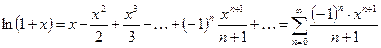 ;
; 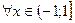
10. 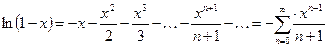 ;
; 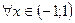
11. 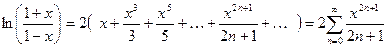 ;
; 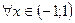
3.7. Ряды Фурье. Теорема Дирихле.
Определение:
Функция 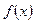 , называется удовлетворяющей условиям Дирихле на
, называется удовлетворяющей условиям Дирихле на 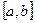 , если она на этом отрезке
, если она на этом отрезке
· непрерывна или имеет конечное число точек разрыва первого рода;
· имеет конечное число строгих экстремумов.
·
Теорема Дирихле (достаточное условие разложимости функции в ряд Фурье):
Если функция 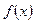 отвечает на отрезке
отвечает на отрезке 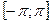 условиям Дирихле, то ее ряд Фурье сходится в каждой точке этого отрезка, причем во внутренних точках непрерывности функции
условиям Дирихле, то ее ряд Фурье сходится в каждой точке этого отрезка, причем во внутренних точках непрерывности функции 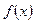 ряд сходится к самой функции
ряд сходится к самой функции 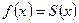 . В каждой внутренней точке разрыва
. В каждой внутренней точке разрыва 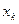 функции
функции 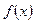 ряд сходится к среднему арифметическому предельных значений этой функции в точке
ряд сходится к среднему арифметическому предельных значений этой функции в точке 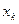 слева и справа, т.е.
слева и справа, т.е. 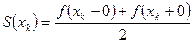 . В обеих граничных точках
. В обеих граничных точках 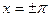 ряд сходится к среднему арифметическому предельных значений функции в этих точках, когда
ряд сходится к среднему арифметическому предельных значений функции в этих точках, когда 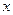 стремится к ним изнутри отрезка, т.е.
стремится к ним изнутри отрезка, т.е. 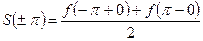 .
.
Алгоритм разложения периодических функции в ряд Фурье на 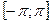 :
:
- строим график на 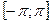 и с его помощью проверяем выполнение условий Дирихле;
и с его помощью проверяем выполнение условий Дирихле;
- устанавливаем ожидаемую форму ряда Фурье;
- вычисляем коэффициенты по формулам Эйлера-Фурье и составляем формальный ряд;
- строим на заданном отрезке график суммы 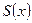 ряда;
ряда;
- периодически продолжаем грифики функции и суммы на всю числовую ось;
- определяем точки сходимости ряда к самой функции 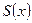 ;
;
Аналогично, раскладываются в ряд Фурье периодические функции на 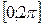 ;
; 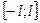 ;
; 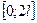 .
.
Алгоритм разложения в ряд Фурье нерериодических функций, заданных на 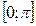 ;
; 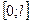 по косинусам (по синусам):
по косинусам (по синусам):
- продолжаем функцию 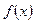 четным (нечетным) образом на
четным (нечетным) образом на 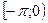 (
(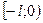 ) и получаем новую функцию
) и получаем новую функцию  ;
;
- строим график  и проверяем условия Дирихле;
и проверяем условия Дирихле;
- устанавливаем ожидаемую форму ряда Фурье;
- вычисляем коэффициенты по формулам Эйлера-Фурье и составляем формальный ряд 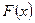 ;
;
- строим на заданном отрезке график суммы 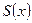 ряда;
ряда;
- определяем точки сходимости ряда к самой функции 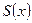 ;
;
Если 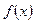 - общего положения на
- общего положения на 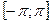 , то ее можно разложить в ряд Фурье вида:
, то ее можно разложить в ряд Фурье вида:
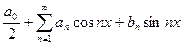 , где
, где 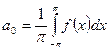 ;
;
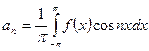 , где
, где 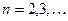
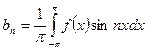 , где
, где 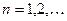
Если 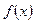 - общего положения на
- общего положения на 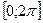 , то ее можно разложить в ряд Фурье вида:
, то ее можно разложить в ряд Фурье вида:
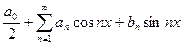 , где
, где 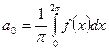 ;
;
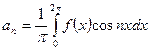 , где
, где 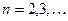
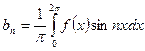 , где
, где 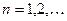
Если 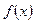 - общего положения на
- общего положения на 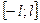 , то ее можно разложить в ряд Фурье вида:
, то ее можно разложить в ряд Фурье вида:
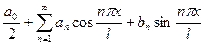 , где
, где 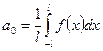 ;
;
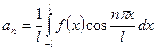 , где
, где 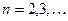
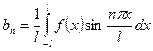 , где
, где 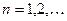
Если 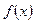 - четная на
- четная на 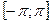 , то ее можно разложить в ряд Фурье вида:
, то ее можно разложить в ряд Фурье вида:
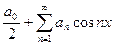 , где
, где 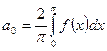 ;
;
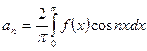 , где
, где 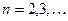
Если 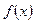 - нечетная на
- нечетная на 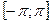 , то ее можно разложить в ряд Фурье вида:
, то ее можно разложить в ряд Фурье вида:
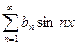 , где
, где 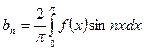 , где
, где 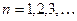
При вычислении интегралов, учитываем, что 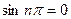 и
и 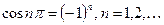
РАЗДЕЛ IV: ТЕОРИЯ ФУНКЦИЙ КОМПЛЕКСНОГО ПЕРЕМЕННОГО.
4.1. Основные понятия:
Определение: соответствие 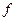 , при котором каждому значению
, при котором каждому значению 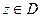 отвечает одно или несколько значений
отвечает одно или несколько значений 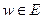 называется функцией комплексной переменной
называется функцией комплексной переменной 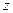 .
.
Обозначение: 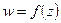 .
.
Функция комплексного переменного может быть одноизначной и многозначной.
Т.к. 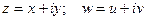 , то
, то 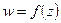 можно представить как
можно представить как 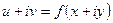 .
.
Здесь 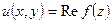 , а
, а 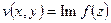 .
.
Определение (для однозначных или отдельных вертвей многозначных):
Комплексное число 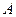 называется пределом функции
называется пределом функции 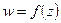 при
при 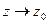 , если для
, если для 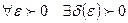 такое, что при всех
такое, что при всех 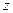 отличных от
отличных от 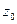 и удовлетворяющих неравенству
и удовлетворяющих неравенству 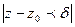 справедливо неравенство
справедливо неравенство 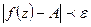 .
.
Обозначение: 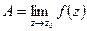 .
.
Если 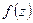 представлена в виде
представлена в виде 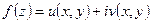 , то она непрерывна в точке
, то она непрерывна в точке 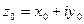 тогда и только тогда, когда в точке
тогда и только тогда, когда в точке 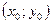 одновременно непрерывны ее действительная часть
одновременно непрерывны ее действительная часть 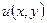 и мнимая
и мнимая 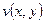 .
.
Определение:
Функция 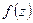 непрерывная в каждой точке некоторого множества называется непрерывной на этом множестве.
непрерывная в каждой точке некоторого множества называется непрерывной на этом множестве.
Определение (для однозначных или отдельных вертвей многозначных): 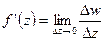 ;
;
Дифференциал фкп находят по формуле: 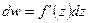 .
.
Если 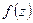 дифференцируема в точке
дифференцируема в точке 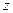 , то она в этой точке и непрерывна, обратное не справедливо.
, то она в этой точке и непрерывна, обратное не справедливо.
Функция 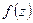 называется дифференцируемой на некотором множестве, если она дифференцируема в каждой точке этого множества.
называется дифференцируемой на некотором множестве, если она дифференцируема в каждой точке этого множества.
Теорема (необходимое и достаточное условия дифференцируемости фкп):
Для того чтобы однозначная функция 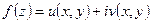 была дифференцируемой в точеке
была дифференцируемой в точеке 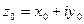 необходимо и достататочно, чтобы в т.
необходимо и достататочно, чтобы в т. 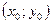 :
:
- 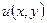 и
и 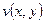 были дифференцируемы;
были дифференцируемы;
- выполнялись равенства 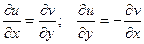 (условия Даламбера - Эйлера или Римана - Коши).
(условия Даламбера - Эйлера или Римана - Коши).
Определение:
Функция 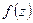 называется аналитической в точке, если она однозначна и дифференцируема в этой точке и ее окрестности.
называется аналитической в точке, если она однозначна и дифференцируема в этой точке и ее окрестности.
Определение:
Функция 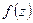 называется аналитической в области, если она аналитическая в каждой точке этой области.
называется аналитической в области, если она аналитическая в каждой точке этой области.
Примечание: функции, содержащие 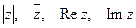 не являются аналитическими.
не являются аналитическими.
4.2. Основные элементарные функции:
1. Степенная функция 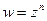
а) если 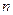 - натуральное, то
- натуральное, то 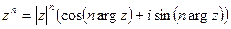 и
и 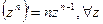 ;
;
б) если 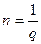 , где
, где 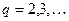 ,то
,то 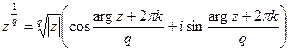 ,
, 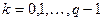
в) если 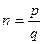 , где
, где 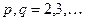 и
и 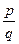 - несократимая, то
- несократимая, то
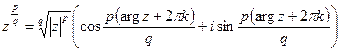 ,
, 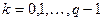 .
.
2. Показательная функция 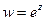
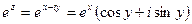
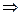
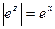 и
и 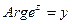 , (
, (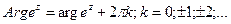 и
и 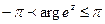 )
)
Специфическое свойство: 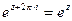 , при
, при 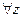
3. Логарифмическая функция 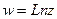
Формула вычисления - 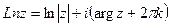 , где
, где 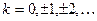
Если 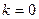 , то имеем главную ветвь -
, то имеем главную ветвь - 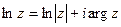 , т.е.
, т.е. 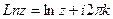 , где
, где
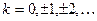
4. Тригонометрические функции
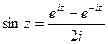 ;
; 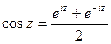 ;
; 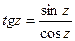 ;
; 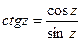 .
.
Специфическое свойство: 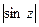 и
и 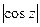 могут быть большими единицы.
могут быть большими единицы.
5. Гиперболические функции
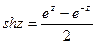 ;
; 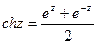 ;
; 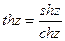 ;
; 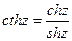
Формулы связи: 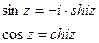 и
и 
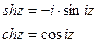 .
.
Функции 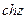 и
и 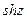 - периодические с периодом
- периодические с периодом 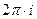 , а
, а 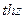 и
и 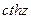 -
- 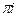 .
.
Характерно, что 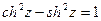 и
и 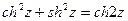 .
.
6. Обобщенные степенная и показательные функции (не относятся к числу основных элементарных, но являются элементарными)
- обобщенная степенная функция 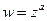 , где
, где 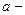 любое комплексное число, функция определяется равенством
любое комплексное число, функция определяется равенством 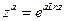 ;
;
- обобщенная показательная функция 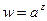 , где а – любое комплексное число
, где а – любое комплексное число 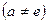 , функция определяется равенством
, функция определяется равенством 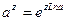
4.3. Определение и свойства контурного интеграла по кривой:
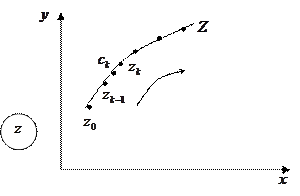
Пусть в плоскости Гаусса задана гладкая направленная кривая 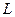 с начальной точкой
с начальной точкой 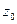 и конечной
и конечной 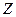 и пусть в каждой точке этой кривой определена однозначная непрерывная функция
и пусть в каждой точке этой кривой определена однозначная непрерывная функция 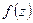 .
.
Определение: Конечный предел интегральной суммы функции 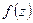 на кривой
на кривой 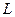 при условии, что
при условии, что 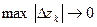 и
и 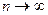 называется контурным интегралом от этой функции по кривой
называется контурным интегралом от этой функции по кривой 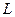 , где
, где 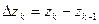
Т.о. 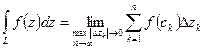 .
.
Основные свойства:
- 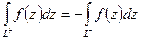 ;
;
- 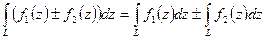 ;
;
- 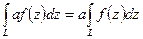 , где
, где 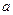 - постоянная;
- постоянная;
- 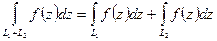 ;
;
- 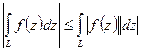 .
.
4.4. Вычисление контурных интегралов от непрерывной функции комплексного переменного:
 2015-06-26
2015-06-26 1713
1713