Алгоритм на псевдокоде. Вычисление хеш-функции для строки S

Вычисление хеш-функции для строки S

Обозначим t – длина строки S

h:=0

DO (i=1,2,…,t)

h:=(h∙256+S_i) mod m

OD

15.2 Метод прямого связывания

Рассмотрим метод устранения коллизий путем связывания в список всех элементов с одинаковыми значениями хеш-функции, при этом необходимо m списков. Включение элемента в хэш-таблицу осуществляется в два действия:

1) вычисление i=H(k)

2) добавление элемента k в конец i -того списка

Поиск элемента также требует два действия:

1) вычисление i=H(k)

2) последовательный просмотр i- того списка.

Пример. Составить хеш-таблицу для строки КУРАПОВА ЕЛЕНА. Будем использовать номера символов в алфавитном порядке. Пусть m =5,

H(k)=ORD (k mod 5)

Вычислим значения хэш-функции для символов строки

H (К)=11 mod 5=1

H (У)=20 mod 5=0

H (Р)=17 mod 5=2

H (А)=1 mod 5=1

H (П)=16 mod 5=1

H (О)=15 mod 5=0

H (В)=3 mod 5=3

H (Е)=6 mod 5=1

H (Л)=12 mod 5=2

H (Н)=14 mod 5=4

Объединим символы с одинаковыми хеш-номерами в один список

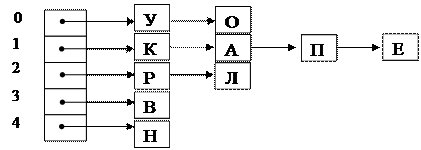Рисунок 62 Хеш-таблица, построенная методом прямого связывания

Оценим трудоемкость поиска в хеш-таблице, построенной методом прямого связывания. Пусть n – количество элементов данных, m – размер хеш-таблицы. Если все ключи равновероятны и равномерно распределены по хеш-таблице, то средняя длина списка будет 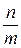. При поиске в среднем нужно просмотреть половину списка. Поэтому C_ср= 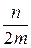. Если n<m, то С_ср<2, т. е. в большинстве случаев достаточно одного сравнения. Объем дополнительной памяти определяется объемом памяти, необходимой для хранения (m+n) указателей. Известно, что трудоемкость поиска с помощью двоичного дерева: С_ср=log n, объем дополнительной памяти – 2 n указателей. Метод прямого связывания становится более эффективным, чем дерево поиска, когда

,

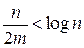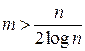
Если n =1000, то при m >50 (m =53) метод прямого связывания более эффективен, чем дерево поиска, причем экономия памяти составит около 4 Кбайт. Можно сэкономить еще больше памяти, если отказаться от списков и размещать данные в самой хеш-таблице.

15.3 Метод открытой адресации

Рассмотрим метод открытой адресации, который применяется для разрешения коллизий при поиске с использованием хеш-функций. Суть метода заключается в последовательном просмотре различных элементов таблицы, пока не будет найден искомый ключ k или свободная позиция. Очевидно, необходимо иметь правило, по которому каждый ключ k определяет последовательность проб, т.е. последовательность позиций в таблице, которые нужно просматривать при вставке или поиске ключа k. Если мы произвели пробы и обнаружили свободную позицию, то ключа k нет в таблице. Таким образом, коллизия устраняется путем вычисления последовательности вторичных хеш-функций:

h₀=h(x)

h₁=h(x)+g(1) ( mod m)

h₂=h(x)+g(2) ( mod m)

h_i=h(x)+g(i) ( mod m)

Самое простое правило для просмотра – просматривать подряд все следующие элементы таблицы. Этот прием называется методом линейных проб, при этом g(i)=i, i =1,2,…, m -1. Недостаток данного метода – плохое рассеивание ключей (ключи группируются вокруг первичных ключей, которые были вычислены без конфликта), хотя и используется вся хеш-таблица.

Если в качестве вспомогательных функций использовать квадратичные, т.е. g(i)=i², i =1,2,…, m -1, то такой способ просмотра элементов называется методом квадратичных проб. Достоинство этого метода – хорошее рассеивание ключей, хотя хеш-таблица используется не полностью.

Утверждение. Если m – простое число, то при квадратичных пробах просматривается по крайней мере половина хеш-таблицы.

Доказательство. Пусть i -ая и j -ая пробы, i<j, приводят к одному значению h, т.е. h_i=h_j. Тогда i ² mod m = j ² mod m

(j² – i²) mod m =0

(j+i)(j-i) mod m =0

(j+i)(j-i) = km

i+j = km/(j-i)

Если m – простое число, то k/(j-i) – целое число больше нуля. В худшем случае k/(j-i) =1, тогда i+j=m и j>m/ 2. (Если m – не простое число, то k/(j-i) не обязательно должно быть целым).

На практике этот недостаток не столь существенен, т.к. m/2 вторичных попыток при разрешении конфликтов встречаются очень редко, главным образом в тех случаях, когда таблица почти заполнена.

Итак, нам нужно вычислять

h₀=h(x)

h_i=(h₀+i²) mod m, i>0

Вычисление h_i требует одного умножения и деления. Покажем, как можно избавиться от этих операций. Произведем несколько первых шагов при вычислении h_i.

h₁=h₀+ 1

h₂=h₀ +4= h₀+ 1+3= h₁ +3 (mod m)

h₃=h₀ +9= h₀ +4+5= h₂ +5 (mod m)

…

Нетрудно видеть, что возникает рекуррентное соотношение:

d₀ =1, h₀=h(x)

h_i+1 = h_i+d_i (mod m)

d_i+1=d_i +2

Поскольку h_i<m, d_i<m, то можно избавиться от деления, заменив его вычитанием h=h-m (см. алгоритм).