Математический аппарат для описания сложных систем

Наиболее широкое распространение получили методы моделирования сложных систем, базирующиеся на результатах теории множеств, основоположником которой является Георг Кантор. Развитие теоретико-множественной концепции в описании систем дали работы А.Н. Колмогорова и группы французских математиков, которые в середине 30-х годов 20-го века выступали под коллективным названием Никола Бурбаки.

Г. Кантор определил множество как «объединение в одно целое объектов, хорошо различимых нашей интуицией или нашей мыслью». Множество обычно обозначают большими латинскими буквами: A, B, C и т.д. Конечное множество может быть задано перечислением его элементов:

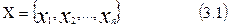
Другой способ задания состоит в указании свойства P(x), которым обладают элементы

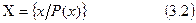
В отличие от неупорядоченных множеств из n элементов (3.1), вводятся упорядоченные множества (кортеж длины n)

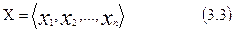
Принадлежность элемента x к множеству X фиксируется записью

Противоположное утверждение

Совокупность элементов, взятых из множества Х, образует новое множество Y, являющееся подмножеством (частью множества) Х. Запись имеет вид

Множества равны, если они состоят из одинаковых элементов.

Специальными видами множеств являются пустое множество Ф, не содержащее ни одного элемента, и множество всех подмножеств заданного множества Х, называемого булеаном Б (х), включая само множество Х и пустое множество Ф.

Для множеств вводятся операции объединения 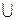, пересечения 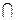, взятие разности \, определяемые указанием свойства Р(х) для элементов множества.

Если 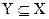, то разность 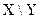называется дополнением относительно Х и обозначается .

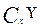Декартово произведение множеств 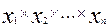определяется как множество таких упорядоченных значений, что первый элемент принадлежит 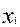, второй 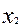и т.д.

Если 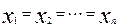, то произведение .

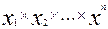Множества Х и Y называют эквивалентными (X~Y), если между их элементами существует взаимно однозначное соответствие, то есть каждому элементу 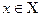соответствует один и только один элемент 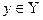и наоборот.

Мощность множества характеризуется числом его элементов (кардинальным числом): car a x = n, car (x) = 2ⁿ.

Весьма важными понятиями в теории множеств являются понятия отношения и отображения. Они связаны с совокупностью правил выделения определенного подмножества элементов из заданного декартова произведения множеств. Рассмотрим бинарное отношение, когда число множеств равно двум.

Бинарным отношением называется всякое подмножество декартова произведения множеств Х и Y, на которых оно задано

Это определение не связывает отношение с содержательными правилами, по которым оно строится, и множество пар может быть получено в принципе как любое подмножество декартовых произведений заданных множеств.

Поэтому, с точки зрения системных приложений, предпочтительнее другое, более развернутое определение, в котором 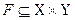рассматривается как график некоторого отношения f. Само же определение формулируется так: бинарным отношением называется тройка 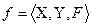, где X и Y – множества, на которых задается отношение f как совокупность правил, выделяющих график F в декартовом произведении X и Y.

Если множества X и Y конечны и содержат соответственно m и n
элементов, то существует ряд способов наглядного представления графика F в виде:

а) сетки с m горизонталями и n вертикалями и помеченными узлами отдельных пересечений, удовлетворяющих правилу ;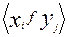

б) матрицы типа m´n с единицами на пересечениях, удовлетворяющих правилу ;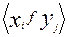

в) стрелочного представления, в котором стрелки соединяют точк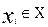и и 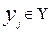в том случае, если имеет место .

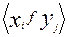При детальном анализе свойств отношений используются символы математической логики.

Бинарные отношения используются в приложениях при установлении соответствия, например, между элементами множества X входных сигналов и элементами множестваY выходных сигналов. Допустим, что однозначное соответствие между элементами этих множеств существует, и существует множество пар элементов 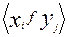, удовлетворяющих f. Тогда речь по существу идет о функциональной зависимости, о функциональном отношении 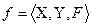, где F- график функции, то есть множество пар, удовлетворяющих закону, устанавливаемому функцией f.

Наиболее употребительная форма записи имеет вид 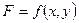. Здесь символом 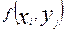обозначают число 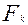, которое в силу закона f соответствует значению пары элементов .

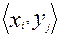В системных исследованиях, когда меру соответствия между элементами множеств выразить трудно из-за отсутствия априорной информации или из-за неопределенности целевой функции, вместо понятия функции вводится более общее понятие отображения из X в Y и соответствующая ему форма записи

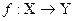или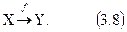

Используются также отношения произвольной арности. Под n-арным отношением понимается конструкция 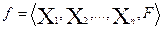, где 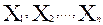- множества, на которых задается отношение как некоторый закон (совокупность правил), выделяющий подмножество 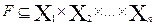- график данного отношения.

При n=1 - отношение унарное, при n=2 - отношение бинарное, при n=3 – отношение тернарное, при n=4 – отношение кватернарное и т.д.

Форма записи при этом

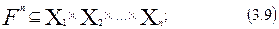
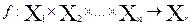- отображение декартова произведения n исходных множеств в множество .

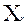Отношения могут устанавливать не только меру соответствия между элементами, но и меру предпочтения, которая позволяет установить превосходство или равноценность сравниваемых элементов. Отношения предпочтения имеют определенный смысл, заложенный в сравниваемых признаках. Они применяются в задачах выбора.