Для построения графика теоретического закона распределения совместно с графиком гистограммы и для проверки согласия по критерию хи-квадрат Пирсона надо заполнить таблицу, знакомую по лекции (см. ниже по тексту, таблица №1). Для построения этой таблицы надо воспользоваться таблицей карман – частота процедуры Гистограмма.
xi – границы интервалов группировки (карманы – получены как результат выполнения процедуры Гистограмма);
mi – количество элементов выборки, попавших в i – ый интервал (частота – получена в результате процедуры Гистограмма);
Таблица №1
| xi | mi | n∙pi | 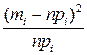 |
| карманы | частота | теоретическая частота | статистика U |
| x1 | m1 | n∙p1 | 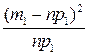 |
| x2 | m2 | n∙p2 | 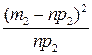 |
| … | … | … | … |
| xk | mk | n∙pk | 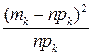 |
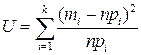 |
Для построения этой таблицы в Excel к столбцам Карман и Частота процедуры Гистограмма надо добавить столбцы n∙pi и 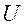 , где в ячейках столбца
, где в ячейках столбца 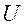 будет находиться статистика
будет находиться статистика 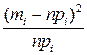 (как показано на рис. 6).
(как показано на рис. 6).
pi – теоретическая вероятность попадания элементов выборки в i – ый интервал группировки для принятой гипотезы о нормальном распределении генеральной совокупности равна
pi = P (xi-1 < X < xi) = F(xi) – F(xi-1).
n∙pi – теоретическая, ожидаемая частота попадания элементов выборки в i – ый интервал группировки для принятой гипотезы о нормальном распределении генеральной совокупности.
В Excel эту величину можно вычислить, воспользовавшись функцией НОРМРАСП.
n∙pi = НОРМРАСП(xi; среднее; стандартное_откл; 1)· n –
– НОРМРАСП(xi-1; среднее; стандартное_откл; 1) · n.
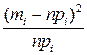 – статистика, являющаяся мерой расхождения между значениями эмпирической и теоретической плотности распределения;
– статистика, являющаяся мерой расхождения между значениями эмпирической и теоретической плотности распределения;
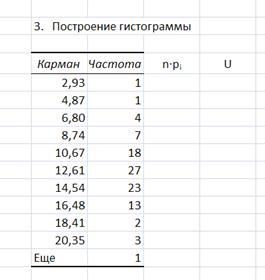
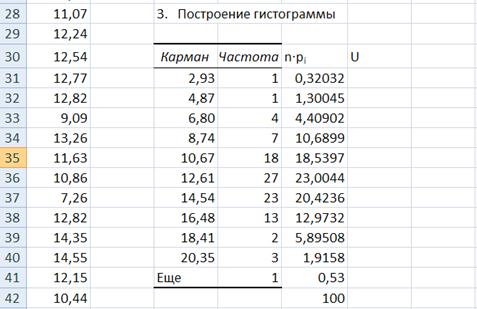
Рис. 6. Подготовительная таблица для построения графика теоретической плотности нормального распределения.
Замечание. Функцию НОРМРАСП вызывается следующим образом. В главном меню Excel выбирается закладка Формулы → Вставить функцию (или щелкните в строке формул значок fx) → в диалоговом окне Мастер функций – шаг 1 из 2 в категории Статистические → НОРМРАСП. ОК.
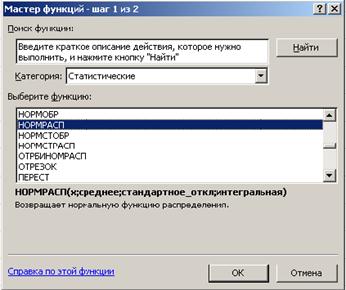
Рис. 7. Окно Мастер функций для выбора функции НОРМРАСП из категории Статистические.
В раскрывшемся окне Аргументы функции НОРМРАСП заполните поля ввода как показано далее на рис. 10.
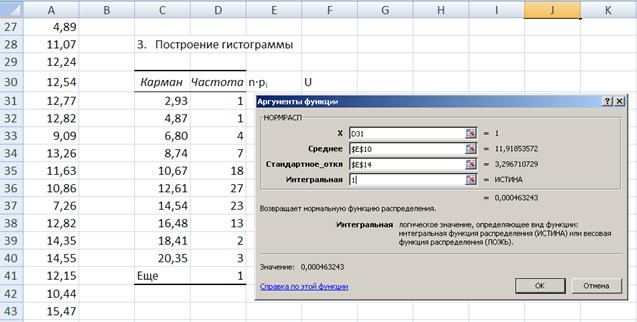
Рис. 8. Окно ввода параметров для получения функции нормального распределения
В поле X вводится адрес ячейки, в которой находится граница интервала группировки.
В поле Среднее вводится адрес ячейки, в которой находится среднее значение выборки, полученное при выполнении процедуры Описательная статистика – E$10$.
В поле Стандартное_откл вводится адрес ячейки, в которой находится значение стандартного отклонения выборки, полученное при выполнении процедуры Описательная статистика – E$14$.
В поле Интегральная введите единица 1. Единица в поле Интегральная означает вычисление функции распределения F(x). ОК.
 1. В ячейку E31 внесите формулу
1. В ячейку E31 внесите формулу 
для вычисления значения функции нормального распределения F (x1 = 2,93) = P (– ∞ < X ≤ x1), умноженного на число наблюдений n. В рассматриваемом примере n =100. В ячейку E31 будет получено теоретическое (ожидаемое) число случайных величин, попавших в интервал 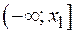 , n∙pi = F (x1)∙100,=НОРМРАСП(C31;E$10$;E$14$;1)*100 (как показано на рис. 9).
, n∙pi = F (x1)∙100,=НОРМРАСП(C31;E$10$;E$14$;1)*100 (как показано на рис. 9).
E10 – среднее значение, E14 – стандартное отклонение, взятые из таблицы Описательная статистика.

2. В ячейку E32 поместите формулу для вычисления теоретического (гипотетического) числа случайных величин, попавших в интервал 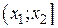 :
:
n∙p2 = n ∙ [ F (x2) – F (x1)] = n ∙ [ P (x1 < X ≤ x2)] = n ∙ [ P (2,93 < X ≤ 4,87)],
где p2 = F (x2) – F (x1) = P (x1 < X ≤ x2) = P (2,93 < X ≤ 4,87) - теоретическая вероятность попадания нормально распределенных случайных величин в промежуток 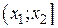 .
.
В Excel в строку формул необходимо поместить формулу:

=(НОРМРАСП(C32;$E$10;$E$14;1)*100 –
– НОРМРАСП(C31;$E$10;$E$14;1))*100
Заполните диапазон ячеек Е33:Е40 результатами вычисления этой формулы, используя маркер заполнения, чтобы получить в ячейках 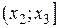 ,
, 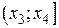 , …,
, …, 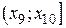 теоретическое (ожидаемое) число случайных величин, попавших в каждый частный интервал.
теоретическое (ожидаемое) число случайных величин, попавших в каждый частный интервал.

 |

 |

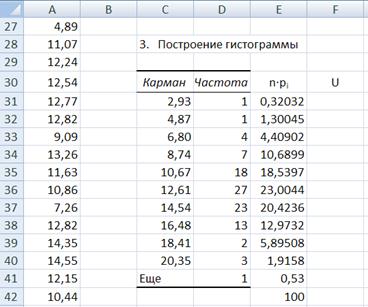

Рис. 9. Столбец n∙pi (E31;E41) содержит результаты вычисления теоретических значений числа случайных величин попавших в каждый частичный интервал (карман) n∙pi
 3. В ячейку E41 поместите формулу
3. В ячейку E41 поместите формулу  для вычисления теоретического (гипотетического) числа случайных величин, попавших в промежуток (x10; ∞):
для вычисления теоретического (гипотетического) числа случайных величин, попавших в промежуток (x10; ∞):
P (x10 < x < ∞) = 1 – P (– ∞ < x ≤ x10) = 1 – F (x10) – вероятность попадания нормально распределенных случайных величин в промежуток (x10; ∞).
В Excel в строку формул необходимо поместить формулу:
=(1 – НОРМРАСП(C40;E$10$;E$14$;1))*100
В результате всех этих операций выводится таблица (рис. 9).
Для проверки правильности вычислений просуммируйте числа в ячейках столбца E31:E41. В ячейке Е42 показана сумма содержимого ячеек Е31:Е40. Она должна быть равна n = 100.
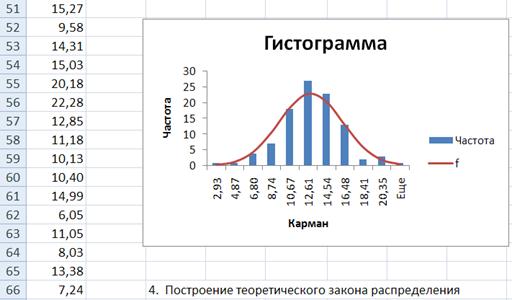
В графике Гистограмма частот добавьте кривую нормального (теоретического) распределения, как это вы умеете делать.
Щелкните правой кнопкой мыши по столбику гистограммы, в появившемся меню выберите: Выбрать данные… → Добавить → заполнить поля ввода Имя ряда: f, Значения: введите массив значений n∙pi, (или Имя ряда:, Значения X:, Значения Y) ОК, ОК.
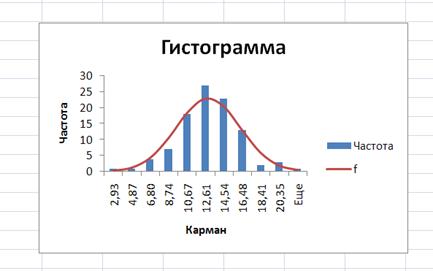
Рис. 10. Графики гистограммы эмпирических и теоретических частот, позволяющие по виду графиков выбрать в качестве гипотезы H0 нормальное распределение.
5. Проверка согласия эмпирического и теоретического законов распределения по критерию хи-квадрат Пирсона (b = 0,95)
Для того чтобы сохранить графики гистограммы эмпирических и теоретических частот в красивом виде необходимо скопировать таблицу на рис. 9 Карман – Частота – n∙pi – U в другое место таблицы.
Скопируйте таблицу Карман – Частота – n∙pi – U в свободные ячейки листа Excel, для чего, верхний левый угол копии разместите, например, в ячейке C75.
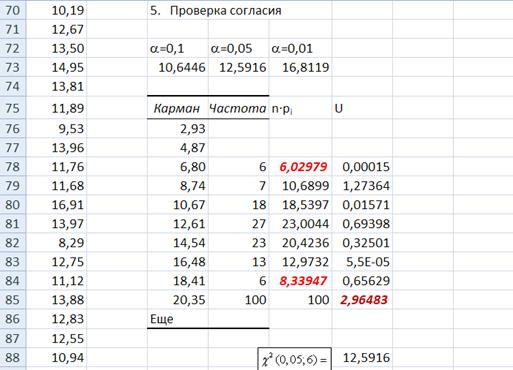
Для вычисления статистики 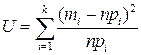 необходимо выполнить условие – в каждом кармане должно быть не менее 5 элементов выборки (n∙pi ≥ 5) для теоретических значений распределения частот. Объединим (просуммируем) три верхние ячейки (просуммируем ячейки E76, E77 и E78, их сумма дает величину больше 5, а именно 6,02979) и три нижние ячейки (просуммируем ячейки E84, E85 и E86, их сумма дает величину 8,33947), столбца n∙pi, содержащего теоретические частоты.
необходимо выполнить условие – в каждом кармане должно быть не менее 5 элементов выборки (n∙pi ≥ 5) для теоретических значений распределения частот. Объединим (просуммируем) три верхние ячейки (просуммируем ячейки E76, E77 и E78, их сумма дает величину больше 5, а именно 6,02979) и три нижние ячейки (просуммируем ячейки E84, E85 и E86, их сумма дает величину 8,33947), столбца n∙pi, содержащего теоретические частоты.
Суммируемые ячейки на рис. 11 выделены красным курсивом.
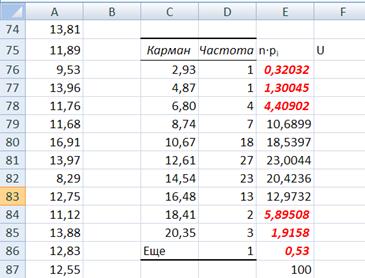
Рис. 11. Верхние ячейки E76, E77 и E78, выделенные для суммирования, и нижние ячейки E84, E85 и E86, выделенные для суммирования.
В результате после суммирования получится таблица рис. 12.
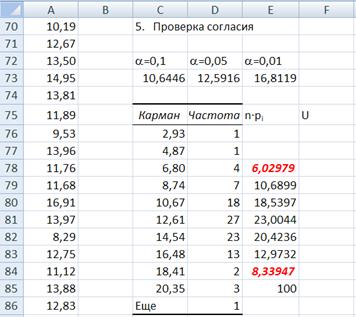
Рис. 12. В столбце n∙pi объединены ячейки E76, E77 и E78 (результат суммирования – в ячейке E78) и ячейки E84, E85 и E86 (результат суммирования – в ячейке E84).
Объедините три верхние ячейки D76, D77 и D78 и три нижние ячейки D84, D85 и D86 столбца Частота, содержащего эмпирические (опытные) частоты.
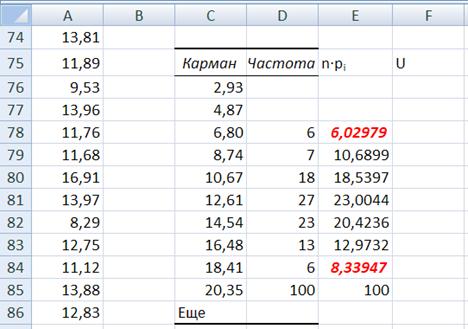
Рис. 13. В столбце Частота объединены ячейки D76, D77 и D78 (результат суммирования – в ячейке D78) и ячейки D84, D85 и D86 (результат суммирования – в ячейке D84).
Для проверки правильности проведенных операций суммирования просуммируйте столбцы D78 – D84 и столбцы E78 – E84, результат должен быть равен объему выборки n = 100.
В ячейку F78 столбца помеченного именем U введите формулу 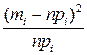 , в строку формул введите формулу =(D78-E78)^2)/E78,
, в строку формул введите формулу =(D78-E78)^2)/E78,  и скопируйте ее в ячейки F79 – F84.
и скопируйте ее в ячейки F79 – F84.
В ячейке F85 получите сумму 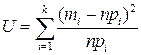 содержимого ячеек F78;F84.
содержимого ячеек F78;F84.
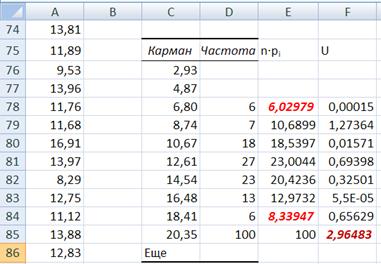
Рис. 14. Таблицы с результатами вычисления статистики
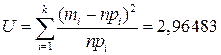
В ячейке F85 получено значение статистики 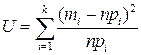 ,
,
U = 2,96483.
Критическое значение статистики U, которая имеет распределение 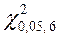 для уровня значимости a = 1 - b = 0,05, с шестью (число частичных интервалов – 1 – число параметров, в рассматриваемом примере 9 – 1 – 2 = 6) степенями свободы, определяется при помощи функции ХИ2ОБР.
для уровня значимости a = 1 - b = 0,05, с шестью (число частичных интервалов – 1 – число параметров, в рассматриваемом примере 9 – 1 – 2 = 6) степенями свободы, определяется при помощи функции ХИ2ОБР.
Функцию ХИ2ОБР вызывается следующим образом. В главном меню Excel выбирается закладка Формулы → Вставить функцию → в диалоговом окне Мастер функций – шаг 1 из 2 в категории Статистические → ХИ2ОБР. ОК.
В диалоговом окне Аргументы функции ХИ2ОБР заполните поля как показано на рис. 15, предварительно выбрав ячейку для результата вычисления функции, например F88.
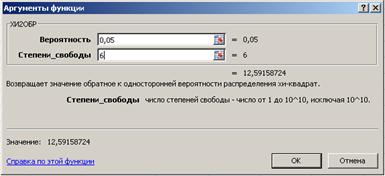
Рис. 15. Диалоговое окно функции ХИ2ОБР с заполненными полями ввода
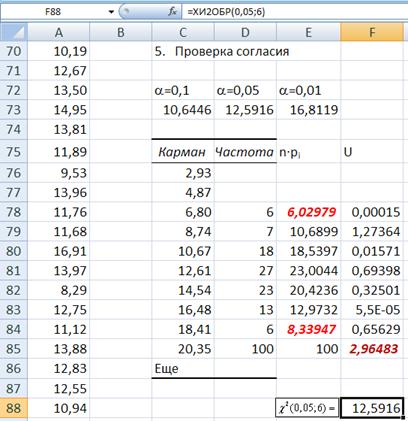
Рис. 16. Таблица с окончательными результатами вычисления статистики
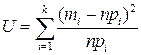 и критического значения
и критического значения 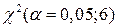 = 12.5916
= 12.5916
Значение статистики U = 2,96483 оказалось меньше критического значения 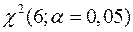 = 12.5916, как это видно из таблицы.
= 12.5916, как это видно из таблицы.
Вывод. Следовательно, гипотеза, состоящая в том, что генеральная совокупность подчиняется нормальному закону распределения, принимается.
Теперь можно использовать принятый гипотетический закон распределения – закон распределения генеральной совокупности для вычисления вероятностей попадания исследуемой случайной величины в заданный интервал.
7. Вычисление вероятности попадания исследуемой случайной величины в заданные интервалы (c = 10, d = 15)
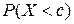 =,
=, 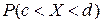 =,
=, 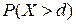 =.
=.
Вычисления выполнить в Excel. Используя функцию НОРМРАСП.
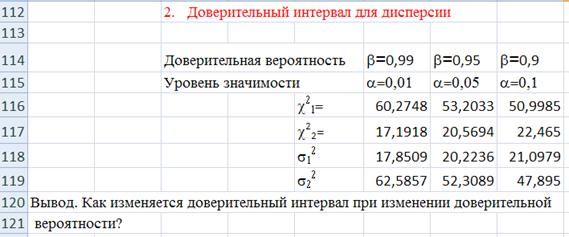
8. Доверительные интервалы для заданной доверительной вероятности b = 0,99, b = 0,95, b = 0,9.

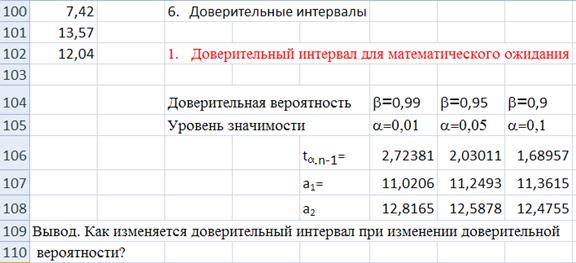
1. Доверительный интервал для неизвестного математического ожидания при неизвестной дисперсии
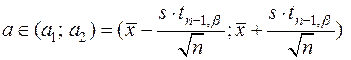 ,
,
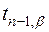 – критическая точка распределения Стьюдента с n – 1 числом степеней свободы и уровнем значимости a = 1 - b
– критическая точка распределения Стьюдента с n – 1 числом степеней свободы и уровнем значимости a = 1 - b

2. Доверительный интервал для неизвестного дисперсии
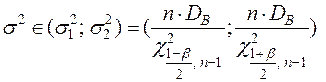 ,
,
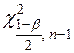 и
и 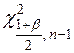 – критическая точка распределения
– критическая точка распределения 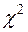 с n – 1 числом степеней свободы и уровнем значимости
с n – 1 числом степеней свободы и уровнем значимости 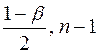
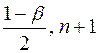 .
.
Пример вычислений в Excel приведен в приложении 1.
Приложение 1
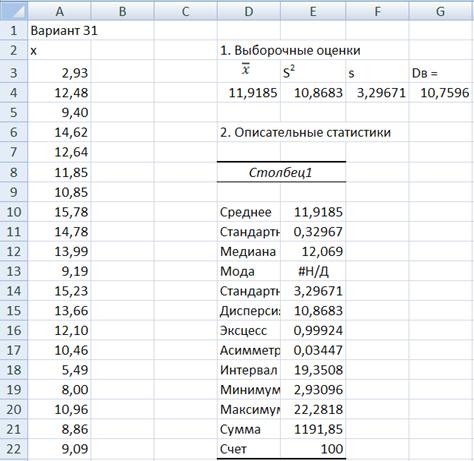
…. …… …… ….. ….
… … … … … … … …
… … … … … … … …

…. …. … … …. …. …. …
 2015-01-30
2015-01-30 7662
7662