Определение 1.1. Степенным рядом называется функциональный ряд вида
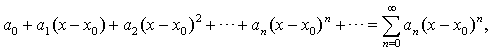 (1.1) где a0, a1, a2, …,an,…, а также x0 – постоянные числа. Точку x0 называют центром степенного ряда.
(1.1) где a0, a1, a2, …,an,…, а также x0 – постоянные числа. Точку x0 называют центром степенного ряда.
Сначала рассмотрим степенные ряды с центром 0, т.е. ряды вида
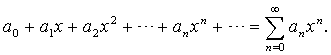 (1.2)
(1.2)
Такой ряд всегда сходится при x =0 и, значит, его область сходимости есть непустое множество.
Теорема 1.1. (теорема Абеля). Если степенной ряд (1.2) сходится при некотором 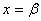 , где
, где  -число, не равное нулю, то он сходится абсолютно при всех значениях x таких, что
-число, не равное нулю, то он сходится абсолютно при всех значениях x таких, что 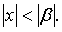 Наоборот, если ряд (12) расходится при
Наоборот, если ряд (12) расходится при 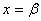 , то он расходится при всех значениях x таких, что
, то он расходится при всех значениях x таких, что 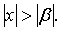
Доказательство. Пусть числовой ряд
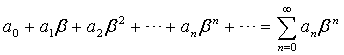 (1.3)
(1.3)
сходится. Поэтому 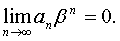 Но любая последовательность, имеющая предел, ограничена, значит, существует такое число M, что
Но любая последовательность, имеющая предел, ограничена, значит, существует такое число M, что 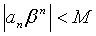 для всех n =0,1,2,…
для всех n =0,1,2,…
Рассмотрим теперь ряд
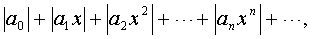 (1.4)
(1.4)
предполагая, что 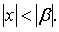 Так как
Так как 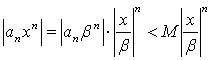 и при этом
и при этом 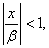 то члены ряда (3.4) не превосходят соответствующих членов сходящегося ряда
то члены ряда (3.4) не превосходят соответствующих членов сходящегося ряда

(геометрической прогрессии). Следовательно, ряд (1.4) сходится, а ряд (1.2) абсолютно сходится.
Предположим теперь, что ряд (1.3) расходится, а ряд (1.2) сходится при 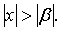 Но тогда из сходимости ряда (1.2) следует сходимость и ряда (1.3), что противоречит предположению. Теорема доказана.
Но тогда из сходимости ряда (1.2) следует сходимость и ряда (1.3), что противоречит предположению. Теорема доказана.
Теорема Абеля позволяет дать описание области сходимости степенного ряда.
Теорема 1.2. Для степенного ряда (1.2) возможны только три случая:
1) ряд сходится в единственной точке x=0;
2) ряд сходится при всех значениях x;
3) существует такое R>0, что ряд сходится при всех значениях x, для которых 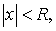 и расходится при всех x, для которых
и расходится при всех x, для которых 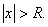
Определение 1.2. Интервал (-R,R), где число R определено в теореме 1.2, называется интервалом сходимости ряда (1.2), а число R – радиусом сходимости этого ряда.
Понятие радиуса сходимости будет распространяться на все три случая в теореме (3.2): для этого в случае 1 условимся считать R =0, а в случае 2 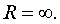
На практике радиус сходимости степенного ряда чаще всего определяют с помощью признака сходимости Даламбера. Предположим, что все коэффициенты ряда (1.2) отличны от нуля и существует предел 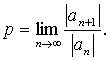 Тогда радиус сходимости находится по формуле
Тогда радиус сходимости находится по формуле 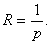
Действительно, в силу признака Даламбера ряд
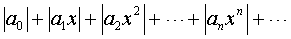
сходится, если число
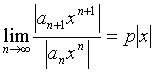
меньше 1, и расходится, если этот предел больше 1. Иначе говоря, ряд сходится для всех x таких, что  и расходится при
и расходится при 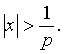 Это и означает, что число
Это и означает, что число 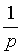 является радиусом сходимости ряда (1.2).
является радиусом сходимости ряда (1.2).
Пример 1.1. Найти область сходимости ряда
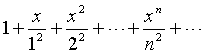
Решение. 
Следовательно, радиус сходимости есть 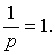 Ряд сходится при
Ряд сходится при
– 1 <x< 1и расходится при 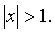 В точках x =1 и x =-1 ряд также сходится.
В точках x =1 и x =-1 ряд также сходится.
Итак, область сходимости ряда – отрезок 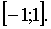
 2015-01-07
2015-01-07 8360
8360
