Здесь возможны три случая:.
1. Область сходимости и состоит только из одной точки х=0. Другими словами, ряд расходится для всех значений х кроме одного. Этот случай может быть иллюстрирован рядом:
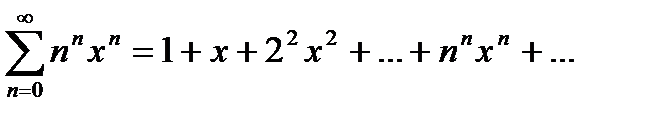
Действительно, если х фиксировано и х>О, то, начиная с достаточно большого n, будет 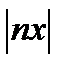 >1, откуда вытекает неравенство
>1, откуда вытекает неравенство 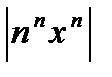 >1 означающее, что общий член ряда не стремится к нулю.
>1 означающее, что общий член ряда не стремится к нулю.
2. Область сходимости состоит из всех точек оси ОХ, другими словами, ряд сходится при всех х. Рассмотрим ряд:
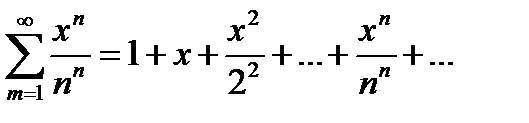
Для любого х, с.достаточно большого п, будет.  Так как:
Так как:
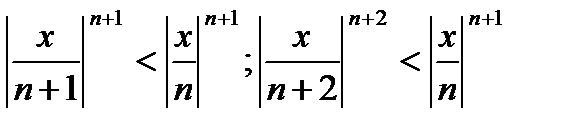 и т.д.,
и т.д.,
то начиная с номера n, члены ряда по абсолютной величине будут меньше членов сходящейся геометрической прогрессии, следовательно, при всяком х ряд сходится.
3. Область сходимости состоит больше чем из одной точки оси ОХ, причем есть точки оси, не принадлежащие области сходимости. Например, ряд:
1+х+х2 +...+хn+..,
представляющий геометрическую прогрессию со знаменателем х, сходится при |х|<1 и расходится при |x|>l.
В третьем случае на числовой оси наряду с точками сходимости ряда имеются и точки расходимости.
|
|
|
Из теоремы Абеля и ее следствия вытекает, что все точки сходимости расположены от начала координат не дальше, чем любая из точек расходимости. Совершенно ясно, что точки сходимости будут целиком заполнять некоторый интервал с центром в начале координат.
Таким образом, можно сказать, что для каждого степенного ряда, имеющего как точки сходимости, так и точки расходимости, существует такое положительное число R, что для всех х, по модулю меньших R(|x|<R),ряд абсолютно сходится, а для всех х, по модулюбольших R(|x|>R), ряд расходится.
Что касается значений x=R и x=-R, то здесь могут осуществляться различные возможности: ряд может сходится в обеих точках, или только в одной из них, или ни в одной.
При этом ряд может сходиться как абсолютно, так и условно. Определение 19.3 Радиусом сходимости степенного ряда (19.2) называется такое число R, что для всех х, \х\ < R степенной ряд сходится, а для всех 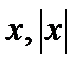 >R, расходится. Интервал от х=-R до x=R называется интерваломсходимости. Условия для рядов, расходящихся при всех x кроме х=0, считать R=0, а для рядов, сходящихся при всех х, считать R=0.
>R, расходится. Интервал от х=-R до x=R называется интерваломсходимости. Условия для рядов, расходящихся при всех x кроме х=0, считать R=0, а для рядов, сходящихся при всех х, считать R=0.
Для степенных рядов вида (19.5) все сказанное выше остается в силе с той только разницей, что теперь центр интервала сходимости будет интервал (х0 - R,x0 + R).
Укажем способ определения радиуса сходимости степенного ряда. Пусть имеем ряд:
а0 +alx+a2x2 +... + an-1xn-1+anxn +...
Рассмотрим ряд, составленный из абсолютных величин его членов:
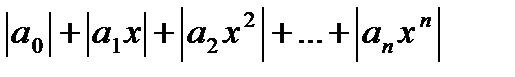
Для определения сходимости последнего ряда применим признак Даламбера. Допустим, что существует предел:
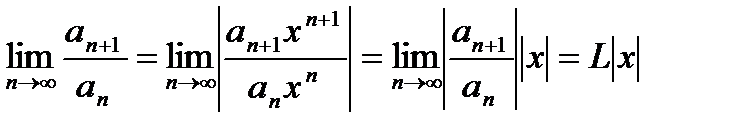
Тогда по признаку Даламбера ряд (19.2) сходится, если L \х\ < 1. то есть если |x| < 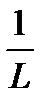 , и расходится, если L \х\ > 1,то есть если |х| >
, и расходится, если L \х\ > 1,то есть если |х| > 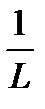 .
.
|
|
|
Следовательно, ряд (19.2) сходится абсолютно при 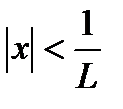 . Если
. Если 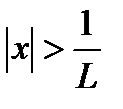
то 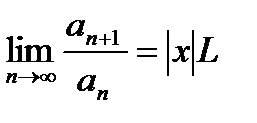 > 1, и ряд (19.2) расходится, причем его общий член
> 1, и ряд (19.2) расходится, причем его общий член
данного степенного ряда (19.2) не стремится к нулю, а это значит, на основании необходимого признака сходимости, что этот степенной
ряд расходится (при 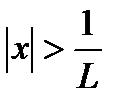 ). Из предыдущего следует, что интервал
). Из предыдущего следует, что интервал 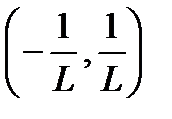 есть интервал сходимости степенного ряда (19.2), то есть:
есть интервал сходимости степенного ряда (19.2), то есть:
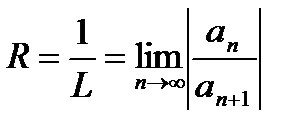 (19.4)
(19.4)
илисогласно радикального признака Коши:
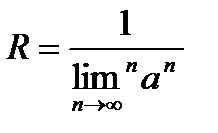 (19.5)
(19.5)
Теорема 19.2. Если существует предел
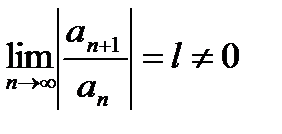 , то интервал сходимости ряда
, то интервал сходимости ряда 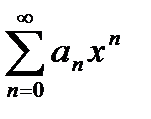 будет
будет 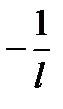 <х<
<х< 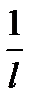 .
.
Поясним сказанное на конкретных примерах.
 2015-03-07
2015-03-07 1155
1155








