Рассмотрим задачу Коши для уравнения первого порядка:
u /(x) = f (x, u(x)), x 0 ≤ x ≤ x max, u (x 0) = u 0. (3)
В окрестности точки x 0 функцию u (x) разложим в ряд Тейлора:
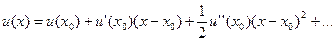 (4)
(4)
 Идея этого и последующих методов основывается на том, что если f (x, u) имеет q непрерывных производных, то в разложении можно удержать члены вплоть до O (h q+1), при этом стоящие в правой части производные можно найти, дифференцируя (3) требуемое число раз. В случае метода Эйлера ограничимся только двумя членами разложения.
Идея этого и последующих методов основывается на том, что если f (x, u) имеет q непрерывных производных, то в разложении можно удержать члены вплоть до O (h q+1), при этом стоящие в правой части производные можно найти, дифференцируя (3) требуемое число раз. В случае метода Эйлера ограничимся только двумя членами разложения.
Пусть h – малое приращение аргумента. Тогда (4) превратится в
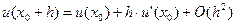 .
.
Так как в соответствии с (3) u /(x 0) = f (x 0, u 0), то 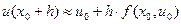 .
.
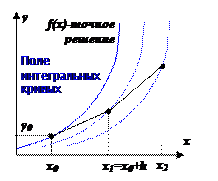
Теперь приближенное решение в точке x 1 = x 0 + h можно вновь рассматривать как начальное условие, т.е. организуется расчет по следующей рекуррентной формуле:
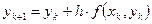 (5),
(5),
где y 0 = u 0, а все y k – приближенные значения искомой функции (см. рисунок). В методе Эйлера происходит движение не по интегральной кривой, а по касательной к ней. На каждом шаге касательная находится уже для новой интегральной кривой (что и дало название методу – метод ломаных), таким образом ошибка будет возрастать с отдалением x от x 0.
|
|
|
При 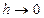 приближенное решение сходится к точному равномерно с первым порядком точности. То есть, метод дает весьма низкую точность вычислений: погрешность на элементарном шаге h составляет ½ h 2 y //(½(x k + x k+1)), а для всей интегральной кривой порядка h 1. При h = const для оценки апостериорной погрешности может быть применена первая формула Рунге, хотя для работы метода обеспечивать равномерность шага в принципе не требуется.
приближенное решение сходится к точному равномерно с первым порядком точности. То есть, метод дает весьма низкую точность вычислений: погрешность на элементарном шаге h составляет ½ h 2 y //(½(x k + x k+1)), а для всей интегральной кривой порядка h 1. При h = const для оценки апостериорной погрешности может быть применена первая формула Рунге, хотя для работы метода обеспечивать равномерность шага в принципе не требуется.
Метод Эйлера легко обобщается для систем ОДУ. При этом общая схема процесса (5) может быть записана так:
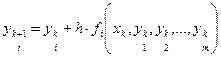 (6),
(6),
где i = 1…m – число уравнений, k – номер предыдущей вычисленной точки.
 2015-01-07
2015-01-07 768
768








