Основные понятия теории числовых рядов

Определение 1. Пусть задана некоторая бесконечная последовательность чисел

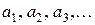(1)

Составленный из этих чисел символ

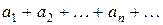(2)

называется бесконечным рядом, а сами числа (1) – членами ряда.

Вместо (2), пользуясь знаком суммы, часто пишут так:

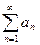; (2а)

показатель 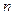пробегает здесь все значения от 1 до 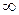. Нумерацию членов ряда иногда начинают не с единицы, а с нуля или же с какого-либо натурального числа, большего единицы.

Станем последовательно складывать члены ряда, составляя суммы

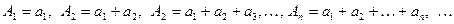(3)

Определение 2. 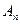называют 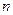-ой частичной суммой ряда (2). Конечный или бесконечный предел 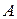последовательности частичных сумм 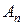называют суммой ряда (2) и пишут

,

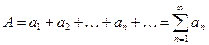придавая тем самым символу (2) или (2а) числовой смысл. Если ряд имеет конечную сумму, то его называют сходящимся, в противном же случае (т.е. если сумма равна 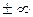, либо же суммы вовсе нет) – расходящимся.

Пример 1. Простейшим примером бесконечного ряда является геометрическая прогрессия:

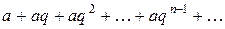
При 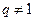имеем 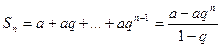. Если знаменатель прогрессии 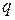будет по абсолютной величине меньше 1, то последовательность 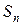имеет конечный предел 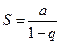, т.е. геометрическая прогрессия в этом случае сходится и ее сумма равна .

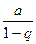При 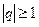та же прогрессия дает пример расходящегося ряда. Действительно, если 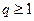, то прогрессия имеет сумму, равную 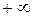или 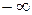, в зависимости от того, будет ли 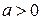или меньше нуля. В том случае, когда 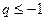, суммы нет вовсе.

2) Ряд 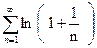расходится, но имеет сумму, равную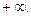

2) Основные теоремы теории числовых рядов.

Определение 1. Если в ряде

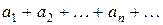(1)

отбросить первые 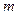членов, то получится ряд

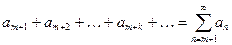, (2)

называемый остатком ряда (1) после 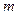–го члена.

Теорема 1. Если сходится ряд (1), то сходится и любой из его остатков (2); обратно, из сходимости остатка (2) вытекает сходимость исходного ряда (1).

Из этой теоремы следует, что отбрасывание конечного числа начальных членов ряда или присоединение в начале нескольких новых членов не отражается на поведении ряда

(в смысле сходимости или расходимости).

Сумму ряда (2), если он сходится, обозначим через 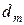, указывая значком 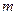, после какого члена берется остаток.

Теорема 2. Если ряд (1) сходится, то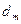

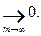
Теорема 3. Если члены сходящегося ряда (1) умножить на один и то же множитель 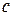, то его сходимость не нарушится (а сумма лишь умножится на ).

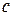Теорема 4. Два сходящихся ряда 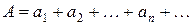и 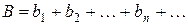можно почленно складывать (или вычитать), так что ряд 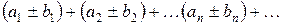также сходится, и его сумма равна, соответственно, .

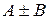Теорема 5(необходимое условие сходимости числовых рядов). Общий член 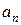сходящегося ряда стремится к нулю.

Замечание1. Общий член расходящегося ряда 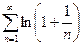стремится к нулю. Таким образом, стремление общего члена к нулю есть условие необходимое, но не достаточное.