Тема 1. Перестановки как абстрактный тип данных

Представление перестановок в естественной форме.

Перестановкой конечного множества X называется некоторое расположение его элементов в ряд. Будем считать X ={1,...,n}, а множество всех перестановок этого множества обозначим S_n.

Пусть f Î S _n, f естественно отождествить с последовательностью <a₁... a_n>, где a_i= f (i). Это приводит к следующему представлению перестановок: f: array [1..n] of 1..n; f(i)=a_i,которое в дальнейшем будем называть естественным.

На языке Паскаль представление абстрактного типа данных требует соответствующего описания типа и некоторой логической функции, проверяющей справедливость необходимых соотношений между значениями, из которых структурирован этот абстрактный тип. Такую функцию в дальнейшем будем называть верификационной функцией этого представления абстрактного типа.

Для перестановок в естественной форме описание типа выглядит так:

tpe= array [1..n] of 1..n; {*}

где n - глобальная константа, определяющая порядок перестановки, а ее верификационная функция имеет вид

function TYPEE (var f: tpe): Boolean;

var a: array [1..n] of Boolean;

i: integer { i<=n+1 };

Begin

for i:=1 to n do a[i]:=true;

i:=1;

while (i<=n) and a[f[i]] do

begin a[f[i]]:=false; i:=i+1 end;

TYPEE:=i=n+1

end;

Комментарий. Булевская функция TYPEE принимает значение true только в том случае, если все значения элементов f попарно различны между собой. Принадлежность значений элементов f диапазону 1..n обеспечена непосредственно описанием типа tpe.

Замечания. 1. Функция TYPEE имеет временную сложность O (n).

2. В дальнейшем принадлежность значения массива абстрактному типу данных - перестановка размерности n, представленная в естественной форме будет обозначаться идентификатором типа TPE, который будет использоваться при указании типа параметров процедур предлагаемых алгоритмов. Другими словами, идентификатор типа TPE, используемый в качестве описания типа параметра процедуры обозначает, что для передаваемого значения функция TYPEE вырабатывает значение true. В случае, если значение входного параметра не удовлетворяет истинности функции TYPEE, корректность процедуры не гарантирована.

Рассмотрим над перестановками часто встречающиеся в алгебре операции: суперпозиция, вычисление обратной перестановки и определение четности перестановки.

Определение. Пусть f = <a₁ a₂... a_n>, g = <b₁ b₂... b_n>. Тогда перестановку g×f = g(f) = <c₁ c₂... c_n>, где c[i] = b[a_i], для i=1,...,n называют суперпозицией перестановок f и g; а перестановку f^-1 равную <d₁ d₂... d_n> так, что d[f_i]=i для i=1,...,n, называют обратной для f.

Упражнение. Докажите, что для любой перестановки f справедливо f×f ^-1 = f ^-1×f= e = <1... n>.

В курсе алгебры обычно четность перестановки определяется через понятие инверсии элементов. Пусть f=<a₁ a₂... a_n>; говорят, что значения a_i и a_j, i,j=1,...,n, образуют инверсию, если из i<j следует a_i>a_j. Перестановку называют четной, если число инверсий в ней четно, и нечетной в противном случае. Четность перестановки может быть также определена как булевская функция, истинная для четных перестановок и ложная в противном случае; либо как функция знака перестановки sign(f)=(-1)^J(f), где J(f) - число инверсий в перестановке f. Относительно операции суперпозиции перестановки образуют группу, которая называется симметрической группой степени n, обозначается S_n, при этом e единица группы.

Рассмотрим алгоритмы реализации этих операций для перестановок в естественном представлении на языке Паскаль.

СУПЕРПОЗИЦИЯ. Алгоритм, реализующий суперпозицию перестановок непосредственно через определение, выглядит так:

procedure S(f:TPE; var g:TPE; var p:TPE);

var i:1..n;

begin for i:=1 to n do p[i]:=f[g[i]] end;

Замечания. 1. Алгоритм имеет временную сложность О (n).

2.Вызов параметра f как значения обусловлен тем, что значения f в общем случае должны быть сохранены до конца работы алгоритма.

ОБРАТНАЯ ПЕРЕСТАНОВКА. Алгоритм построения обратной перестановки p=f^-1 непосредственно по определению выглядит так:

procedure O(f: TPE; var p: TPE);

var i:1..n;

begin for i:=1 to n do p[f[i]]:=i end;

Замечание. Алгоритм имеет временную сложность O (n).

Представленный алгоритм для своей работы копирует перестановку f. Возникает вопрос, существует ли алгоритм трудоемкости O (n), формирующий обратную перестановку непосредственно на месте заданной. Ответ на него утвердителен:

procedure O1(var f: TPE);

var i, j, k, m:1..n; a: array [1..n] of Boolean ;

begin

for i:=1 to n do a[i]:=true;

for i:= 1 to n do

if a[i] then

begin j:=f[i]; a[i]:=false; k:=i; {1}

while j<>i do

begin m:=f[j]; f[j]:=k; k:=j; j:=m; a[k]:=false {2}

end;

f[i]:=k {3}

end;

end {4};

Тест f=<5 7 3 1 6 4 2>

{1} i=1 j=5 a[1]=false k=1 m – не определено

{2} m=6 f[5]=1 k=5 j=6 a[5]=false

{2} m=4 f[6]=5 k=6 j=4 a[6]=false

{2} m=1 f[4]=6 k=4 j=1 a[4]=false

{3} f[1]=4

{1} i=2 j=7 a[2]=false k=2 m=1

{2} m=2 f[7]=2 k=7 j=2 a[7]=false

{3} f[2]=7

{1} i=3 j=3 a[3]=false k=3 m=2

{3} f[3]=3

{4} f=<4 7 3 6 1 5 2>

<5 7 3 1 6 4 2>^.<4 7 3 6 1 5 2>=<1 2 3 4 5 6 7>

Доказательство правильности реализации алгоритма основано на том, что перестановки f и f^-1 имеют взаимосвязанные структуры при разложении их на циклы.

Пример. Разложение перестановки на циклы.

f=<5 7 3 1 6 4 2>

1à5à6à4

2à7

Каждый цикл выписан на отдельной строчке. Внутри цикла следующим выписывается элемент перестановки являющейся образом в f текущего, т. е. xàf(x). Образ последнего элемента совпадает с первым. В этом примере первым в каждом цикле выписан элемент с наименьшим номером внутри цикла, a циклы расположены в порядке возрастания первых элементов.

Для того чтобы получить разложение на циклы обратной для f перестановки, достаточно перевернуть “стрелочки” в каждом цикле разложения f в обратную сторону.

Пример. Разложение на циклы обратной перестановки.

f ^-1=<5 7 3 1 6 4 2>^-1=<4 7 3 6 1 5 2>

1à4à6à5

2à7

Упражнение. Докажите свойство взаимосвязи разложений на циклы f и f^-1 для произвольной перестановки из S_n.

В приведенном алгоритме массив a служит для пометки включенных в циклы элементов f. В каждом цикле первым выбирается элемент, имеющий наименьший номер (второй оператор цикла типа for). Обход каждого цикла с переориентацией стрелок осуществляется оператором цикла типа while.

ЧЕТНОСТЬ ПЕРЕСТАНОВКИ. Алгоритм вычисления четности перестановки непосредственно по определению может быть представлен следующем образом:

function Ч(var. f: TPE): boolean;

var i,j:1..n; s:boolean:

begin s:=true;

for i:=2 to n do

for j:=1 to i-1 do

if f[j]>f[i] then s:= not s;

Ч:=s

end;

Этот алгоритм имеет временную вычислительную сложность О (n²). Однако оказывается, что существует алгоритм определения четности перестановки со сложностью О (n). Такой алгоритм также строится на анализе свойств циклической структуры перестановки на основе следующей теоремы:

Теорема 1. Перестановка f является четной тогда и только тогда когда и в ее циклическом разложении число циклов четной длины четно.

Здесь под длиною цикла понимается число элементов перестановки, входящих в данный цикл.

На основе этой теоремы алгоритм определения четности перестановки может быть реализован по схеме процедуры O1 с изменениями некоторых действий внутри цикла while.

Function ч1 (var f: TPE): boolean;

var i,j,k:1..n: a: array [1..n] of boolean;

s: boolean;

begin

for i:=1 to n do a[i]:=true; s:=true;

for i:=1 to n do

if a[i] then

begin j:=f[i];

while j<>i do

begin s:= not s; a[j]:=false; j:=f[j] end

end;

ч1:=s

end;

Для доказательства корректности приведенного алгоритма необходимо доказать теорему 1. Для этого подробнее рассмотрим некоторые свойства разложений на циклы и введем дополнительные обозначения.

Пусть перестановка f содержит k циклов следующего вида:

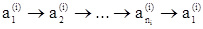, для i=1,...,k,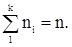

Каждому такому циклу соответствует перестановка f_i = [ 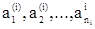], называемая также циклом длины n_i, которая определяется следующим образом:

f_i(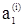)= 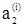,...,f_i(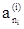)= 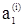; f_i(x)=x для xÏ{ }.

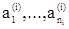Перестановку f можно представить в виде суперпозиции циклов

f = .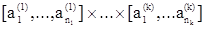

Например, f = <7 5 1 4 2 3 6>, тогда f = [1,7,6,3]×[2,5]×[4].

Замечание. 1. Элементы внутри одного цикла можно циклически переставлять местами.

Например: [1,7,6,3]=[7,6,3,1]=[6,3,1,7]=[3,1,7,6].

2. Представление f в виде суперпозиции коммутативно.

Определение. Перестановку, являющуюся циклом длины 2, будем называть транспозицией.

В дальнейших рассуждениях важную роль будут играть транспозиции соседних элементов, т. е. транспозиции вида [i,i+1], 1£i<n.

Упражнение. Докажите, что если f - транспозиция, то f=f^-1.

Перейдем к доказательству теоремы 1.

Лемма. Перестановку f=<a₁... a_n> можно представить в виде суперпозиции J(f) транспозиций соседних элементов.

Доказательство. Если t=[i,i+1], 1£i<n, то f×t=<a₁ ... a_i-1a_i+1a_ia_i+2...a_n>. пусть t_i - число элементов в f, с которыми i образует инверсию, и расположенных передним. Тогда для того чтобы элемент 1 поставить на первое место, необходимо выполнить t₁ транспозиций соседних элементов; после этого для того чтобы элемент 2 поставить на второе место, необходимо выполнить t₂ транспозиций соседних элементов, и т. д. Таким образом, после t₁+...+t_т=J(f) шагов получим единичную перестановку - e, т. е. f×t₁×...×t_J(f)=e, где t₁,...,t_J(f) -транспозиции соседних элементов.

Итак, f=(t₁×¼×t_J(f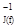))^-1=t ×¼×t 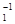, что завершает доказательство леммы, так как t^-1=t для произвольной транспозиции t.

Лемма 2. Для произвольных перестановок f,gÎS_n

sgn(f×g)=sgn(f)×sgn(g).

Доказательство. 1) Пусть g=t=[i,i+1], 1£i<n, f=<a₁... a_n>; тогда f×g=<a₁,...,a_i-1a_i+1a_ia_i+1,...,a_n>

J(f×g)= ,

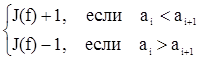т. е. sgn(f×t) = -(-1)^J(f).

2) В случае произвольной перестановки g=t₁×¼×t_k, где t₁,...,t_k - транспозиции соседних элементов и k=J(g), имеем

sgn(f×g)=sgn(f×t₁×¼×t_k)=-sgn(f×t₁×¼×t_k-1)=¼=(-1)^k×sgn(f)=sgn(g)×sgn(f).

Лемма 3. Каждая транспозиция есть нечетная перестановка.

Доказательство. Рассмотрим перестановку

<1... i-1 j i+1...j-1 i j+1...n>.

Ее можно преобразовать в единичную, произведя сначала j-i транспозиций [j-1,j], [j-2,j-1],...,[i,i+1] (i переводится на i-е место); затем (j-i)-1 транспозиций [i+1,i+2],[i+2,i+3],... [i-1,j] (j переводится с i+1-го на j-е место). Это значит, что [i,j] может быть представлена в виде суперпозиции 2×(j-i)-1 транспозиций соседних элементов. По предыдущей лемме sgn([i,j])=(-1)^2×(j-i)-1=-1.

Лемма 4. Знак произвольного цикла длины к равен (-1)^k-1.

Доказательство. Заметим, что [a₁,...a_k]=[a₁,a₂]×[a₁,a₃]×¼×[a₁,a_k].

Доказательство теоремы 1 следует из леммы 4.

Замечание. Будем говорить, что перестановка f есть перестановка типа < 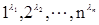>,если она содержит в разложении на циклы в точностиl_i циклов длины i (в случае если l_i=0, то 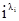обычно опускается). Определение знака перестановки через инверсии может быть дано для множеств, на которых задан линейный порядок. Однако знак перестановки зависит только от ее типа, а не от порядка, определенного на X.