Эквивалентные уравнения

О.И. Садыкова

О.В. Головина

Учебное пособие для слушателей подготовительного отделения по

Алгебре и началам анализа

ОГЛАВЛЕНИЕ

1. Уравнения

1.1. Эквивалентные уравнения

1.2. Рациональные уравнения с одним неизвестным

1.3. Уравнения, содержащие знак абсолютной величины

1.4. Иррациональные уравнения

1.5. Тождественные преобразования показательных
и логарифмических выражений

1.6. Показательные уравнения

1.7. Логарифмические уравнения

1.8. Вопросы и задания для самоподготовки

1.9. Тесты по теме «Уравнения»

1.10. Задачи для самостоятельного решения

2. Литература

Уравнения

Эквивалентные уравнения

Два уравнения

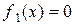и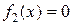

называются равносильными (эквивалентными), если совпадают множества всех их решений или оба они не имеют решений и обозначают .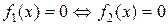

Из определения равносильности уравнения следует, что вместо того, чтобы решать данное уравнение, можно решать уравнение ему равносильное.

Пример

1. Уравнение 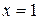равносильно уравнению 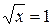, так как число 1 является корнем каждого уравнения, а других корней ни одного из этих уравнений не имеет.

2. 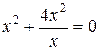и уравнение 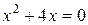, полученное после сокращения дроби 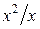, неравносильны. В результате такого преобразования получается значение 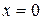, не принадлежащее области допустимых значений (О.Д.З.) данного уравнения.

Уравнение 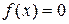считают эквивалентным двум (или нескольким) уравнениям 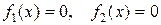, если множество корней уравнения 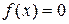совпадает с объединением множеств корней уравнений .

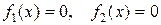Некоторые эквивалентные уравнения:

1) уравнение 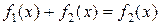эквивалентно уравнению 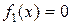, рассматриваемому на множестве допустимых значений исходного уравнения;

2) уравнение 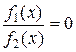эквивалентно уравнению 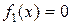, рассматриваемому на множестве значений исходного уравнения;

3) уравнение 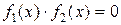эквивалентно двум уравнениям: 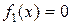и 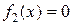, каждое из которых рассматривается на множестве допустимых значений исходного уравнения;

4) уравнение 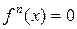эквивалентно уравнению ;

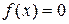5) уравнение 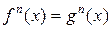при нечетном n эквивалентно уравнению 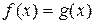, а при четном n эквивалентно двум уравнениям: 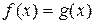и .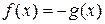

Замечания:

1. От возведения в квадрат обеих частей уравнения нарушается равносильность уравнений, могут появиться посторонние корни. Это особенно важно при решении тригонометрических уравнений, где сложно произвести отборку полученных решений.

2. При проверке корней их значение необходимо подставлять именно в исходное уравнение или в равносильное ему.

3. При делении левой и правой частей уравнения на общий множитель, содержащий неизвестную величину, возможна потеря корней (если этот множитель в О.Д.З. уравнения обращается в нуль). Можно сокращать только в том случае, если он не равен нулю.