Иррациональным уравнением называют уравнение, содержащее неизвестное под знаком корня (радикала). Область допустимых значений иррационального уравнения состоит из тех значений неизвестного, при которых неотрицательны все выражения, стоящие под знаками радикалов четной степени.
Используя О.Д.З. иррационального уравнения, иногда удается решить уравнение, не прибегая к преобразованиям.
Пример 1. Решить уравнение 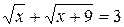 .
.
Решение.О.Д.З. уравнения определяется системой неравенства
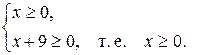
На О.Д.З. уравнения имеем 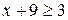 и
и 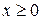 , т. е. его левая часть не меньше 3, а правая равна 3. Исходя из О.Д.З., единственное решение данного уравнения
, т. е. его левая часть не меньше 3, а правая равна 3. Исходя из О.Д.З., единственное решение данного уравнения 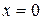 .
.
Ответ: 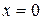 .
.
Один из способов решения иррационального уравнения заключается в последовательном возведении обеих частей уравнения в степень, являющуюся наименьшим общим кратным показателей всех радикалов, входящих в данное уравнение. При этом, если степень, в которую возводится уравнение, четная, то полученное следствие исходного уравнения может иметь посторонние корни. Проверка осуществляется непосредственной подстановкой корней в исходное иррациональное уравнение.
Пример 2. Решить уравнение 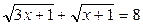 .
.
Решение. Уединим один из корней в левой части:
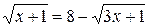 .
.
Возводя в квадрат обе части уравнения, имеем
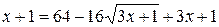 .
.
Приводя подобные члены и уединяя радикал в левую часть, получим
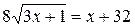 .
.
Возводя обе части в квадрат, имеем
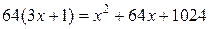 ,
,
т. е. уравнение
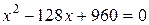 ,
,
корни которого 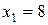 и
и 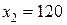 .
.
Подставим каждый из этих корней в исходное уравнение.
При 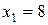 получим верное числовое равенство.
получим верное числовое равенство.
При 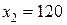 получим
получим 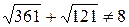 т. е.
т. е. 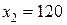 – посторонний корень.
– посторонний корень.
Ответ: 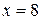 .
.
Уравнения вида
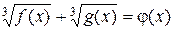 , (1)
, (1)
где 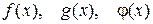 – некоторые функции, обычно решают следующим образом. Возводят обе части уравнения в куб и получают уравнение
– некоторые функции, обычно решают следующим образом. Возводят обе части уравнения в куб и получают уравнение
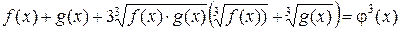 .
.
В этом уравнении заменяют выражение 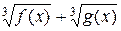 , являющееся левой частью исходного уравнения, на
, являющееся левой частью исходного уравнения, на 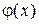 . Затем действуют по обычной схеме.
. Затем действуют по обычной схеме.
Уравнение вида (1) может быть также решено введением вспомогательных неизвестных, что в ряде случаев позволяет перейти от иррационального уравнения к системе рациональных уравнений, являющейся его следствием.
Пример 3. Решить уравнение 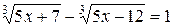 .
.
Решение. Первый способ. Возводя обе части уравнения в куб,
получим
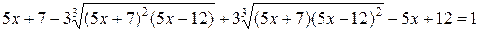 .
.
Приводя подобные члены, получим
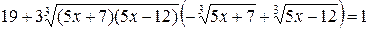 .
.
По условию
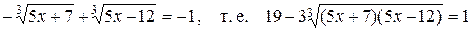 ,
,
или
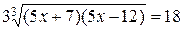 . (2)
. (2)
Возводим уравнение (2) в куб:
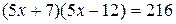 .
.
Последнее уравнение имеет корни 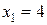 и
и 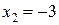 . Проверка показывает, что оба корня удовлетворяют исходному уравнению.
. Проверка показывает, что оба корня удовлетворяют исходному уравнению.
Второй способ. Обозначим 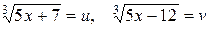 . Исключая
. Исключая 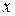 из уравнений
из уравнений 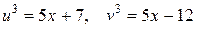 , приводим к системе
, приводим к системе
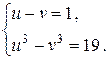
Ее решение сводится к уравнению 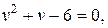 корни которого
корни которого 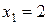 ;
; 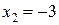 .
.
Возвращаясь к исходному неизвестному, получаем линейные уравнения:
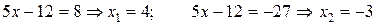 .
.
Проверкой убеждаемся, что корни 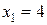 и
и 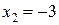 являются корнями исходного уравнения.
являются корнями исходного уравнения.
Ответ: 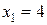 ,
, 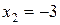 .
.
Пример 4. Решить уравнение 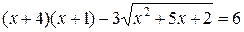 .
.
Решение. Обозначая 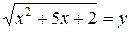 , получим следующую систему уравнений:
, получим следующую систему уравнений:
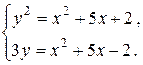 (3)
(3)
Исключая из системы (3) неизвестное 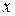 , получаем
, получаем 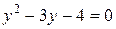 .
.
Корнями этого уравнения являются 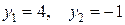 . Так как через
. Так как через 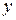 обозначен арифметический корень, то из двух найденных корней уравнения выбираем положительный. Подставляем его во второе уравнение системы (3), получаем для
обозначен арифметический корень, то из двух найденных корней уравнения выбираем положительный. Подставляем его во второе уравнение системы (3), получаем для 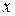 уравнение
уравнение
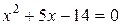 ,
,
корни которого 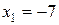 ,
, 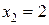 . Делая проверку, убеждаемся, что оба корня являются корнями исходного уравнения.
. Делая проверку, убеждаемся, что оба корня являются корнями исходного уравнения.
Ответ: 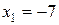 ,
, 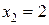 .
.
В некоторых случаях метод выделения полных квадратов в подкоренных выражениях позволяет упростить процедуру решения уравнения.
Пример 5. Решить уравнение
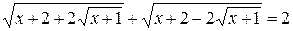 .
.
Решение. Обозначаем 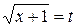 . Тогда исходное уравнение приобретает вид
. Тогда исходное уравнение приобретает вид
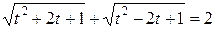 . (4)
. (4)
Так как под радикалами в левой части уравнения (4) стоят полные квадраты, то оно может быть представлено в эквивалентном виде
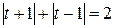 . (5)
. (5)
Данное уравнение эквивалентно следующим уравнениям:
1)  ;
;
2) 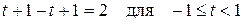 ;
;
3) 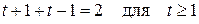 .
.
Первое уравнение не имеет решений; второе уравнение обращается в тождество для всех 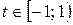 ; третье уравнение имеет решение
; третье уравнение имеет решение 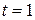 .
.
Возвращаясь к исходному неизвестному, решением имеем 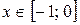 .
.
Ответ: 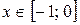 .
.
1.5. Тождественные преобразования показательных
и логарифмических выражений
Пусть 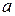 – положительное число, отличное от единицы, а
– положительное число, отличное от единицы, а 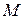 – любое положительное число. Логарифмом числа
– любое положительное число. Логарифмом числа 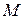 по основанию
по основанию 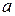 называется такое число, обозначаемое
называется такое число, обозначаемое 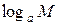 , что соответствует
, что соответствует
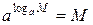 .
.
 2015-01-21
2015-01-21 613
613







