1. Пересечение подпространств является подпространством. Поэтому понятия размерности, базиса и т.п. применяются к пересечениям.
2. Сумма подпространств является подпространством. Поэтому понятия размерности, базиса и т.п. применяются к суммам.
Действительно, нужно показать замкнутость линейных операций в множестве  . Пусть два вектора
. Пусть два вектора  и
и 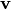 принадлежат сумме
принадлежат сумме 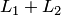 , т.е. каждый из них раскладывается по подпространствам:
, т.е. каждый из них раскладывается по подпространствам:
Найдем сумму:. Так как 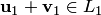 , а
, а 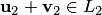 , то
, то 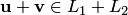 . Следовательно, множество
. Следовательно, множество 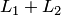 замкнуто по отношению к операции сложения. Найдем произведение:. Так как
замкнуто по отношению к операции сложения. Найдем произведение:. Так как 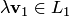 , a
, a 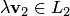 , то
, то 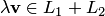 . Следовательно, множество
. Следовательно, множество 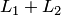 замкнуто по отношению к операции умножения на число. Таким образом,
замкнуто по отношению к операции умножения на число. Таким образом, 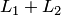 — линейное подпространство.
— линейное подпространство.
3. Операция пересечения определена на множестве всех подпространств линейного пространства 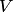 . Она является коммутативной и ассоциативной. Пересечение любого семейства подпространств V является линейным подпространством, причем скобки в выражении
. Она является коммутативной и ассоциативной. Пересечение любого семейства подпространств V является линейным подпространством, причем скобки в выражении 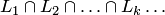 — можно расставлять произвольно или вообще не ставить.
— можно расставлять произвольно или вообще не ставить.
4. Минимальным линейным подпространством, содержащим подмножество 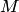 конечномерного линейного пространства
конечномерного линейного пространства 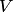 , называется пересечение всех подпространств
, называется пересечение всех подпространств 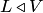 , содержащих
, содержащих 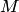 , т.е.
, т.е. 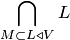 . Если
. Если 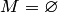 , то указанное пересечение совпадает с нулевым подпространством
, то указанное пересечение совпадает с нулевым подпространством 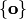 , поскольку оно содержится в любом из подпространств
, поскольку оно содержится в любом из подпространств 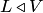 . Если
. Если 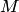 — линейное подпространство
— линейное подпространство 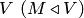 , то указанное пересечение совпадает с
, то указанное пересечение совпадает с 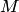 , поскольку
, поскольку 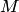 содержится в каждом из пересекаемых подпространств (и является одним из них:
содержится в каждом из пересекаемых подпространств (и является одним из них: 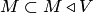 ).
).
|
|
|
Минимальное свойство линейной оболочки: линейная оболочка 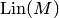 любого подмножества
любого подмножества 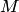 конечномерного линейного пространства
конечномерного линейного пространства 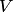 является минимальным линейным подпространством, содержащим
является минимальным линейным подпространством, содержащим 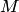 , т.е.
, т.е. 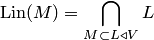 .
.
Действительно, обозначим 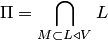 . Надо доказать равенство двух множеств:
. Надо доказать равенство двух множеств: 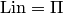 . Так как
. Так как 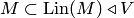 (см. пункт 6 замечаний 8.7), то
(см. пункт 6 замечаний 8.7), то 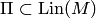 . Докажем включение
. Докажем включение 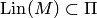 . Произвольный элемент
. Произвольный элемент 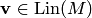 имеет вид
имеет вид 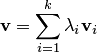 , где
, где 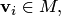
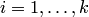 . Пусть
. Пусть 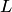 — любое подпространство, содержащее
— любое подпространство, содержащее  . Оно содержит все векторы
. Оно содержит все векторы 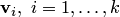 и любую их линейную комбинацию (см. пункт 7 замечаний 8.7), в частности, вектор
и любую их линейную комбинацию (см. пункт 7 замечаний 8.7), в частности, вектор 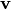 . Поэтому вектор
. Поэтому вектор 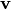 принадлежит любому подпространству
принадлежит любому подпространству 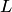 , содержащему
, содержащему 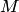 . Значит,
. Значит, 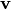 принадлежит пересечению
принадлежит пересечению 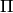 таких подпространств. Таким образом,
таких подпространств. Таким образом, 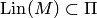 . Из двух включений
. Из двух включений 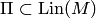 и
и 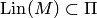 следует равенство
следует равенство 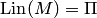 .
.
5. Операция сложения подпространств определена на множестве всех подпространств линейного пространства 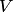 . Она является коммутативной и ассоциативной. Поэтому в суммах
. Она является коммутативной и ассоциативной. Поэтому в суммах 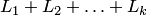 конечного числа подпространств скобки можно расставлять произвольно или вообще не ставить.
конечного числа подпространств скобки можно расставлять произвольно или вообще не ставить.
6. Можно определить объединение 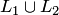 подпространств
подпространств 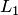 и
и 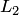 как множество векторов, каждый из которых принадлежит пространству
как множество векторов, каждый из которых принадлежит пространству 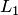 или пространству
или пространству 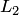 (или обоим подпространствам). Однако, объединение подпространств в общем случае не является подпространством (оно будет подпространством только при дополнительном условии
(или обоим подпространствам). Однако, объединение подпространств в общем случае не является подпространством (оно будет подпространством только при дополнительном условии 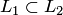 или
или 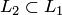 ).
).
|
|
|
7. Сумма подпространств 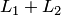 совпадает с линейной оболочкой их объединения
совпадает с линейной оболочкой их объединения 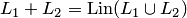 . Действительно, включение
. Действительно, включение 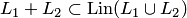 следует из определения. Любой элемент множества
следует из определения. Любой элемент множества 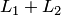 имеет вид
имеет вид 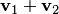 , т.е. представляет собой линейную комбинацию двух векторов из множества
, т.е. представляет собой линейную комбинацию двух векторов из множества 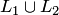 . Докажем противоположное включение
. Докажем противоположное включение 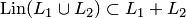 . Любой элемент
. Любой элемент 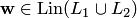 имеет вид
имеет вид 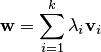 , где
, где 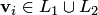 . Разобьем эту сумму на две, относя к первой сумме все слагаемые
. Разобьем эту сумму на две, относя к первой сумме все слагаемые 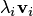 , у которых
, у которых 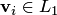 . Остальные слагаемые составят вторую сумму:
. Остальные слагаемые составят вторую сумму:
Первая сумма — это некоторый вектор 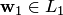 , вторая сумма — это некоторый вектор
, вторая сумма — это некоторый вектор 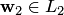 . Следовательно,
. Следовательно, 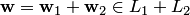 . Значит,
. Значит, 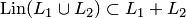 . Полученные два включения говорят о равенстве рассматриваемых множеств.
. Полученные два включения говорят о равенстве рассматриваемых множеств.
Теорема 8.4 о размерности суммы подпространств. Если 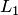 и
и 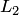 подпространства конечномерного линейного пространства
подпространства конечномерного линейного пространства 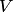 , то размерность суммы подпространств равна сумме их размерностей без размерности их пересечения (формула Грассмана):
, то размерность суммы подпространств равна сумме их размерностей без размерности их пересечения (формула Грассмана):
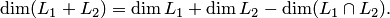
| (8.13) |
В самом деле, пусть 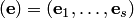 — базис пересечения
— базис пересечения 
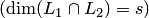 . Дополним его упорядоченным набором
. Дополним его упорядоченным набором 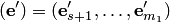 векторов до базиса
векторов до базиса 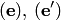 подпространства
подпространства 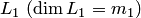 и упорядоченным набором
и упорядоченным набором 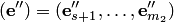 векторов до базиса
векторов до базиса 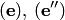 подпространства
подпространства 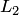
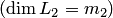 . Такое дополнение возможно по теореме 8.2. Из указанных трех наборов векторов составим упорядоченный набор
. Такое дополнение возможно по теореме 8.2. Из указанных трех наборов векторов составим упорядоченный набор 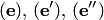 векторов. Покажем, что эти векторы являются образующими пространства
векторов. Покажем, что эти векторы являются образующими пространства 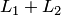 . Действительно, любой вектор
. Действительно, любой вектор 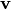 этого пространства представляется в виде линейной комбинации векторов из упорядоченного набора
этого пространства представляется в виде линейной комбинации векторов из упорядоченного набора 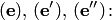
Следовательно, 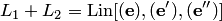 . Докажем, что образующие
. Докажем, что образующие 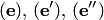 линейно независимы и поэтому они являются базисом пространства
линейно независимы и поэтому они являются базисом пространства 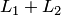 . Действительно, составим линейную комбинацию этих векторов и приравняем ее нулевому вектору:
. Действительно, составим линейную комбинацию этих векторов и приравняем ее нулевому вектору:
| (8.14) |
Первые две суммы обозначим 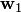 — это некоторый вектор из
— это некоторый вектор из 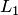 , последнюю сумму обозначим
, последнюю сумму обозначим 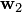 — это некоторый вектор из
— это некоторый вектор из 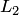 . Равенство (8.14):
. Равенство (8.14): 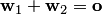 означает, что вектор
означает, что вектор 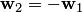 принадлежит также и пространству
принадлежит также и пространству 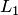 . Значит,
. Значит, 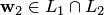 . Раскладывая этот вектор по базису
. Раскладывая этот вектор по базису 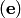 , находим
, находим 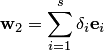 . Учитывая разложение этого вектора в (8.14), получаем
. Учитывая разложение этого вектора в (8.14), получаем
Последнее равенство можно рассматривать, как разложение нулевого вектора по базису 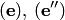 подпространства
подпространства 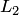 . Все коэффициенты такого разложения нулевые:
. Все коэффициенты такого разложения нулевые: 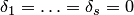 и
и 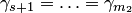 . Подставляя
. Подставляя 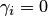 в (8.14), получаем. Это возможно только в тривиальном случае
в (8.14), получаем. Это возможно только в тривиальном случае 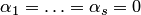 и
и 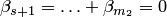 , так как система векторов
, так как система векторов 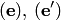 линейно независима (это базис подпространства
линейно независима (это базис подпространства 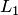 ). Таким образом, равенство (8.14) выполняется только в тривиальном случае, когда все коэффициенты равны нулю одновременно. Следовательно, совокупность векторов
). Таким образом, равенство (8.14) выполняется только в тривиальном случае, когда все коэффициенты равны нулю одновременно. Следовательно, совокупность векторов 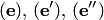 линейно независима, т.е. является базисом пространства
линейно независима, т.е. является базисом пространства 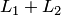 . Подсчитаем размерность суммы подпространств:
. Подсчитаем размерность суммы подпространств:
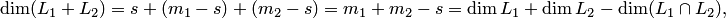
что и требовалось доказать.
Пример 8.6. В пространстве 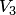 радиус-векторов с общим началом в точке
радиус-векторов с общим началом в точке 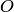 заданы подпространства:
заданы подпространства: 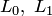 и
и 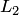 — три множества радиус-векторов, принадлежащих пересекающимся в точке
— три множества радиус-векторов, принадлежащих пересекающимся в точке 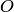 прямым
прямым 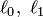 и
и 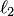 соответственно;
соответственно; 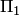 и
и 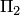 — два множества радиус-векторов, принадлежащих пересекающимся плоскостям
— два множества радиус-векторов, принадлежащих пересекающимся плоскостям 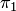 и
и 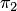 соответственно; прямая
соответственно; прямая 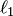 , при надлежит плоскости
, при надлежит плоскости 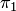 , прямая
, прямая 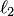 принадлежит плоскости
принадлежит плоскости 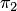 , плоскости
, плоскости 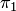 и
и 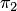 пересекаются по прямой
пересекаются по прямой 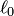 (рис. 8.2). Найти суммы и пересечения каждых двух из указанных пяти подпространств.
(рис. 8.2). Найти суммы и пересечения каждых двух из указанных пяти подпространств.
Решение. Найдем сумму 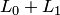 . Складывая два вектора, принадлежащих
. Складывая два вектора, принадлежащих 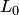 и
и 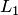 соответственно, получаем вектор, принадлежащий плоскости
соответственно, получаем вектор, принадлежащий плоскости 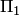 . На оборот, любой вектор
. На оборот, любой вектор 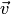 (см. рис.8.2), принадлежащий
(см. рис.8.2), принадлежащий 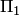 , можно представить в виде
, можно представить в виде 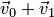 , построив проекции
, построив проекции 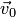 и
и 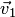 вектора
вектора 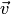 на прямые
на прямые 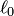 и
и 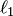 соответственно. Значит, любой радиус-вектор плоскости
соответственно. Значит, любой радиус-вектор плоскости 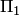 раскладывается по подпространствам
раскладывается по подпространствам 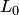 и
и 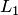 , т.е.
, т.е. 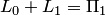 . Аналогично получаем, что
. Аналогично получаем, что 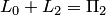 , а
, а 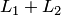 — множество радиус-векторов, принадлежащих плоскости, проходящей через прямые
— множество радиус-векторов, принадлежащих плоскости, проходящей через прямые 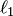 и
и 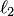 .
.
Найдем сумму 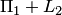 . Любой вектор
. Любой вектор 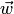 пространства
пространства 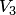 можно разложить по подпространствам
можно разложить по подпространствам 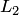 и
и 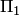 . В самом деле, через конец радиус-вектора
. В самом деле, через конец радиус-вектора 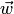 проводим прямую, параллельную прямой
проводим прямую, параллельную прямой 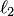 (см. рис. 8.2), т.е. строим проекцию
(см. рис. 8.2), т.е. строим проекцию 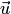 вектора
вектора 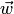 на плоскость
на плоскость  . Затем на
. Затем на  откладываем вектор
откладываем вектор 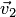 так, чтобы
так, чтобы 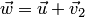 . Следовательно,
. Следовательно, 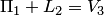 . Так как
. Так как 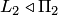 , то
, то 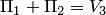 . Аналогично получаем, что
. Аналогично получаем, что 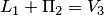 . Остальные суммы находятся просто:
. Остальные суммы находятся просто: 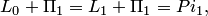
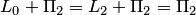 . Заметим, что
. Заметим, что 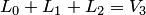 .
.
|
|
|
Используя теорему 8.4, проверим, например, равенство 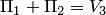 по размерности. Подставляя
по размерности. Подставляя 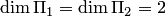 и
и 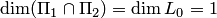 в формулу Грассмана, получаем
в формулу Грассмана, получаем 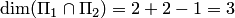 , что и следовало ожидать, так как
, что и следовало ожидать, так как 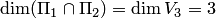 .
.
Пересечения подпространств находим по рис. 8.2, как пересечение геометрических фигур:
где 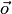 — нулевой радиус-вектор
— нулевой радиус-вектор 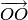 .
.
47. Пряма сума підпросторів. Критерії прямої суми.
 2015-02-27
2015-02-27 6178
6178