Для целей, которые станут ясными из следующих параграфов, представляет интерес деление или «разбиение» состояний автомата на классы по следующим правилам: (1) все состояния, принадлежащие к одному классу, должны быть k-эквивалентными; (2) все состояния, принадлежащие к разным классам, должны быть k-различимыми. Такое разбиение называется k-эквивалентным разбиением автомата и обозначается P k. Классы P k называются классами k-эквивалентности и обозначаются Σk1, Σk2, Σk3 и т. д. Состояния, принадлежащие к одному и тому же классу, называются смежными состояниями; состояния, принадлежащие к разным классам, называются разобщенными состояниями.
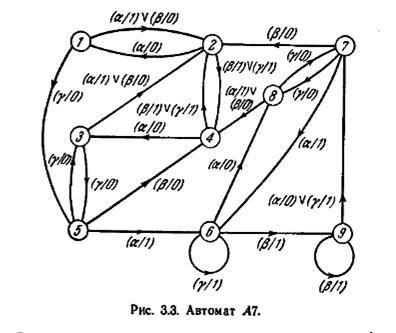
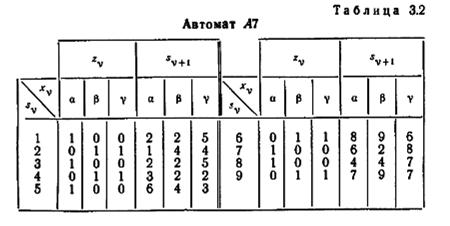
Рис. 3.3 и таблица 3.2 представляют автомат А7, Для этого автомата 2-эквивалентное разбиение имеет вид

Легко проверить по графу переходов автомата А7, что смежные состояния в P2 заданные выражениями (3.1), являются 2-эквивалентными, а разобщенные состояния являются 2-различимыми. Ни одно состояние автомата A7 не является 2-эквивалентным состоянию 9 (за исключением самого состояния 9), и, следовательно, состояние 9 образует класс, состоящий из одного состояния, — одноэлементный класс.
Ясно, что ни одно состояние не может принадлежать одновременно двум различным k-эквивалентным классам, поскольку это означало бы, что это состояние является k-различимым по отношению к самому себе. Следовательно, общее число состояний в Р к равно общему числу состояний в автомате.
Лемма 3.5. k-эквивалентное разбиение автомата единственно.
Доказательство. Предположим, что разбиение Р к, состоящее из Σk1, Σk2,..., Σku, не является единственным. Тогда для этого же автомата должно быть другое k-эквивалентное разбиение, скажем Р´ k, состоящее из Σ´k1, Σ´k2, Σ´k3. Пусть Σkr ={σr1, σr2,..., σr d }. Поскольку состояния из Σkr являются k-эквивалентными и поскольку не
имеется ни одного состояния вне Σkr, являющегося эквивалентным какому-либо состоянию из Σkr, то в Рk, должен быть класс состояний, скажем Σ´kr, состоящий из состояний σr1, σr2,..., σr d и не содержащий никаких других состояний. Предположив, что г принимает значения 1,2,..., u, получим, что каждому классу в P k соответствует идентичный класс в Р´ k Поскольку общее число состояний в P k должно быть таким же, как в Р k, то P k и Р´ k должны быть одинаковыми и, следовательно, P k является единственным.
Лемма 3.6. Состояния, являющиеся разобщенными в Р k, должны быть разобщенными в Р k+1.
Доказательство. Согласно лемме 3.4 два состояния, являющиеся k-различимыми, являются и (k+1)-различимыми. Тогда - справедливость доказываемой леммы непосредственно вытекает из определения P k и P k+1.
Например, Р 3 автомата A7 не может содержать такие классы, как {1, 3, 6} и {2, 5, 9}, поскольку эти классы, как следует из (3.1), содержат состояния, которые в Р 2 являются разобщенными.
Лемма 3.7. Если автомат М имеет два различимых, но k-эквивалентных состояния, то он также должен иметь два состояния, которые являются k-эквивалентными, но (k+1)-различимыми.
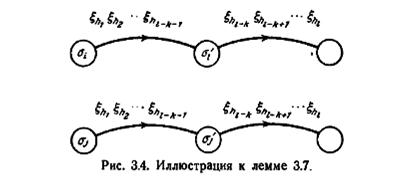
Доказательство. Пусть σ i и σ j будут различимыми k -эквивалентными состояниями автомата М и пусть входная Последовательность ξh 1, ξh 2;..., ξh i будет наикратчайшей входной последовательностью, различающей состояния σ i и σ j. Это значит, что σ i и σ j вырабатывают различные выходные символы не раньше, чем будет приложен входной символ ξh i. Поскольку σ i = σ j являются k-эквивалентными, то должно быть i > k. Пусть (i — k — 1)-ми преемниками σ i = σ j по отношению к входной последовательности ξh 1, ξh 2;..., ξh( i-k-1 ) будут σ´ i и σ´ j, соответственно; так как i > k, то i - k – 1≥0, и эти преемники всегда существуют. Тогда σ´ i и σ´ j могут быть различимы при входной последовательности ξh i-k, ξh i-k+1;..., ξh i, длина которой равна i — (i — k — 1)=k + 1. Эти два состояния не могут быть различимы с помощью никакой другой более короткой последовательности, так как это противоречило бы условию, что σ i и σ j являются k-эквивалентными. Следовательно, σ´ i и σ´ j, являются k-эквивалентными, но (k + 1)-различимыми. Лемма доказана. Рассмотренная ситуация иллюстрируется на рис. 3.4.
Предположим теперь, что смежные состояния в каждом классе эквивалентности разбиения P k являются эквивалентными. Тогда ясно, что Р к+u совпадает с Р к для всех неотрицательных целых и. Если два смежных состояния в P k являются различимыми, то они представляют собой два различимых состояния, которые являются k-эквивалентными. В этом случае, согласно лемме 3.7, автомат должен иметь два состояния, которые являются k-эквивалентными, но (k + 1)-различимыми. Следовательно, Р к должно содержать два смежных состояния, которые становятся разобщенными в P k + i. Таким образом, если смежные состояния в каком-нибудь классе из Р k являются различимыми, то разбиение P k + i должно отличаться от разбиения Р k. Если Р k отличается от Р k, то, согласно лемме 3.6, должно существовать «собственное разделение» Р k, которое должно получаться расщеплением одного или нескольких классов Рк на два или более подклассов. В заключение можно утверждать следующее.
Теорема 3.4. P k+1 должно быть собственным разделением Р k, если не во всех классах Р k смежные состояния являются эквивалентными. В противном случае Р k и P k+1 совпадают.

 2015-02-27
2015-02-27 645
645








