Кратные безусловные диагностические эксперименты

Очевидный недостаток простого эксперимента заключается в том, что он может оказаться разрушительным; действительно, если имеется только один экземпляр автомата, то, вообще говоря, нет способа сознательно восстановить начальное состояние для того, чтобы провести новый эксперимент, когда оказалось, что предыдущий эксперимент неудачен. Таким образом, при проведении простых экспериментов полезная информация, которую дает неудающийся эксперимент, никогда не может быть использована для проведения дальнейших экспериментов, так как в то время, когда информация становится доступной, начальное состояние больше нельзя распознать. Если имеется достаточное число экземпляров данной машины, то можно провести ряд экспериментов, каждый из которых сам по себе недостаточен для того, чтобы решить диагностическую задачу, но в совокупности они дают достаточную информацию для того, чтобы распознать начальное состояние. Например, мы пришли к заключению, что нет простого эксперимента, который решает диагностическую задачу для автомата A21, представленного на рис. 4.10, и множества допустимых начальных состояний {5, 6, 7, 8}. Однако если имеются два экземпляра A21, то решение может быть достигнуто следующим образом. Приложим аа к первому экземпляру A21 и β — ко второму экземпляру. Если реакция первого экземпляра есть 01, то начальное состояние есть 8; если реакция есть 10, то начальное состояние есть 7; если реакция есть 00, то начальное состояние есть либо 5, либо 6. В последнем случае реакция второго экземпляра есть 0, если начальное состояние есть 5, и 1, если начальное состояние — 6. Таким образом, диагностическая задача для A21 и множества допустимых начальных состояний {5, 6, 7, 8} может быть решена кратным экспериментом кратности 2 и длины 3.

В данном месте полезно представить следующую теорему.

Теорема 4.7. В минимальном автомате с n состояниями любое множество r состояний (2 ≤ r ≤n) содержит, по меньшей мере, два состояния, которые являются (n — r + 1)-различимыми.

Доказательство. По лемме 3.9, число состояний в каждом классе P_k минимального автомата с n состояниями не превышает n — k. Следовательно, число состояний в каждом классе Р_n-r+1 не превышает n — (n — r+1) = r — 1. Следовательно, по меньшей мере, два состояния в множестве г состояний должны находиться в двух различпых классах Р_n-r+1 и, следовательно, являются.(n — r+ 1)- различимыми.

Пусть для автомата М и множества допустимых начальных состояний А (М) мощности m G_k является A-группой, состоящей из σ-множеств g_k1, g_k2, g_ku. G₀ состоит из простого σ -множества g₀₁, где g₀₁ = A(M). G_k+1 построено из G_k в соответствии со следующими правилами. Если g_ki имеет мощность r≥2, то оно должно содержать, по меньшей мере, два состояния, скажем, σ_j и σ_i которые являются (n — r + 1)-различимыми. Разобьем g_ki на такие подмножества, что два состояния принадлежат одному и тому же подмножеству тогда и только тогда, когда они дают одинаковые реакции на ε (σ_i, σ_j), т. е. на минимальную диагностическую последовательность для {σ_i, σ_j}. Реакция на ε (σ_i, σ_j) тех состояний, которые принадлежат данному подмножеству, называется характеристической реакцией этого подмножества по отношению ε (σ_i, σ_j). σ-множества G_k+1 являются одноэлементными в G_k и во всех подмножествах, полученных по предыдущему правилу. Если g_ki не является одноэлементным, то оно всегда может быть разбито, по крайней мере, на два подмножества, так как реакции σ_j и σ_i на ε (σ_i, σ_j) являются различными. Таким образом, если только G_k не является простым, то Gk+1 всегда представляет собой собственное разделение G_k. Так как мощность А (М) есть m, то G_m-1 должно быть простым.

Описанный выше процесс может быть показан на структуре, называемой деревом кратного эксперимента, определяемой для М и А (М)[25]. В этом дереве каждая ветвь k-го уровня представляет некоторое g_kl, а начальная ветвь представляет g₀₁. Ветвь, представляющая простое g_ki, является оконечной. Если g_ki не является простым и может быть разбито, скажем, на h подмножеств (способом, описанным в предыдущем абзаце), то ветвь, представляющая это g_kl, расщепляется на h ветвей следующего уровня, который представляет h подмножеств, получающихся в процессе разбиения. Используя эти правила, можно развернуть все дерево путем построения k-ro уровня на основе построенного (k—1)-го уровня. Так как множества g_ki, представленные на k-м уровне, являются σ-множествами G_k, то отсюда следует, что высота дерева не может превышать m—1. К тому же дерево должно давать в точности т оконечных ветвей — по одному на каждое допустимое состояние.

Для наглядности все ветви в дереве сложного эксперимента, за исключением оконечных ветвей, изображаются

в форме двухполюсных блоков, представляющих экземпляры заданного автомата. Каждая ветвь снабжается обозначением представляемого ею g_ki. Если g_ki не является однородным, ветвь также обозначается последовательностью ε (σ_i, σ_j), примененной при разбиении g_ki, и характеристической реакцией g_ki по отношению к диагностической последовательности, соответствующей предыдущей ветви.

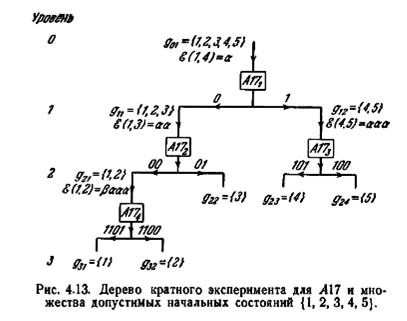
В качестве примера на рис. 4.13 показано дерево кратного эксперимента для автомата А17 (рис. 4.3) и множества допустимых начальных состояний {1, 2, 3, 4, 5}. Начальная ветвь представляет g₀₁={1, 2. 3, 4, 5}, которое есть заданное множество допустимых начальных состояний. Парой состояний { σ_i, σ_j}, использованной для разбиения g_0l, является {1, 4}. В данном случае пара состояний выбрана таким образом, чтобы она дала кратчайшее возможное ε (σ_i, σ_j) (однако это правило выбора в данном методе несущественно). Выбор можно произвести с помощью перечня последовательностей, записанного в таблице 4.6, где ε (1,4), очевидно, есть а. Когда а приложено к A17, подмножество {1, 2, 3} множества g_0l отвечает реакцией 0, а подмножество {4, 5}—реакцией 1, что легко может быть выведено из таблицы переходов или диаграммы для A17. Поэтому начальная ветвь расщепляется на две ветви: ветвь, обозначенную 0, что является характеристической реакцией g₁₁={1. 2, 3} по отношению к ε (1, 4) = а, и ветвь, обозначенную 1, что является характеристической реакцией g₁₂= {4, 5} по отношению к ε (1, 4) = а. Теперь из g₁₁ выбирается пара состояний {1, 3} таким же образом, как {1, 4} была выбрана из g_0l. Когда к A17 приложено ε (1, 3) = aa, подмножество {1, 2} из g₁₁ отвечает реакцией 00, а подмножество {3} из g₁₁ отвечает реакцией 01. Поэтому ветвь, представляющая g₁₁, расщепляется на две ветви: ветвь, обозначенную 00, что является характеристической реакцией g₂₁={l, 2} по отношению к ε (1, 3) = aa, и ветвь, обозначенную 01, что является характеристической реакцией g₂₂={3} на ε (1, 3) = aa. Последняя ветвь является оконечной, так как g₂₂ является одноэлементным множеством. Остаток дерева развертывается аналогичным образом.

Как только дерево кратного эксперимента для М и А(М) построено, кратный эксперимент может быть проведен путем рассмотрения каждого блока на дереве как отдельного экземпляра М и приложения к каждому экземпляру особой диагностической последовательности, связанной с соответствующим блоком. Из правил, сформулированных для построения дерева, следует, что если наблюдаемая реакция всех экземпляров М, которые расположены вдоль некоторого пути по дереву, удовлетворяет перечисленным реакциям для этого пути, то начальное состояние М есть состояние, представленное конечной ветвью пути. Тогда начальное состояние может быть просто распознано путем сравнения действительных реакций экземпляров с реакциями, обозначенными вдоль m различных путей.

Для A17 и его множества допустимых начальных состояний {1, 2, 3, 4, 5} используются четыре экземпляра. Эти экземпляры, обозначенные A17₁, A17₂, A17₃, A17₄, подвергаются воздействию диагностических последовательностей а, аа, ааа и β aaa соответственно, как предписывается деревом сложного эксперимента на рис. 4.13. Если теперь оказывается, что начальное состояние A17 есть 2, то A17₄ должен дать 0, A17₂ должен дать 00 и A17₄ должен дать 1100. Так как эти реакции удовлетворяют реакциям, указанным вдоль пути по дереву, оканчивающегося в g₃₂={2}, начальное состояние распознается как 2.

Очевидно, что действие экземпляра М, связанного с множеством g_ki, состоит в том, чтобы «расщепить» это множество на два или более подмножеств. Так как число расщепляющих операций, требуемых для того, чтобы разделить А(М) на m одноэлементных подмножеств, не превышает m—1, число экземпляров, включенных в дерево кратного эксперимента, не превышает m — 1. Так как длина диагностической последовательности для пары состояний в машине с n состояниями не может превосходить n — 1, общая длина всех последовательностей, включенных в дерево, не может превышать (n—1) (m—1). Таким образом, мы имеем следующую теорему.

Теорема 4.8. Диагностическая задача для автомата с n состояниями и m допустимыми состояниями может всегда быть решена с помощью кратного безусловного эксперимента длины l и кратности с, где

l ≤ (n-1)(m-1) (4.7)

с≤ m-1. (4.8)

Граница в (4.7) существенно выше, чем величина l, встречавшаяся в большинстве задач (хотя она может быть достигнута для m=2), так как, по теореме 4.7, только часть примененных последовательностей должна быть длины n—1. Однако граница в (4.8) может быть достигнута при каждом n и m≤n, как показано на примере автомата A22 с n состояниями (таблица 4.9).

Так как каждый входной символ переводит все состояния A22 в состояние 1, все диагностические последовательности ограничиваются одним символом. Так как каждый входной

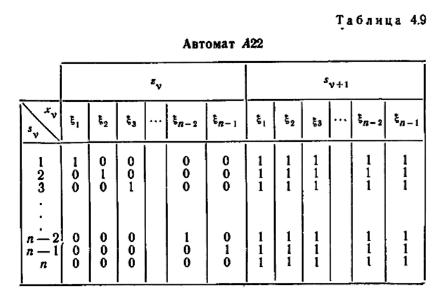
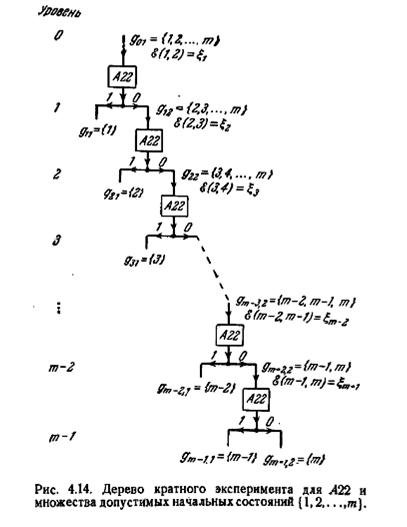
символ способен выполнить в точности одну операцию «расщепления» множества допустимых начальных состояний (независимо от мощности этого множества), диагностический эксперимент для т состояний для A22 требует в точности m—1 экземпляров. Дерево кратного эксперимента для A22 и множества допустимых начальных состояний {1, 2,..., m} показано на рис. 4.14.

Можно отметить, что, хотя метод построения кратного эксперимента может минимизировать длину входной последовательности, прикладываемой к каждому экземпляру, он, вообще говоря, не минимизирует общую длину эксперимента или его кратность. Во многих случаях как длина, так и кратность эксперимента могут быть сокращены посредством использования следующего очевидного факта. Если даны две входные последовательности ε₁ и ε₁ε₂ то реакция автомата М на ε₁ может быть определена по реакции М на ε₁ε₂. Таким образом, если как ε₁, так и ε₁ε₂ являются диагностическими последовательностями, которые должны применяться в кратном эксперименте, то в действительности должна применяться только ε₁ε₂. Например, в кратном эксперименте, описанном на рис. 4.13, реакции A17₁ на а и A17₂ на аа могут быть определены по реакции A17₃ на ааа; следовательно, для эксперимента в действительности требуется только два экземпляра A17. Как легко можно установить, диагностическая задача для A17 и множества допустимых

начальных состояний {1. 2, 3, 4, 5} не может быть решена простым экспериментом, и, следовательно, приведенное выше упрощение обеспечивает достижение наименьшей возможной кратности для этой задачи.