Распознавание сильносвязных (n, р, q)-автоматов

Частичное знание внутренней структуры заданного автомата во многих случаях позволяет выявить его входной и выходной алфавиты и число его состояний. Например, если автомат представляет собой вычислительный прибор, то эта информация может быть получена из знания входного устройства, выходного устройства и числа элементов памяти

прибора. Если число входных символов равно р, число выходных символов—q, а число состояний — q, то эта информация равносильна утверждению, что заданный автомат является (n, р, q)-автоматом. Если, кроме того, известно, что автомат сильносвязный, то можно утверждать, что заданный автомат является сильносвязным (n, р,q)-автоматом.

Класс сильносвязных (n, р, q)-автоматов такой, что никакие два автомата из этого класса не являются эквивалентными, будем обозначать через C_n,p,q. Очевидно, что C_n,p,q является подклассом класса минимальных (n, р, q)-автоматов таких, что никакие два автомата из этого класса не эквивалентны друг другу. Согласно теореме 3.7, последний класс является конечным и, следовательно, C_n,p,q должен быть также конечным. Используя выражение (3.21), находим, что мощность класса C_n,p,q, обозначаемая | C_n,p,q |, определяется выражением

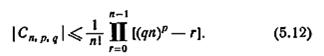
Поскольку, согласно теореме 5.6, C_n,p,q представляет собой исключительный класс, любой его член может быть определен простым безусловным экспериментом длины l, где, по следствию 5.1,

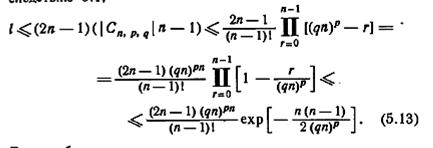
Таким образом имеем:

Теорема 5.10. Если известно, что автомат М является сильносвязным (n, р, q)-автоматом, то М всегда может быть распознан простим безусловным ¦экспериментом длины l, где

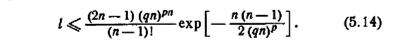
Например, сильносвязный (2, 2, 2)-автомат может быть распознан простым безусловным экспериментом, длина которого не будет превышать 725 символов.

5.8. Автоматы без потери информации [31]

В главе 4 и предыдущих параграфах настоящей главы мы изучали вопросы распознавания неизвестных состояний и неизвестных автоматов. В этом параграфе мы рассмотрим задачу распознавания другого типа — задачу распознавания неизвестной входной последовательности, приложенной к заданному конечному автомату. В частности, эта задача состоит в следующем: неизвестная конечная входная последовательность ε прикладывается к автомату М, таблица переходов которого и начальное состояние σ_i (т. е. состояние

перед приложением входной последовательности ε) известны, а реакция на входную последовательность ε может наблюдаться; построить эксперимент, который, будучи проведенным над автоматом М, после приложений последовательности ε распознает эту последовательность. Автоматы, для которых эта задача может быть решена независимо от ε и σ_i, называются автоматами без потери информации. Автоматы без потери информации в отличие от всех других конечных автоматов, в которых при известных начальном состоянии и приложенной входной последовательности всегда можно определить выходную последовательность, имеют дополнительное свойство: при заданном начальном состоянии по выходной последовательности можно всегда определить входную последовательность.

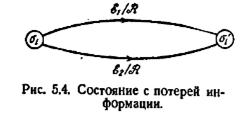
Будем говорить, что состояние σ_i автомата М ведет в состояние σ´_i через ε/Ȓ, если приложение входной последовательности ε к M|σ_i дает выходную последовательность Ȓ и переводит автомат М в состояние σ´_i. Состояние σ_i будем называть состоянием с потерей[32], если оно ведет в некоторое состояние σ´_i через ε₁/ Ȓ и через ε₂/ Ȓ, где ε₁ и ε₂ — две различные входные последовательности. Последнее определение иллюстрируется рис. 5.4

Теорема 5.11. Для того чтобы автомат М был автоматом без потери информации, необходимо и достаточно, чтобы этот автомат не имел состояний с потерей.

Доказательство. Предположим, что автомат М содержит состояние с потерей σ_i такое, как показано на рис. 5.4. Так как выходные последовательности M|σ_i при ε₁ и при ε₂ одинаковы и так как обе последовательности переводят М в одно и то же конечное состояние, то не существует последующего эксперимента, который бы выявил, вызвана выходная последовательность М входной

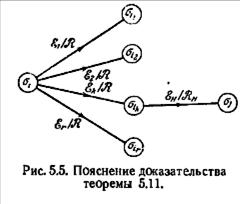
последовательностью ε₁ или ε₂. Таким образом, необходимость условия теоремы очевидна. Предположим теперь, что М не содержит состояний с потерей и что Ȓ наблюдается при приложении неизвестной входной последовательности ε к автомату М в известном начальном состоянии σ_i. По таблице переходов определим все различные входные последовательности, скажем ε₁ε₂...ε_r которым точно соответствует Ȓ; одной из этих последовательностей должна быть ε. Обозначим состояния, в которые ведет σ_i через ε₁/ Ȓ, ε₂/ Ȓ,..., ε_r/ Ȓ, σ_i1, σ_i1,..., σ_ir соответственно. Поскольку, согласно допущению, σ_i не является состоянием с потерей, σ_i1, σ_i1,..., σ_ir должны быть различными и, следовательно, должно существовать взаимно однозначное соответствие между состояниями σ_i и входными последовательностями ε_k. Теперь приложим установочную последовательность, скажем ε _H, построенную для М с множеством допустимых начальных состояний { σ_i1, σ_i1,..., σ_ir }. Обозначим конечное состояние, в которое перейдет автомат после приложения ε _H через σ_i, а выходную последовательность, которая получится при этом, через Ȓ _H. Пара последовательностей вход-выход ε _H /Ȓ _H может относиться только к одному из состояний σ_i1, σ_i1,..., σ_ir по следующим соображениям: допустим, что ε₁ε _H / ȒȒ _H относится к двум состояниям, скажем σ_i1 и σ_i2; тогда σ _i ведет в σ _j через ε₁ε _H / ȒȒ _H и через ε₂ε _H / ȒȒ _H. Однако, так как ε₁, и ε₂ — различные последовательности, это означало бы, что σ_i является состоянием с потерей, что противоречит предположению, по которому автомат М не содержит состояний с потерей. Следовательно, ε _H /Ȓ _H однозначно определяет состояние, в которое автомат переходит из σ_i при приложении ε, и, значит, однозначно определяет ε. Это положение иллюстрируется рис. 5.5, где предполагается, что ε_k является действительной входной последовательностью ε.

Пусть S_j(σ_u) обозначает множество состояний, в которое переходит автомат М из состояния σ_u с выходным символом ζ_j. Если М является автоматом без потери информации, имеющим р входных и q выходных символов, то множества S₁(σ_u), S₂(σ_u) S_q(σ_u) должны содержать полное число элементов р. Теперь пусть «множество D_k(σ_i)» обозначает

некоторое множество состояний, скажем {σ_i1, σ_i2,..., σ_ir}, достижимых из состояния σ_i с выдачей одной и той же выходной последовательности длины k. Тогда множество S_j(σ_i1)US_j(σ_i2)U...US_j(σ_ir) является множеством D_k+l(σ_i). Если М—автомат без потери информации, то число элементов множества D_k+l (σ_i) должно равняться числу всех элементов в множествах S_j(σ_i1),S_j(σ_i2),...,S_j(σ_ir) для любого j. Таким образом, составляя рекурсивно все множества D_k(σ_i) для всех k и i, можно определить, является автомат М автоматом без потери информации или нет.

Указанный критерий может быть легко применен при построении так называемой таблицы проверки В этой таблице каждому столбцу соответствует свой, отличный от других, выходной символ ζ_j. Таблица делится на следующие друг за другом подтаблицы, первая из которых содержит в основном столбце состояния σ₁, σ₂,..., σ_n автомата М, а содержимым клетки, находящейся на пересечении строки σ_u и столбца ζ_j, имеет множество S_j(σ_u). Клетки основного столбца (k+1)-й подтаблицы заполняются содержимым клеток k-й подтаблицы, притом таким, которое не встречалось в основных столбцах предшествующих подтаблиц. В клетке на пересечении строки (σ_i1, σ_i2,..., σ_ir) и столбца ζ_j в (k+1)-й подтаблиие записывается множество S_j(σ_i1)US_j(σ_i2)U...US_j(σ_ir) которое может быть составлено по данным первой подтаблицы. Построение таблицы заканчивается при выполнении одного из следующих условий: (1) число элементов некоторого множества S_j(σ_u) (в первой подтаблице) меньше мощности входного алфавита; (2) число элементов некоторого множества S_j(σ_i1)US_j(σ_i2)U...US_j(σ_ir) (в k-й подтаблице, где k > 1) меньше общего числа элементов множеств S_j(σ_i1),S_j(σ_i2),...,S_j(σ_ir); (3) нельзя добавить ни одной новой строки

в основном столбце. Если условия (1) и (2) не имеют места, то М является автоматом без потери информации. Очевидно, что общее число строк в таблице проверки потерь не может превышать

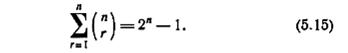
Поэтому проверка потерь информации является конечным процессом.

В качестве примера в таблице 5.9 приведена таблица проверки потерь для автомата A25, заданного графом переходов рис. 5.6 и таблицей 5.8. Первая подтаблица строится

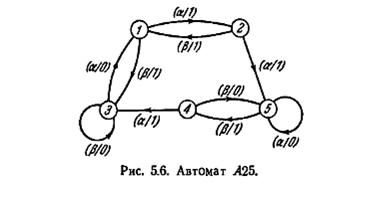
на основании таблицы 5.8. В основной столбец второй подтаблицы переписываются из первой таблицы множества {1, 3}, {1, 5} и {2, 3}, не содержащиеся в основном столбце последней. В клетке второй подтаблицы на пересечении строки {1,5} и столбца 1, например, проставляется набор состояний, стоящих в клетках первой подтаблицы на пересечении строк 1 и 5 и столбца 1, а именно {2, 3, 4}. Остальные клетки таблицы заполняются аналогично. Так как из рассмотрения таблицы 5.9 следует, что условия (1) и (1) не имеют места, автомат А25 является автоматом без потери информации.

Проиллюстрируем, как могут быть определены входные последовательности автомата без потери информации. Пусть известно, что автомат А25 до приложения неизвестной входной последовательности находился в состоянии 1, а в результате приложения этой последовательности выдал выходную

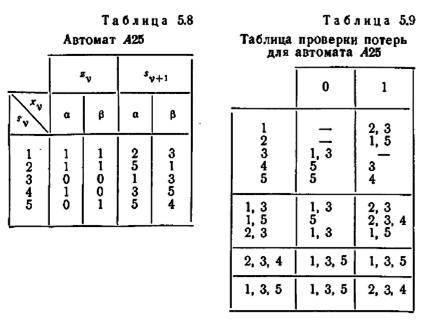
последовательность 111. Из графа переходов, изображенного на рис. 5.6, можно заключить, что последовательность 111 может соответствовать входным последовательностям a β a, а ββ и аа β, которые переводят автомат из состояния 1 в состояния 2, 3 и 4 соответственно. Последовательность а β является установочной последовательностью для автомата А25 с множеством допустимых состояний {2, 3, 4}. При приложении последовательности а β в состояниях 2, 3 и 4 выходные последовательности будут соответственно 11, 01 и 10. Следовательно, истинной входной последовательностью будет а β а, а ββ и аа β, в зависимости от того, какая будет реакция автомата на последовательность а β (приложенную после неизвестной входной последовательности)— 11, 01 или 10 соответственно.

Автомат М без потери информации можно рассматривать как канал связи, в котором сообщение, переданное на входном конце, принято в закодированной форме на выходном конце. Задача декодирования получаемого сообщения может быть успешно разрешена, если получатель знает состояние канала перед передачей каждого сообщения и если канал может быть переведен в известное конечное состояние после

передачи каждого сообщения. Если получатель не может контролировать передающий конец (как это часто имеет место), то второе требование может быть удовлетворено, если отправитель «согласится» заканчивать каждое сообщение последовательностью ε _H, т. е. заранее определенной установочной последовательностью для автомата М и для множества допустимых начальных состояний содержащего все состояния автомата. Например, для автомата А25 и для множества допустимых состояний {1, 2, 3, 4, 5} установочной последовательностью будет ааа. Если отправитель систематически заканчивает каждое сообщение передачей последовательности ааа (или передает ааа в течение определенных, заранее оговоренных интервалов времени), то все переданные сообщения могут быть расшифрованы на приемном конце без необходимости доступа к входным зажимам автомата. Можно также показать, что если отправитель согласен передавать последовательность ε _H и перед каждым сообщением, то принимающему не нужно знать начальное состояние М (т. е. состояние М, в котором к М был приложен первый символ сообщения), так как это начальное состояние может быть определено по реакции автомата на ε _H. Таким образом, если до и после каждого сообщения передается последовательность ε _H, то это сообщение может быть расшифровано с помощью только таблицы переходов М. В нашем случае это означает, что передача каждого сообщения должна начинаться и заканчиваться передачей входной последовательности

Задачи

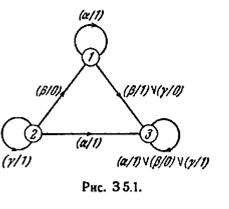
5.1. Постройте автомат, от которого никаким экспериментом длины 4 нельзя отличить автомат, изображенный на Рис. 3 5.1. рис. 3 5.1, но который не эквивалентен этому автомату.

5.2. Известно, что минимальный автомат М имеет два состояния, входной алфавит { а, β} и выходной алфавит {0, 1}. Известно также, что ни Одно из состояний автомата М на графе переходов не имеет петель. Опишите эксперимент, распознающий этот автомат, если его истинное представление такое, как показано

в таблице 3 5.1, и если его действительное начальное состояние 1 (которое сначала не известно).

5.3. Известно, что автомат, определенный таблицей 35.2, неисправен и что в результате неисправности, по крайней мере, вместо одной из «1» вырабатывается «0». Опишите эксперимент, распознающий повреждение, состоящее в том, что в состоянии 1 вместо «1» иа выходе вырабатывается «0», и если.начальным состоянием автомата является состояние 3 (что сначала не известно).

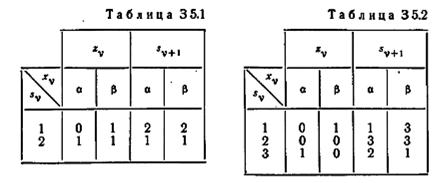
5.4. На рис. 3 5.2 показан неполный граф переходов автомата с двумя состояниями. Опишите эксперимент над автоматом, с помощью которого можно закончить построение графа переходов. Предположите, что искомая дуга обозначается (а /1) и ведет в состояние 1 и что начальным состоянием автомата является состояние 1 (которое сначала не известно).

5.5. Покажите, что автомат М с множеством состояний S = {σ₁, σ₂,..., σ_n} является сильносвязным тогда и только тогда, G(σ_i) = S для i=1, 2,..., n. [Определение G (σ_i) дано в § 2.6.]

5.6. Покажите, что для того, чтобы автомат M c n состояниями был сильиосвязиым, необходимо и достаточно, чтобы матрица 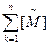не имела нулевых элементов.

5.7. Автоматы M₁ и М₂ являются сильиосвязными и состояние σ_i- автомата М₁ эквивалентно состоянию σ_j автомата М₂. Покажите, что М₁ = М₂.

5.8. Постройте автомат с n состояниями, который является сильиосвязным, ио не содержит ни одного полного контура.

5.9. Автомат М имеет множество состояний S= {σ₁, σ₂,..., σ_n}. Покажите, что: (а) М является обратимым, если в каждом изолированном подавтомате автомата М имеется состояние σ_i такое, что

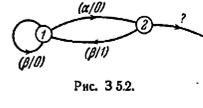
G (σ_i) = F(σ_i); (б) М является сильиосвязиым, если ои имеет состояние σ_i такое, что G(σ_i) = F (σ_i) = S. [Определение G (σ_i) дано в § 2.6; определение F (σ_i) дано в задаче 2.10.]

5.10. Покажите, что если автомат М является сильиосвязиым, то М(с волной) также является сильиосвязиым, что и обратное утверждение не обязательно справедливо.

5.11. Докажите следующее неравенство, использованное в выражении (5.13):

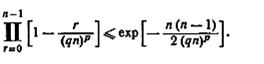
5.12. Известно, что автомат М является сильиосвязиым (n, 2, 2)-автоматом. Покажите, что М всегда может быть распознан простым безусловным экспериментом, длины l, где

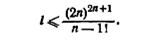
Вычислите верхнее значение l при n = 5.

5.13. Известно, что автомат М является (n, р, q)-автоматом и содержит полный контур. Найдите, верхнее значение длины распознающего М эксперимента (можно предположить, что n≥1).

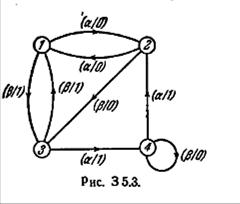
5.14. Определите, является ли автомат A17, изображенный на рис. 3 5.3, автоматом без потери информации.

5.15. Покажите, что автомат, представленный на рис. 3 5.3, является автоматом без потери информации, и опишите распознавание входной последовательности садр, приложенной к этому автомату в состоянии 2.

5.16. Покажите, что автомат является сильиосвязиым, если он имеет любое из следующих свойств: (а) ни в одной строке подтаблицы z _v не содержится двух одинаковых выходных символов; (б) ни в одном столбце матрицы переходов ие имеется двух или более пар вход-выход с одинаковыми выходными символами,