Алгебра логики, как и обычная алгебра, имеет ряд законов, позволяющих переходить от одной формы записи к другой. Для алгебры логики справедливы коммутативные (переместительные), ассоциативные (сочетательные) и дистрибутивные (распределительные) законы обычной алгебры. В приложении к алгебре логики эти законы принимают следующий вид:
Переместительный закон:
а) 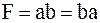 , ,
| (3.13) |
б) 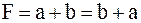 . .
| (3.14) |
Этот закон, как и в обычной алгебре, утверждает, что от перемены мест слагаемых (сомножителей) результат не меняется.
Сочетательный закон:
а) 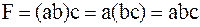 , ,
| (3.15) |
б) 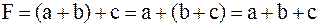 . .
| (3.16) |
При записи конъюнкции и дизъюнкции скобки можно опустить.
Распределительные законы:
а) закон конъюнкции относительно дизъюнкции (закон умножения относительно сложения):
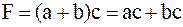 , ,
| (3.17) |
что доказывается раскрытием скобок.
Существует еще один распределительный закон, которого нет в обычной алгебре:
б) закон дизъюнкции относительно конъюнкции (закон сложения относительно умножения):
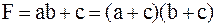 . .
| (3.18) |
Справедливость этого закона можно доказать с помощью эквивалентной релейно-контактной схемы. Для этого построим таблицу состояний для левой и правой частей равенства (таблица 3.6).
|
|
|
Таблица 3.6
| a | b | c | ab | ab+с | a+c | b+c | (a+c)·(b+a) |
Законы нулевого множества:
а) 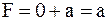 ; ;
| (3.19) |
б) 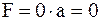 . .
| (3.20) |
Если какая-либо переменная имеет значение 0, независимо от значений других переменных, то их конъюнкция обращается в ноль.
Законы универсального множества:
а) 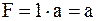 ; ;
| (3.21) |
б) 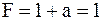 . .
| (3.22) |
Последний закон выполняется только в алгебре логики.
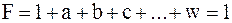 , ,
| (3.23) |
то есть дизъюнкция любого числа переменных обращается в единицу, если хотя бы одна из переменных имеет значение единицы, независимо от значений других переменных.
Только в алгебре логики применяются следующие законы:
Закон повторения:
а) 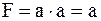 ; ; 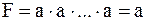 ; ;
| (3.24) |
б) 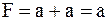 ; ; 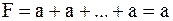 . .
| (3.25) |
Закон дополнительности:
а) 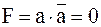 . .
| (3.26) |
Конъюнкция любой переменной и ее инверсии равна нулю.
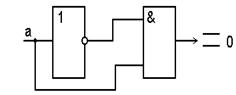
б) 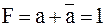 . .
| (3.27) |
Дизъюнкция любой переменной и ее инверсии равна единице.
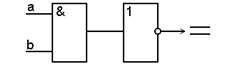
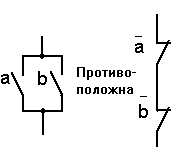
Законы инверсии (законы де Моргана):
а) 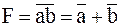 . .
| (3.28) |
Инверсия конъюнкции равна дизъюнкции инверсий (инверсия произведения равна сумме инверсий сомножителей).
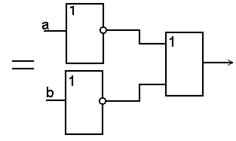
б) 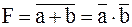 . .
| (3.29) |
Инверсия дизъюнкции равна конъюнкции инверсий (инверсия суммы равна произведению инверсий слагаемых).
Эти законы справедливы для любого числа переменных.
Особую группу составляют законы поглощения, являющиеся выводами из предыдущих законов:
|
|
|
а) 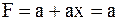 , ,
| (3.30) |
так как 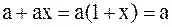 .
.
б) 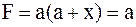 , ,
| (3.31) |
так как 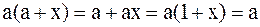 .
.
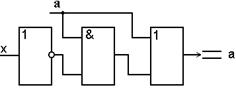
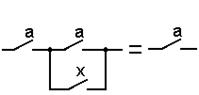
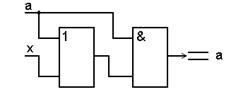
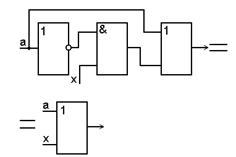
в) 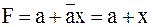 , ,
| (3.32) |
так как если a = 0, то выход определяется состоянием x, а еслиa = 1, то выход равен 1, независимо от состояния x;
г) 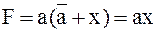 , ,
| (3.33) |
так как
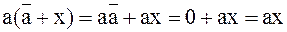 .
.
д) 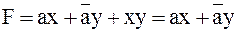 , ,
| (3.34) |
так как
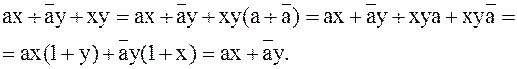
Доказательство этого и других законов алгебры логики легко проследить по релейно-контактному эквиваленту (табл. 3.7).
Таблица 3.7 – Cхемная реализация законов алгебры логики
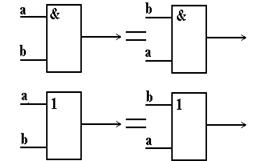
| Закон | Реализация закона с помощью релейно-контактной схемы | Реализация закона с помощью бесконтактных схем |
| 1 Переместительный (коммутативный) аb = bа a + b = b + a | 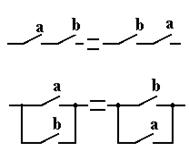
| 
|
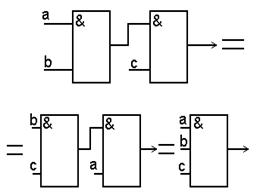
| 2 Сочетательный (ассоциативный) (ab)c = a(bc) | 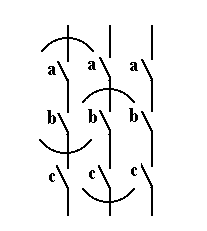
| 
|
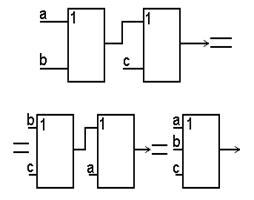
| (a + b) + c = = a + (b + c) | 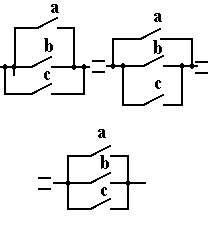
| 
|
Продолжение таблицы 3.7
| Закон | Реализация закона с помощью релейно-контактной схемы | Реализация закона с помощью бесконтактных схем |
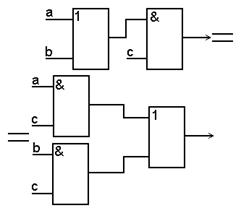
| 3. Распределительный (дистрибутивный) (a + b)c = = ac + bc ab + c = = (a + c)(b + c) | 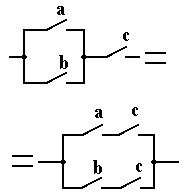
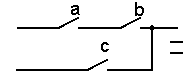
| 
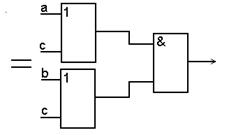
|
| 4 Законы нулевого множества 0 a = 0 0 + a = 0 | 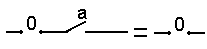
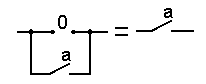
|
Продолжение таблицы 3.7
| Закон | Реализация закона с помощью релейно-контактной схемы | Реализация закона с помощью бесконтактных схем |
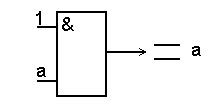
| 5 Законы универсального множества 1 a = a |
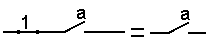
| 
|
| 1 + a = 1 | 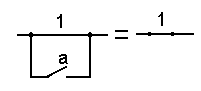
| 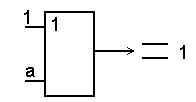
|
| 6 Законы повторения aa...a = a | 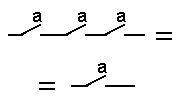
| 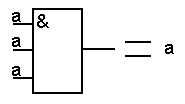
|
| a + a...+ a = a | 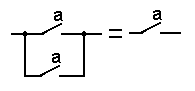
| 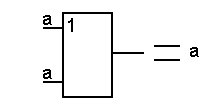
|
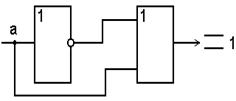
7 Законы дополнительности
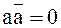
| 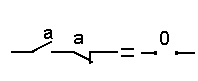
| 
|
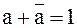
| 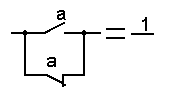
| 
|
Продолжение таблицы 3.7
| Закон | Реализация закона с помощью релейно-контактной схемы | Реализация закона с помощью бесконтактных схем |
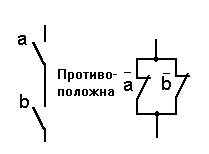
8 Законы
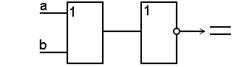
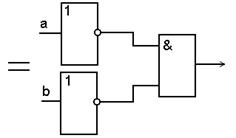
инверсии (правила де Моргана)
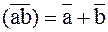
| 
|  
|
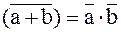
| 
|  
|
9 Законы поглощения
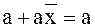
| 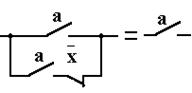
| 
|
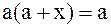
| 
| 
|
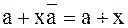
|
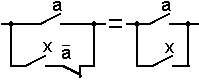
|
|
Продолжение таблицы 3.7
| Закон | Реализация закона с помощью релейно-контактной схемы | Реализация закона с помощью бесконтактных схем |
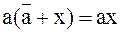
| 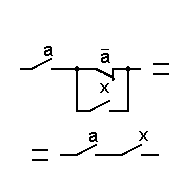
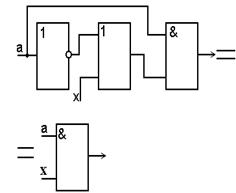
| 
|
 2015-02-27
2015-02-27 656
656








