Общие сведения. Основываясь на модели свободных электронов, можно объяснить ряд важных физических свойств металлов

Основываясь на модели свободных электронов, можно объяснить ряд важных физических свойств металлов. Согласно этой модели, наиболее слабосвязанные (валентные) электроны составляющих металл атомов могут довольно свободно перемещаться в объеме кристаллической решетки. Эти валентные электроны становятся носителями электрического тока в металле и поэтому их называют также электронами проводимости. В приближении свободных электронов можно пренебречь силами взаимодействия между валентными электронами и ионными остовами и вести расчеты так, как если бы электроны были действительно свободными и без всяких ограничений могли перемещаться в любой области образца. Их полную энергию можно считать равной кинетической, а потенциальной можно пренебрегать.

Газ свободных, невзаимодействующих электронов, подчиняется принципу Паули, называют свободными, электронным газом Ферми.

Электроны, образующие в металлах электронный газ, по своим свойствам отличны от молекул газа. Поэтому и законы статистического распределения их различны: распределение молекул газа подчиняется классической статистике Максвелла- Больцмана, электронный газ – квантовой статистике Ферми- Дирака.

Для уяснения различия между статистиками отметим, прежде всего, что квантовой называют такую статистику, в которой учитывается неразличимость одинаковых частиц. Иначе говоря, в основу квантовой статистики положено квантовое определение состояния системы: должно быть указано, сколько частиц находится во всех квантовых состояниях (дискретность или непрерывность спектра здесь не имеет значения). Классическое определение состояния системы (статистики) состоит в том, что указывается, какие частицы находятся в данных состояниях, так как можно следить (в принципе) за их траекториями. Из классического определения можно получить формулу Больцмана и непосредственно, минуя квантовые законы. Такое деление статистик имеет глубокий смысл, заключающийся в том факте, что электроны обладают волновыми свойствами. Если в статистике Максвелла- Больцмана состояние частицы однозначно определяется заданием ее координат x, y, z и составляющих импульса p_x, p_y, p_z (поэтому состояние частиц здесь различимы), то в квантовой статистике невозможно различать два состояния x, y, z, p_x, p_y, p_z и x + dx, y + dy, z + dz, p_x+dp_x, p_y+dp_y _, p_z+dp_z, если

dxdydz dp_x dp_y dp_z < h³ (1)

где h – постоянная Планка (соотношение неопределенности Гейзенберга).

Произведение dxdydz dp_x dp_y dp_z = dt представляет собой элементарный объем шестимерного фазового пространства. Из соотношения (1) следует, что различным элементам фазового пространства dt будут соответствовать различные квантовые состояния электрона лишь в том случае, когда размер этих элементов не меньше h³. Поэтому в квантовой статистике за элементарную ячейку 6-мерного фазового пространства принимается объем, равный dt= h³.

При рассмотрении свободных электронов предполагается, что потенциальная энергия одинакова во всех точках металла, вследствие чего распределение в объеме V является равномерным. В этом случае вместо шестимерного фазового пространства x, y, z, p_x, p_y, p_z пользуются трехмерным пространством импульсов p_x, p_y, p_z и разбивают его на элементарные ячейки.

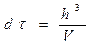(2)

Каждой такой ячейке соответствует отдельное квантовое состояние, отличимое от других состояний. Таким образом, метод деления фазового пространства на элементарные ячейки составляют одну из особенностей квантовой статистики.

Рассмотрим кусок металла объемом V, в котором находится N свободных электронов, образующих электронный газ. В пространстве импульсов каждой ячейке с объемом h³/V соответствует определенное квантовое состояние с энергией e. Функция распределения, которую предстоит найти, должна выражать вероятность заполнения этих ячеек электронами.

Получим искомое распределение, пользуясь методами статистической механики. Основной принцип здесь состоит в следующем. Если равновесная система может находиться в одном из N состояний, то вероятность того, что она находится в состоянии n с энергией e_n равна:

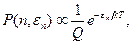(3)

где

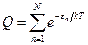
Здесь k – постоянная Больцмана; T – температура, Q - статистическая суммой.

Если i соответствует состоянию с энергией e_i, а A – квантовомеханический оператор наблюдаемой физической величины, то среднее значение этой величины равно:

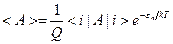Таким образом, состояние системы определяется указанием числа частиц n с энергией e. При этом возможны следующие значения чисел n = 0,1. То есть в случае Ферми-частиц в каждом состоянии может находиться не более одной частицы. Учитывая это, не трудно получить выражение для функции распределения Ферми – Дирака, основываясь на формуле (3), переписав ее в виде:

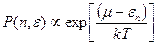(4)

Здесь m – химический потенциал.

Распределение Ферми - Дирака f(e) можно рассматривать как вероятность того, что одночастичное состояние с энергией e является занятым, когда система частиц, для которой указанное, состояние – одно из возможных - находится в тепловом равновесии при температуре T. Остается применить выражение (4) к случаю состояния, в котором может находиться не более одного электрона.

Когда состояние не занято, будем считать энергию равной нулю, отсюда следует, что P(0,0) = 1.

Когда состояние занято электроном, то

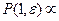
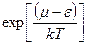
Следовательно, вероятность того, данное состояние занято, можно записать в виде:

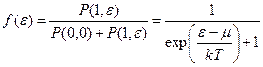(5)

Это и есть функция Ферми – Дирака.

Здесь m – химический потенциал, отнесенный к отдельной частице и равен:

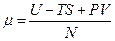
где U – внутренняя энергия системы; S – энтропия; V – объем системы; P – давление электронного газа; N – полное число электронов в системе.

Химический потенциал может быть измерен работой, которую нужно совершить, чтобы увеличить число частиц в системе на единицу. Величина m является функцией температуры; в каждый конкретной задаче m определяется из условия постоянства полного числа электронов в системе, т.е. из условия, что число электронов равно N. При абсолютном нуле m равно энергии Ферми e_F. При любой температуре T > 0 и при условии e=m функция f(e)=1/2. Отсюда энергию Ферми можно определить как энергию наиболее высокого, занятого электронами состояния при абсолютном нуле.

Область функции распределения, соответствующая большим значениям энергии, когда отвечает e - m >>kT большим значениям экспоненты в знаменателе (5); тогда единицей в знаменателе можно пренебречь и приближенно положить.

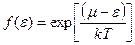
Эта функция близка к классической функции распределения Больцмана.

Функция распределения позволяет рассчитать число электронов, импульс (энергия) которых лежит в интервале p, p+dp (e, e + de). Перейдем к распределению по фазовому пространству частицы. При этом надо иметь в виду, что при данном значении импульса состояние частицы определяется также направлением ее спина. Поэтому число частиц в элементе фазового пространства dp_x dp_y dp_z dV равно:

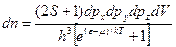(6)

где S – спин частицы.

Интегрируя по dV, получим распределение по компонентам импульса частиц, а, переходя к сферическим координатам в пространстве импульсов и интегрируя по углам, найдем распределение по абсолютной величине импульса

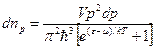(7)

где e=p²/2m, или распределение по энергии

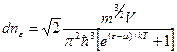(8)

Теперь нетрудно определить число электронов (термоэлектронов), выходящих под действием теплового возбуждения в единицу времени из поверхности металла. Проходить через поверхность металла могут только такие электроны, у которых нормальная к стенке составляющая скорости v_x больше некоторой величины v₀_x, удовлетворяющая неравенству.

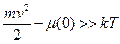(9)

Иначе говоря, энергия вылетающих электронов отличаются от граничной энергии гораздо больше, чем на kT.

Будем рассматривать металл как потенциальный ящик конечной глубины mv²₀_x/2. Так как тангенциальная составляющая скорости сохраняется при пересечении поверхности, то работа выхода со дна ящика равна mv²₀_x/2. С границы Ферми работа выхода равна mv²₀_x/2 - m. При нулевой температуре всегда имеются электроны с e > mv²₀_x/2; они, в основном, и выходят из металла.

Число электронов со скоростью v_x, падающих в секунду на квадратный сантиметр поверхности, равно v_xdn(v_x), где dn(v_x) – плотность электронов, имеющих данное значение скорости v_x. Запишем для плотности электронов, у которых составляющие скорости заключены в данном интервале – аналогично (6):

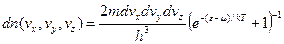, (10)

где 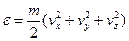. Через поверхность металла проходят только те электроны, для которых выполняется e - m >> kT. Поэтому можно перейти от распределения Ферми к распределению Больцмана с тем же значением m, как в распределении Ферми. Отсюда искомый поток электронов, вычисляемый по «хвосту» фермиевской кривой, где e - m >> kT, равен

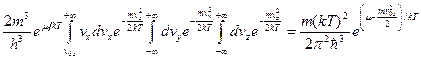(11)

Если приложить к металлу электрическое поле, то максимальный ток, который может быть снят с него при данной температуре (ток насыщения) определяется этой формулой. Отметим, что поскольку (11) относится к электронам в металле, то величина m» m_F, т.е. к граничной энергии при абсолютном нуле и не зависит от температуры.

Для изучения распределения термоэлектронов по скоростям в настоящей работе используется метод задерживающего потенциала. Если анод вакуумной лампы с накаленным катодом подавать отрицательное напряжение, препятствующее попаданию электронов на анод, то попадать на анод будут, лишь те термоэлектроны, энергия которых больше работы сил электрического поля торможению. Измеряя анодный ток при изменении величины отрицательного анодного напряжения, можно непосредственно исследовать распределение термоэлектронов по скоростям и энергиям. При расчете зависимости анодного тока i от отрицательного анодного напряжения U необходимо учитывать геометрию системы электронов.

Расчет для случая плоских электродов приводит к выражению:

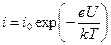(12)

где i₀ – сила тока при нулевой разности потенциалов между катодом и анодом;

e – заряд электрона.

Экспериментальную проверку формулы (12) удобно осуществлять построением графика зависимости ln(i) от величины анодного напряжения. Этот график является прямой линией, угловой коэффициент которой равен e/kT:

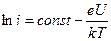(13)

Определив угловой коэффициент, можно рассчитать температуре, соответствующую состоянию электронного газа. Опыт показывает, что при термоэлектронной эмиссии электронный газ находится в тепловом равновесии с катодом, так что тем самым определяется температура катода. Выражения (12), (13) справедливы в случае плоских электродов. В настоящей работе используется радиолампа с коаксиальными цилиндрическими электродами, но с небольшой разницей радиусов анода и катода, что приводит лишь к незначительной систематической погрешности.

Так как анод и катод лампы изготовлены из разных материалов, то между ними имеется контактная разность потенциалов, изменяющаяся при изменении температуры катода. Контактная разность потенциалов, складывается алгебраически с приложенным напряжением. Знак и величину ее можно определить непосредственно по графикам, построенным в соответствии с формулой (13). Зависимость (13) имеет место лишь место при отрицательных разностях потенциалов между катодом и анодом (с учетом контактной разности потенциалов). При положительных разностях потенциалов возрастание тока замедляется, а в случае достижения точек насыщения прекращается. На рис. 1 показаны примерные зависимости ln(i) от U иллюстрирующие определение контактной разности потенциалов Dj между анодом и катодом путем экстраполяции обеих частей графика прямыми линиями до пересечения. После определения Dj можно построить график зависимости анодного тока от величины отрицательного анодного напряжения. Такой график показывает, какое число электронов обладает энергиями, большими определенной величины, соответствующей задерживающему анодному напряжению. От величины задерживающего напряжения U легко перейти к соответствующей составляющей скорости термоэлектронов, воспользовавшись соотношением.

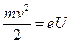(14)