Алгоритм Флойда – Уоршелла

Наиболее часто используемое название, метод получил в честь двух американских исследователей Роберта Флойда и Стивена Уоршелла, одновременно открывших его в 1962 году. Реже встречаются другие варианты наименований: алгоритм Рой – Уоршелла или алгоритм Рой – Флойда. Рой – фамилия профессора, который разработал аналогичный алгоритм на 3 года раньше коллег (в 1959 г.), но это его открытие осталось безвестным. Алгоритм Флойда – Уоршелла – динамический алгоритм вычисления значений кратчайших путей для каждой из вершин графа. Метод работает на взвешенных графах, с положительными и отрицательными весами ребер, но без отрицательных циклов, являясь, таким образом, более общим в сравнении с алгоритмом Дейкстры, т. к. последний не работает с отрицательными весами ребер, и к тому же классическая его реализация подразумевает определение оптимальных расстояний от одной вершины до всех остальных.

Для реализации алгоритма Флойда – Уоршелла сформируем матрицу смежности D [][] графа G =(V, E), в котором каждая вершина пронумерована от 1 до | V |. Эта матрица имеет размер | V |´| V |, и каждому ее элементу D [ i ][ j ] присвоен вес ребра, идущего из вершины i в вершину j. По мере выполнения алгоритма, данная матрица будет перезаписываться: в каждую из ее ячеек внесется значение, определяющее оптимальную длину пути из вершины i в вершину j (отказ от выделения специального массива для этой цели сохранит память и время). Теперь, перед составлением основной части алгоритма, необходимо разобраться с содержанием матрицы кратчайших путей. Поскольку каждый ее элемент D [ i ][ j ] должен содержать наименьший из имеющихся маршрутов, то сразу можно сказать, что для единичной вершины он равен нулю, даже если она имеет петлю (отрицательные циклы не рассматриваются), следовательно, все элементы главной диагонали (D [ i ][ i ]) нужно обнулить. А чтобы нулевые недиагональные элементы (матрица смежности могла иметь нули в тех местах, где нет непосредственного ребра между вершинами i и j) сменили по возможности свое значение, определим их равными бесконечности, которая в программе может являться, например, максимально возможной длинной пути в графе, либо просто – большим числом.

Ключевая часть алгоритма, состоя из трех циклов, выражения и условного оператора, записывается довольно компактно:

Для k от 1 до | V | выполнять

Для i от 1 до | V | выполнять

Для j от 1 до | V | выполнять

Если D [ i ][ k ]+ D [ k ][ j ]< D [ i ][ j ] то D [ i ][ j ] ← D [ i ][ k ]+ D [ k ][ j ]

Кратчайший путь из вершины i в вершину j может проходить, как только через них самих, так и через множество других вершин k ∈(1, …, | V |). Оптимальным из i в j будет путь или не проходящий через k, или проходящий. Заключить о наличии второго случая, значит установить, что такой путь идет из i до k, а затем из k до j, поэтому должно заменить, значение кратчайшего пути D [ i ][ j ] суммой D [ i ][ k ]+ D [ k ][ j ].

Рассмотрим полный код алгоритма Флойда – Уоршелла на C++ и Паскале, а затем детально разберем последовательность выполняемых им действий.

Код программы на C++:

const int maxV=1000;

int i, j, n;

int GR[maxV][maxV];

void FU(int D[][maxV], int V) //алгоритм Флойда-Уоршелла

{

int k;

for (i=0; i<V; i++) D[i][i]=0;

for (k=0; k<V; k++)

for (i=0; i<V; i++)

for (j=0; j<V; j++)

if (D[i][k] && D[k][j] && i!=j)

if (D[i][k]+D[k][j]<D[i][j] || D[i][j]==0)

D[i][j]=D[i][k]+D[k][j];

for (i=0; i<V; i++)

{

for (j=0; j<V; j++) cout<<D[i][j]<<"\t";

cout<<endl;

}

}

void main() //главная функция

{

cout<<"Количество вершин в графе > "; cin>>n;

cout<<"Введите матрицу весов ребер:\n";

for (i=0; i<n; i++)

for (j=0; j<n; j++)

{

cout<<"GR["<<i+1<<"]["<<j+1<<"] > ";

cin>>GR[i][j];

}

cout<<"Матрица кратчайших путей:"<<endl;

FU(GR, n);

}

Код программы на Pascal:

const maxV=1000;

type matr=array[1..maxV, 1..maxV] of integer;

var i, j, n, inf: integer;

GR: matr;

Procedure FU(D: matr; V: integer); {алгоритм Флойда-Уоршелла}

var k: integer;

begin

inf:=1000000;

for i:=1 to V do D[i, i]:=0;

for k:=1 to V do

for i:=1 to V do

for j:=1 to V do

if (D[i, k]<>0) and (D[k, j]<>0) and (i<>j) then

if (D[i, k]+D[k, j]<D[i, j]) or (D[i, j]=0) then

D[i, j]:=D[i, k]+D[k, j];

for i:=1 to V do

begin

for j:=1 to V do

write(D[i, j]:4);

writeln;

end;

end;

begin {главный блок программы}

write('Количество вершин в графе > ');

readln(n);

writeln('Введите матрицу весов ребер:');

for i:=1 to n do

for j:=1 to n do

begin

write('GR[', i, '][', j, '] > ');

read(GR[i, j]);

end;

writeln('Матрица кратчайших путей:');

FU(GR, n);

end.

Положим, что в качестве матрицы смежности, каждый элемент которой хранит вес некоторого ребра, была задана следующая матрица:

Количество вершин в графе, представлением которого является данная матрица, равно 3, и, причем между каждыми двумя вершинами существует ребро. Ниже показан граф этой матрицы смежности (рис. 9.11).

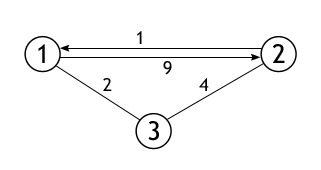
Рисунок 9.11 – Смешанный граф

Задача алгоритма: перезаписать данную матрицу так, чтобы каждая ячейка вместо веса ребра из i в j, содержала кратчайший путь из i в j. Для примера взят совсем маленький граф, и поэтому не будет не чего удивительного, если матрица сохранит свое изначальное состояние. Но результат тестирования программы показывает замену двух значений в ней. Таблица (рис. 9.12) поможет с анализом этого конкретного примера.

Рисунок 9.12 – Нахождением оптимальных расстояний для графа 8.11

В данной таблице показаны 27 шагов выполнения основной части алгоритма. Их столько по той причине, что время выполнения метода равно O (| V |³). Наш граф имеет 3 вершины, а 3³=27. Первая замена происходит на итерации, при которой k =1, i =2, а j =3. В тот момент D [2][1]=1, D [1][3]=2, D [2][3]=4. Условие истинно, т. е. D [1][3]+ D [3][2]=3, а 3<4, следовательно, элемент матрицы D [2][3] получает новое значение. Следующий шаг, когда условие также истинно привносит изменения в элемент, расположенный на пересечении второй строки и третьего столбца.