В случае, если параметры потока не терпят разрыва, и могут быть описаны функциями непрерывными со своими производными, удобно использовать законы сохранения в виде дифференциальных уравнений в частных производных. Для перехода к такой форме записи от интегральной, используют теорему Остроградского – Гаусса (1.4.7). Подобный подход был подробно рассмотрен при выводе уравнения неразрывности:
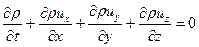 . (1.4.13)
. (1.4.13)
Привлекая формулы Коши (1.5.3) и применяя теорему Остроградского – Гаусса получим:
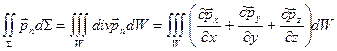 .
.
Подставляя их в интегральную форму записи закона сохранения импульса (1.6.18) имеем:
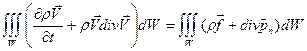 , (1.6.21)
, (1.6.21)
Учитывая, что объем 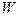 – произволен, получим векторное уравнение в частных производных – дифференциальную форму записи закона сохранения импульса, которую принято называть уравнениями движения сплошной среды в напряжениях:
– произволен, получим векторное уравнение в частных производных – дифференциальную форму записи закона сохранения импульса, которую принято называть уравнениями движения сплошной среды в напряжениях:
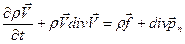 , (1.6.22)
, (1.6.22)
расписывая по координатам:
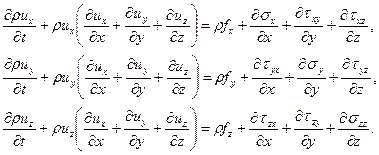 (1.6.23)
(1.6.23)
Компоненты тензора напряжений для случая ньтоновской жидкости (1.5.23):
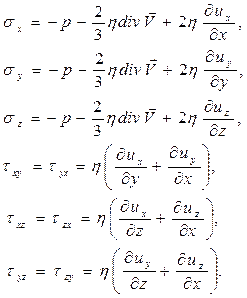 (1.6.24)
(1.6.24)
Подставляя (1.6.24) в (1.6.23) и используя уравнение неразрывности (1.4.13), получим систему уравнений движения для вязкой сжимаемой жидкости, которая носит название системы уравнений Навье-Стокса:
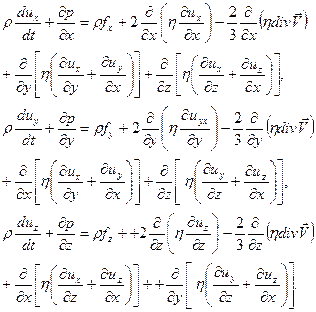 (1.6.25)
(1.6.25)
Повторяя процедуру перехода к интегралу по объему для закона сохранения энергии имеем:
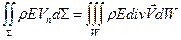 ,
, 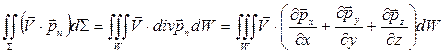 ,
,
Используя эти соотношения, получим еще одну форму записи закона сохранения энергии:
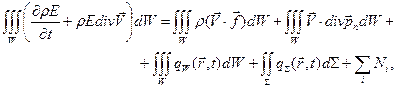
Для перехода к дифференциальной форме записи, необходимо ввести понятие вектора теплового потока:

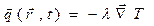 , (1.6.26)
, (1.6.26)
где 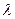 - коэффициент теплопроводности,
- коэффициент теплопроводности, 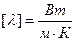 ;
; 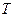 - абсолютная температура. Знак минус показывает, что тепло передается от более нагретого тела к менее нагретому.
- абсолютная температура. Знак минус показывает, что тепло передается от более нагретого тела к менее нагретому.
Соответственно:
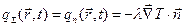 ,
,
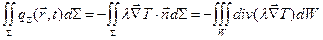 ,
,
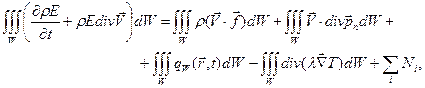 (1.6.27)
(1.6.27)
Или в дифференциальной форме без учета устройств, изменяющих механическую энергию потока, уравнение энергии для вязкой теплопроводной сплошной среды:
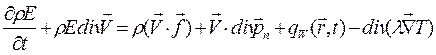 . (1.6.28)
. (1.6.28)
В итоге, для описания движения вязкой сплошной сжимаемой среды может быть использована система дифференциальных уравнений в частных производных, состоящая из уравнения неразрывности (1.4.13), уравнений Навье-Стокса (1.6.25), уравнения энергии (1.6.28) и уравнения состояния среды.
Для несжимаемой среды система имеет более простой вид. Уравнение неразрывности переходит в уравнение несжимаемости (1.4.4), уравнения Навье-Стокса и энергии существенно упрощаются, уравнение состояния становится не нужным:
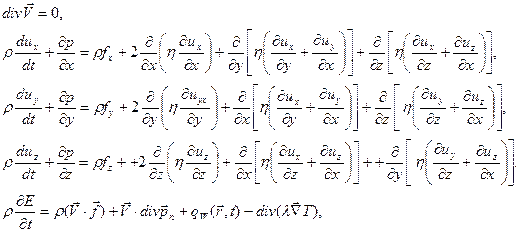 (1.6.29)
(1.6.29)
1.9. Основы теории размерностей и подобия. 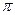 - теорема. Подобие физических явлений, моделирование.
- теорема. Подобие физических явлений, моделирование.
Под математической моделью явления обычно понимают его описание с помощью уравнений с соответствующими начальными и граничными условиями. Для большинства явлений, встречающихся на практике и связанных с течением газов и жидкостей, решение таких моделей не может быть получено с достаточной точностью в виде аналитических зависимостей от исходных данных. Это обусловлено существенной нелинейностью данных процессов. В этих случаях приходится прибегать к их изучению на моделях. Моделирование принято разделять на физическое, аналоговое и численное моделирование.
Под физическим моделированием обычно понимают экспериментальные исследования на лабораторных установках в условиях максимально приближенных к реальным. Примером таких установок являются аэродинамические трубы, гидробассейны, гидролотки и др. Создание модели самолета, корабля, плотины в натуральную величину требует больших затрат и не гарантирует положительного результата. Поэтому создают их копии, которые и испытывают. Снимая характеристики, корректируют исходные конструкции.
Явление может быть исследовано и на моделях другой физической природы, если их математическое описание (системы уравнений, граничные и начальные условия) одинаково. Такое моделирование называется аналоговым. Например, диффузия и теплопроводность. Оба процесса описываются параболическим уравнением в частных производных второго порядка. Измерение концентрации затруднено, зачастую требуется отбор проб и их последующий физико-химический анализ. Измерение температуры существенно проще, часто достаточно поставить в нужную точку термопару. Часто удается собрать электронную схему явления. Так распределение тока в системе проводников, описывается системой уравнений Кирхгофа, так же как распределение потоков сплошной среды в системе трубопроводов. Ясно, что создание электронной схемы проще, чем трубопроводной.
Если математические уравнения, описывающие процесс, известны, но не имеют аналитического решения, используют их численные модели, которые можно (не всегда) решить на электронных вычислительных машинах (компьютерах).
В любом случае стоит вопрос о переносе полученных данных на реальный объект. Это возможно, если имеет место гидродинамическое (геометрическое, кинематическое и динамическое) подобие между объектом и моделью.
Геометрически подобными называются объекты, для которых все соответствующие линейные размеры находятся в одинаковом соотношении:
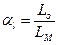 , (1.7.1)
, (1.7.1)
где 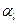 - линейный масштабный коэффициент (линейный масштаб), индекс «о» - соответствует натурному объекту, «М» - модельному объекту. Очевидно, что в этом случае все угловые значения одинаковы для объекта и модели.
- линейный масштабный коэффициент (линейный масштаб), индекс «о» - соответствует натурному объекту, «М» - модельному объекту. Очевидно, что в этом случае все угловые значения одинаковы для объекта и модели.
Кинематически подобными называются явления, для которых отношение скоростей и их направление одинаковы:
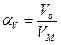 . (1.7.2)
. (1.7.2)
Соответственно, линейные ускорения, угловые скорости и ускорения, а также время прохождения частиц между двумя соответствующими точками так же находятся в одинаковых соотношениях:
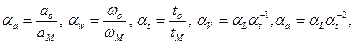 (1.7.3)
(1.7.3)
Динамически подобными называются явления, для которых все силы, действующие на соответствующие частицы сплошной среды, и следовательно силы действующие на тела, имеют одинаковое отношение и направление:
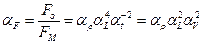 . (1.7.4)
. (1.7.4)
Здесь 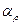 - линейный масштаб плотности, для жидкости
- линейный масштаб плотности, для жидкости  .
.
Критерием подобия называется безразмерный комплекс, состоящий из размерных величин, определяющий рассматриваемое физическое явление.
Преобразуем (1.7.4) заменив масштабные коэффициенты их выражениями через размерные параметры:
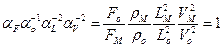 .
.
Или в другом виде:
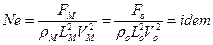 . (1.7.5)
. (1.7.5)
Здесь 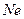 - носит название критерия Ньютона, (
- носит название критерия Ньютона, (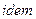 (лат.) – «то же самое»).
(лат.) – «то же самое»).
Таким образом, для полного динамического подобия двух гидродинамических потоков требуется равенство критериев Ньютона для них. При физическом моделировании обычно не удается добиться полного динамического подобия (в силу различной физической природы сил действующих в сплошной среде), в этом случае выделяют одну главную (определяющую) силу и пренебрегают действием остальных. Такое подобие называется частичным динамическим подобием. Если в качестве таковой выбрана сила тяжести, то используется критерий Фруда:
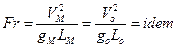 . (1.7.6)
. (1.7.6)
Если определяющими являются силы инерции, то применяют критерий Рейнольдса:
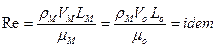 . (1.7.7)
. (1.7.7)
В случае если течение определяется силами давления, применим критерий Эйлера:
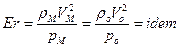 . (1.7.8)
. (1.7.8)
Для сил поверхностного натяжения – критерий Вебера:
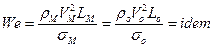 . (1.7.9)
. (1.7.9)
Рассмотрим вопрос о количестве критериев необходимых для полного подобия. Все физические величины делятся на размерные и безразмерные. Из размерных величин можно выделить основные, независимые друг между собой, и производные, которые могут быть выражены через основные величины. В механике за основные величины принимают длину 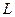 , массу
, массу 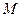 , время
, время 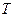 . Размерность производной величины обозначается квадратными скобками. Так размерность силы
. Размерность производной величины обозначается квадратными скобками. Так размерность силы 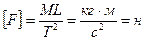 . Моделирование явления требует предварительного анализа размерностей, в процессе которого размерные параметры, определяющие процесс, сводятся к набору безразмерных комплексов. Этот анализ может быть облегчен с помощью
. Моделирование явления требует предварительного анализа размерностей, в процессе которого размерные параметры, определяющие процесс, сводятся к набору безразмерных комплексов. Этот анализ может быть облегчен с помощью 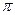 - теоремы.
- теоремы.
Любая функциональная зависимость между 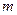 - размерными величинами может быть представлена в виде другой зависимости между
- размерными величинами может быть представлена в виде другой зависимости между 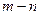 безразмерными комплексами, где
безразмерными комплексами, где 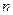 - число основных размерных величин.
- число основных размерных величин.
Как мы уже отметили для механики и следовательно для гидравлики 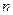 =3. Пусть некоторое явление описывается размерной зависимостью:
=3. Пусть некоторое явление описывается размерной зависимостью:
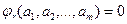 , (1.7.10)
, (1.7.10)
В соответствии с 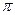 - теоремой она может быть заменена на другую зависимость:
- теоремой она может быть заменена на другую зависимость:
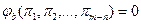 , (1.7.11)
, (1.7.11)
где 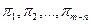 - безразмерные комплексы, составленные из размерных параметров
- безразмерные комплексы, составленные из размерных параметров 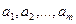 . Каждый комплекс представляет собой произведение из
. Каждый комплекс представляет собой произведение из 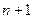 размерных параметров, возведенных в некоторую степень, которые заранее неизвестны:
размерных параметров, возведенных в некоторую степень, которые заранее неизвестны:
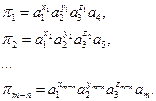 (1.7.12)
(1.7.12)
Поскольку комплексы 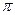 безразмерные можно записать:
безразмерные можно записать:
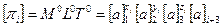 . (1.7.13)
. (1.7.13)
Рассмотрим в качестве примера процесс обтекания твердого тела жидкость. На тело действует сила 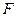 , величина которой зависит от скорости набегающего потока
, величина которой зависит от скорости набегающего потока 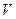 , плотности жидкости
, плотности жидкости 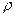 , ее динамической вязкости
, ее динамической вязкости 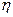 , и характерного размера
, и характерного размера 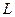 , тогда зависимость:
, тогда зависимость:
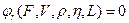 , (1.7.14)
, (1.7.14)
может быть заменена на следующую:
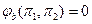 . (1.7.15)
. (1.7.15)
Выберем в качестве первых 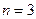 сомножителей
сомножителей 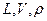 , тогда:
, тогда:
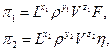
Учитывая размерность определяющих явление величин:
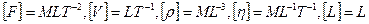 ,
,
получим:
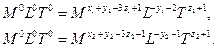
Откуда вытекают две системы линейных уравнений:
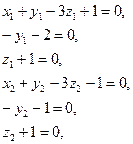
Решением которых будет: 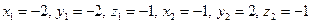 . Следовательно:
. Следовательно:
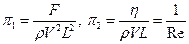 .
.
Ясно, что сила воздействия на тело жидкости (сила сопротивления) будет:
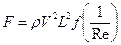 . (1.7.16)
. (1.7.16)
Тот же результат можно представить и в безразмерном виде вводя характерную площадь тела (площадь миделя) 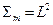 и коэффициент сопротивления тела
и коэффициент сопротивления тела 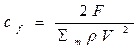 :
:
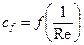 . (1.7.17)
. (1.7.17)
Так для обтекания вязкой ньютоновской жидкостью шара, для малых значений чисел Рейнольдса, Стоксом было получена аналитическая зависимость:
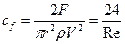 . (1.7.18)
. (1.7.18)
 2015-02-04
2015-02-04 1340
1340








