Приведенная теплота

Для обратимого цикла Карно коэффициент полезного действия можно вычислить по любой из полученных ранее формул

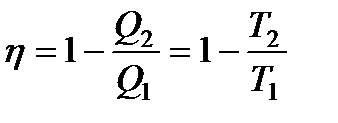. (134)

Отсюда

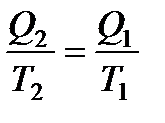(135)

Или

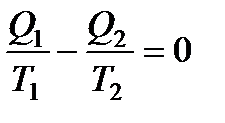. (136)

Поскольку Q₁ и Q₂ имеют разные знаки, то выражение (136) можно переписать в виде

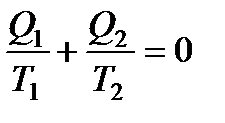, (137)

где величина Q считается положительной, если теплота передается рабочему телу, и отрицательной, если теплота отнимается.

Отношение количества теплоты, подведенной к системе, к температуре, при которой это происходит, называется приведенной теплотой. Таким образом, 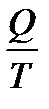–приведенная теплота, передаваемая системе. 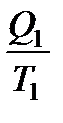– приведенная теплота в 1-м изотермическом процессе, 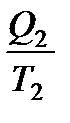– приведенная теплота во 2-м изотермическом процессе. На адиабатических участках цикла Карно теплообмена с окружающей средой нет: Q=0. Следовательно, формула (137) учитывает всю теплоту, участвующую в цикле Карно. Таким образом, для обратимого цикла Карно

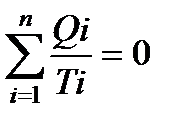. (138)

Так как любой замкнутый цикл можно представить как сумму бесконечного числа циклов Карно, то для любого замкнутого обратимого цикла выражение (138) будет справедливо и его можно записать в следующем виде

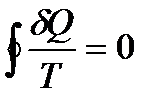. (139)

Последнее соотношение носит название равенства Клаузиуса.

КПД любого другого цикла меньше, чем КПД обратимого цикла Карно. Отсюда получаем:

.

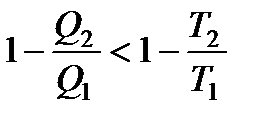В итоге все вышеприведенные равенства превращаются в неравенства:

.

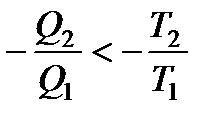
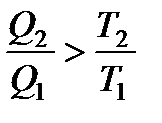
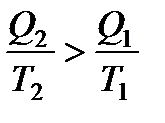
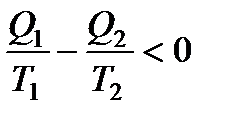Учитывая, что теплота – величина алгебраическая, в итоге получаем:

,

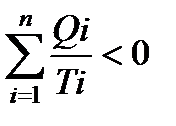или

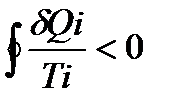(140)

Уравнение (140) называется неравенством Клаузиуса.

Объединяя (139) и (140), можно записать

,

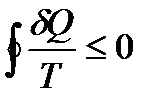где знак равенства относится к обратимому процессу, а знак неравенства – к необратимому.

Таким образом, сумма приведенных теплот любого цикла равна нулю (обратимый процесс) или меньше нуля (необратимый процесс).