Перечислимые и разрешимые множества

При использовании далее терминов «алгоритм», «вычислимая функция» имеется в виду любая возможная их формализация в терминах машин Тьюринга, нормальных алгорифмов или рекурсивных функций. Все рассматриваемые множества – суть подмножества натурального ряда. Дополнением множества MÌ N является множество N\ M.

Определение 5.1.1. Множество MÌ N называется разрешимым, если существует алгоритм, позволяющий для каждого nÎ N определить, принадлежит ли это число множеству M или нет. Такой алгоритм называется разрешающим для множества M.

В иной терминологии это определение формулируется так.

Определение 5.1.1*. Множество MÌ N называется разрешимым, если его характеристическая функция:

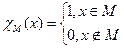
является общерекурсивной.

Теорема 5.1.1. Если множества А и В разрешимы, то разрешимы множества N\ А, АÈВ, АÇВ.

Доказательство. Если характеристические функци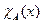и и 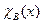– общерекурсивны, то и характеристические функции множеств N\ А, АÈВ, АÇВ:

,

.

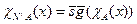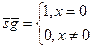
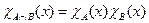
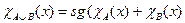также являются общерекурсивными функциями.

Теорема 5.1.2. Любое конечное множество MÌ N – разрешимо.

Определение 5.1.2. Непустое множество MÌ N перечислимо, если существует алгоритм, перечисляющий (порождающий) его элементы. Этот алгоритм называют порождающим алгоритмом для множества M.

Пустое множество считается перечислимым по определению.

В терминологии рекурсивных функций приведенное определение формулируется так.

Определение 5.1.2*. Непустое множество MÌ N перечислимо, если существует общерекурсивная функция j _M (x) такая, что: M={ y: y=j _M (x), xÎ N }.

Теорема 5.1.3. Если множества А и В перечислимы, то перечислимо множество АÈВ.

Доказательство. Положим

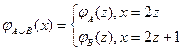
Так как функция rest (x, 2) нахождения остатка от деления x на 2 является общерекурсивной (доказательство этого факта остается за читателем), то общерекурсивной будет и функция:

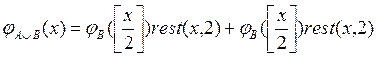, где 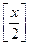– целая часть числа .

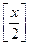В этом случае множество

АÈВ={ y: 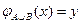, xÎ N }

по определению будет перечислимым.

¨Теорема доказана.

Теорема 5.1.4. Если множества А и В перечислимы, то перечислимо множество АÇВ.

Доказательство. Введем в рассмотрение следующие функции:

1) функцию ограниченного вычитания:

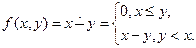
2) функции большого размаха:

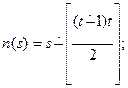
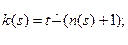
где .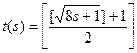

3) 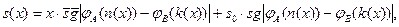где:

j _A (x) – общерекурсивная функция, порождающая множество A;

j _B (x) – общерекурсивная функция, порождающая множество B;

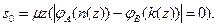
Все перечисленные функции являются общерекурсивными, и потому общерекурсивной функцией будет функция j _AÇB (x)=j _A (n(s(x))), порождающая множество AÇB.

¨Теорема доказана.

Теорема 5.1.5. Непустое разрешимое множество MÌ N перечислимо.

Доказательство. Пусть 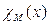– характеристическая функция множества MÌ N, 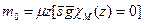. Тогда функция

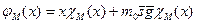
является общерекурсивной и порождающей множество М.

Если М={ m₀, m₁, m₂, …, m_n,.. } и m₀,<m₁<m₂ <…<m_n, то график функции 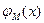имеет вид:

Теорема 5.1.6. Множество MÌ N разрешимо тогда и только тогда, когда Mи N\ М перечислимы.

Доказательство. Если множество M разрешимо, то по теореме 5.1 разрешимо его дополнение N\ М. По теореме 5.4 перечислимы оба множества. В одну сторону теорема доказана.

Пусть далее Mи N\ М перечислимы, что означает существование общерекурсивных функций j _М, j _{N\ М}.

Определим общерекурсивную функцию s(x), значением которой является наименьшее число z, при котором либо j _М (z)= x, либоj _{N\ М} (z)= x, следующим образом: .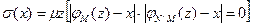

Тогда характеристическая функция множества М может быть записана так: 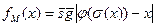. Так как: 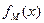общерекурсивная функция, то теорема доказана.

Следствие. Если множество M перечислимо, но неразрешимо, то множество N\ М не перечислимо.

Теорема 5.1.7. Множество записей машин Тьюринга является перечислимым множеством.

Теорема 5.1.8. Множество записей самоприменимых машин Тьюринга перечислимо, но не разрешимо.

Следствие. Дополнение множества записей самоприменимых машин Тьюринга неперечислимо.