Отношение эквивалентности

Бинарное отношение называется эквивалентностью, если оно рефлексивно, симметрично и транзитивно. Эквивалентность обозначается символом ~, например, х ~ y. Граф отношения эквивалентности есть полный граф, заданный на множестве А, т.е. множество ребер графа отношения эквивалентности либо равно А², либо несвязный граф, каждая компонента связности которого является полным подграфом графа на некотором подмножестве вершин графа, образующем класс эквивалентности для данного отношения. Вообще, классом эквивалентности для отношения ~ на множестве А по элементу а называется множество, определенное следующим образом:

X({a})={x | x~ а, xÎA }.

Разумеется, элемент а, для которого класс эквивалентности определен таким образом, также входит в этот класс в силу рефлексивности отношения эквивалентности.

Множество классов эквивалентности связано с разбиением несущего множества. Вообще разбиением множества М называется множество, элементами которого являются множества подмножества М; объединение этих подмножеств равно М, а пересечения попарно пусты. Пустое множество не входит в разбиение.

Можно доказать, что отношение эквивалентности “~” на А образует разбиение А/ ~ множества А, причем элементами разбиения являются классы эквивалентности. Разбиение называется минимальным, если в каждый класс эквивалентности входит по одному элементу. Примером такого отношения является отношение х ~ у Û х=у, х,у Î А. Разбиение называется максимальным, если оно образует единственный класс эквивалентности, в который входят все элементы А.

Множество классов эквивалентности элементов множества А по эквивалентности “~” называется фактор-множеством А по “~”, обозначается A/~.

Примерами отношений эквивалентности являются отношения равенства чисел (образует максимальное разбиение), конгруэнтности треугольников (классы эквивалентности включают все конгруэнтные треугольники), равенства множеств, равномощности множеств, сравнимости чисел по модулю m (это отношение определяет множества чисел, дающих одинаковый остаток при делении на m).

Теорема. Если “~” – отношение эквивалентности, заданное на произвольном непустом множестве А, то существует разбиение R _~ = {A_x | xÎ A}- такое, что каковы бы ни были x,yÎ A, x ~ y тогда и только тогда, когда х и у принадлежат к одному и тому же классу разбиения.

§ Пусть ~ - эквивалентность на А и A/~= {A_x | xÎ A}- фактор-множество А по отношению ~. Докажем существование разбиения R _~, равного фактор множеству A/~.

· Пусть aÎA – произвольный элемент А. Обозначим А_а = {x | x Î A, x ~ a} – класс эквивалентности по элементу а. Тогда аÎА_а, и, следовательно 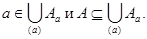Так как элемент а выбирается произвольно, и каждый класс эквивалентности содержит только элементы множества А, то 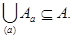Из существования двух включений следует, что 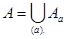. Следовательно объединение классов эквивалентности равно А.

· Докажем теперь, что попарные пересечения классов эквивалентности пусты. Пусть a,b Î A, aÎ A_a, b Î A_b, A_a и A_b –два класса эквивалентности. Пусть А_a Ç A_b ¹Æ. Тогда существует хотя бы один элемент сÎА такой, что с Î А_a и с Î А_b, т.е. с ~ a и c ~ b. Пусть z – произвольный элемент множества А_а. Тогда z ~ a и а ~ с. По свойству транзитивности отношения эквивалентности получаем z ~ c. Но с ~ b, следовательно, по свойству транзитивности z ~ b. Следовательно, z Î A_b. Следовательно, A_a Í A_b. Обратное включение доказывается аналогично. Следовательно, пересечение A_a и A_b не пусто тогда и только тогда, когда это одно и то же множество.

Таким образом, доказано, что множество классов эквивалентности образуют разбиение множества А. ¨

Таблица 2 Свойства отношения эквивалентности

Понятие	Свойство или определение	Пояснение
~ - отношение эквивалентности на А	· ~Í А´А · ~ рефлексивно в А · ~ транзитивно в А · ~ симметрично в А	dom ~ = rng ~ = A ~ · ~ = ~ ~ = ~-1.
Aa- класс эквивалентности отношения ~ по элементу а	~ ({a}) = {x | (a,x) Î ~ }	Множество всех элементов, таких, что x ~ a. Каждый класс эквивалентности определен заданием одного элемента.
Разбиение множества А	Z={Z1,Z2, …, ZN}, Æ Ï Z,	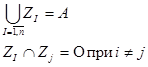Разложение множества А на непересекающиеся непустые подмножества, так что каждый элемент из А принадлежит одному и только одному из этих подмножеств.