Л. П. СЕМИХИНА,
А. В. ШИРШОВА,
В.И. СЕМИХИН
МОЛЕКУЛЯРНАЯ ФИЗИКА
ЯВЛЕНИЯ ПЕРЕНОСА
МЕТОДИЧЕСКИЕ УКАЗАНИЯ ДЛЯ СТУДЕНТОВ 1КУРСА
РОССИЙСКАЯ ФЕДЕРАЦИЯ
МИНИСТЕРСТВО ОБЩЕГО И ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
ТЮМЕНСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
ФИЗИЧЕСКИЙ ФАКУЛЬТЕТ
Кафедра механики многофазных систем
Л. П. Семихина
А. В. Ширшова,
В.И. Семихин
МОЛЕКУЛЯРНАЯ ФИЗИКА
ЯВЛЕНИЯ ПЕРЕНОСА
МЕТОДИЧЕСКИЕ УКАЗАНИЯ ДЛЯ СТУДЕНТОВ 1КУРСА
ИЗДАТЕЛЬСТВО ТЮМЕНСКОГО ГОСУНИВЕРСИТЕТА 2002 г.
Явления переноса в газах
I. Теория явлений переноса в газах.
Средняя скорость теплового движения газовых молекул определяется формулой
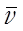 =
= 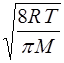 (1)
(1)
Уже при комнатной температуре она порядка скорости ружейной пули. Например, при Т=293К для паров воды средняя скорость движения ее молекул равна 587м/с, для воздуха - 462,5 м/с. На ранней стадии развития молекулярно-кинетической теории газов столь большие значения скоростей молекул некоторым физикам казались невозможными. Если скорости молекул действительно так велики – говорили они, - то запах пахучего вещества должен был бы распространяться от одного конца комнаты к другому практически мгновенно. На самом деле при отсутствии конвективных потоков воздуха время распространения запаха на такие расстояния может составлять многие минуты, и даже часы. Распространение запаха осуществляется посредством медленного процесса диффузии.
1.1. Средняя длина свободного пробега молекул.
Медленность процесса диффузии и аналогичных ей явлений Клаузиус объяснил столкновениями молекул. Молекула газа движется свободно только на коротком расстоянии между столкновениями с другими молекулами. В момент столкновения скорость молекулы резко меняется как по модулю, так и по направлению. В результате молекула беспорядочно мечется, а ее общее продвижения по какому-то направлению происходит сравнительно медленно. Для количественного описания явления Клаузиус ввел понятие с редней длины свободного пробега, равной среднему расстоянию, которое проходит молекула между столкновениями.
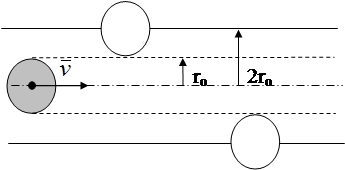 Для вычисления средней длины свободного пробега воспользуемся моделью твердых шаров. Между столкновениями молекулы-шары движутся прямолинейно и равномерно. Для упрощения расчета рассмотрим сначала случай, когда движется только одна молекула, а молекулы мишени, с которыми она сталкивается - неподвижны. Как видно из рисунка данная молекула столкнется с N молекулами, находящимися внутри цилиндра радиусом 2ro, где ro - радиус молекулы. Если число молекул в единице объема no, а длина цилиндра
Для вычисления средней длины свободного пробега воспользуемся моделью твердых шаров. Между столкновениями молекулы-шары движутся прямолинейно и равномерно. Для упрощения расчета рассмотрим сначала случай, когда движется только одна молекула, а молекулы мишени, с которыми она сталкивается - неподвижны. Как видно из рисунка данная молекула столкнется с N молекулами, находящимися внутри цилиндра радиусом 2ro, где ro - радиус молекулы. Если число молекул в единице объема no, а длина цилиндра 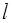 , то
, то
N= 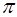 (2ro)2no
(2ro)2no 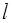 =
= 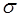 no
no 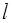 , (2)
, (2)
где величина 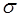 =
= 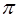 (2ro)2 - называется поперечным сечением рассеяния. При N = 1 длина цилиндра
(2ro)2 - называется поперечным сечением рассеяния. При N = 1 длина цилиндра 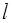 равна средней длине свободного пробега
равна средней длине свободного пробега 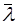 . В таком случае из (2) имеем
. В таком случае из (2) имеем
 = 1/
= 1/ 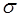 no (3)
no (3)
За время 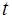 = 1сек молекула перемещается на расстояние равное
= 1сек молекула перемещается на расстояние равное 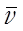 =
= 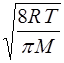 , претерпевая столкновения через
, претерпевая столкновения через  =1/
=1/ 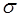 no.
no.
Отношение 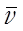 /
/  =
= 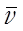
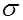 no = Z (4)
no = Z (4)
– есть число столкновений данной молекулы за время 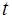 = 1сек.
= 1сек.
 Учесть тот фактор, что двигается не только рассматриваемая молекула, но и молекулы мишеней, с которыми она сталкивается, можно достаточно просто, заменив в выражении (4)
Учесть тот фактор, что двигается не только рассматриваемая молекула, но и молекулы мишеней, с которыми она сталкивается, можно достаточно просто, заменив в выражении (4)  на
на 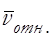 - среднее значение относительной скорости 2-х сталкивающихся между собой молекул. В таком случае
- среднее значение относительной скорости 2-х сталкивающихся между собой молекул. В таком случае
Z = 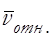
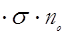 (5)
(5)
По определению 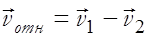 , т.е. вектор
, т.е. вектор 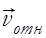 равен векторной сумме двух векторов
равен векторной сумме двух векторов 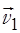 и
и 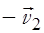 . Длину вектора
. Длину вектора 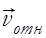 можно найти по теореме косинусов:
можно найти по теореме косинусов:
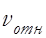 =
= 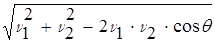
-где 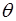 -угол между векторами
-угол между векторами  и
и 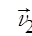
Учитывая, что среднее значение 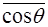 = 0, а
= 0, а 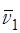 =
= 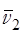 =
=  , получаем:
, получаем: 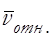 =
= 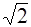
 (6)
(6)
Подставляя данное выражение в (5), имеем
Z = 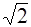

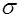 no (7)
no (7)
Подставляя в соотношения (4) найденное для Z значение, получаем окончательное выражение для 
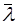 =
=  / Z =
/ Z = 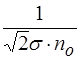 =
= 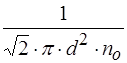 (8)
(8)
где 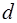 - диаметр молекулы.
- диаметр молекулы.
1.2. Общее уравнение переноса.
Упрощенный вывод. Система, предоставленная самой себе, стремится достигнуть наиболее вероятного равновесного состояния. В результате данного процесса все параметры системы достигают равновесных значений. Этот процесс описывается как перенос соответствующих молекулярных свойств. Нет смысла рассматривать каждое явление переноса в отдельности, получим обобщенное уравнение переноса.
Пусть G характеризует некоторое молекулярное свойство, отнесенное к одной молекуле. Этим свойством может быть энергия, импульс, концентрация и т.д. Рассмотрим площадку с площадью dS, перпендикулярную оси Х и находящейся в точке с координатой х.
 В упрощенном выводе принимается, что молекулы, двигаясь в направлении выделенной площадки из точек с координатой x +
В упрощенном выводе принимается, что молекулы, двигаясь в направлении выделенной площадки из точек с координатой x +  и x-
и x-  , где
, где 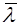 - средняя длина свободного пробега молекул, не претерпевают столкновений между собой во время этого движения. В таком случае, при столкновении с площадкой dS эти молекулы будут передавать ей свойство, которое они имели в точке с координатой x+
- средняя длина свободного пробега молекул, не претерпевают столкновений между собой во время этого движения. В таком случае, при столкновении с площадкой dS эти молекулы будут передавать ей свойство, которое они имели в точке с координатой x+  и x-
и x-  , т.е. G(x
, т.е. G(x 
 ). Т.к.
). Т.к.  мало, величину G(x
мало, величину G(x 
 ) можно разложить в ряд Тейлора, ограничившись первым членом разложения: G(x
) можно разложить в ряд Тейлора, ограничившись первым членом разложения: G(x 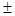
 )=G(x)
)=G(x) 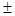
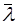
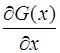 (9)
(9)
Будем считать равновероятными все возможные направления движения. Тогда, как в положительном, так и отрицательном направлении оси Х, будет двигаться одинаковое количество молекул, равное 1/6 от всех молекул. Количество молекул dN, которое столкнется с площадкой dS за время dt, равно 1/6 от числа молекул, находящихся в объеме V=  dS dt.
dS dt.
Тогда dN = 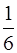 no
no  dS dt, где no - число молекул в единице объема
dS dt, где no - число молекул в единице объема
Количество молекул, пересекающих единичную площадку в единицу времени (dS=1, dt=1), называется потоком молекул IN.
Поток молекул в положительном направлении оси Х равен
IN(+)= 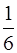 no
no  (10)
(10)
Каждая молекула, двигаясь в положительном направлении оси Х и сталкиваясь с площадкой dS, будет передавать ей свойство G(x -  ), которое она имела в точке с координатойx -
), которое она имела в точке с координатойx -  .В таком случае поток свойства G в положительном направлении оси Х равен:
.В таком случае поток свойства G в положительном направлении оси Х равен:
IG(+) = 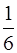 no
no  G(x -
G(x -  ) =
) = 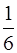 no
no  {G(x) -
{G(x) - 
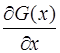 } (11)
} (11)
Поток этого же свойства в отрицательном направлении оси Х равен:
IG(-) = - 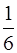 no
no  G(x +
G(x +  ) = -
) = - 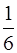 no
no  {G(x) +
{G(x) + 
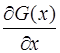 } (12)
} (12)
Появление знака (-) впереди полученного выражения связано с изменением знака скорости молекул, двигающихся по направлению к площадке dS. Суммарный поток G равен сумме обоих потоков
IG = IG(+) + IG(-) = - 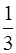 no
no 

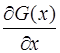 (13)
(13)
Уравнение (13) является обобщенным уравнением процессов переноса.
Учет распределения молекул по скоростям при выводе обобщенного уравнения переноса. В упрощенном выводе, не рассматривалось распределение молекул по скоростям. Считалось, что в среднем все молекулы двигаются с одной и той же скоростью  , поэтому в данном направлении двигается 1/6 от всех молекул. При учете распределения молекул по скоростям оказывается, что поток молекул в направлении выделенной площадки равен не (no
, поэтому в данном направлении двигается 1/6 от всех молекул. При учете распределения молекул по скоростям оказывается, что поток молекул в направлении выделенной площадки равен не (no  )/6, а (no
)/6, а (no  )/4. Кроме того, последнее столкновение перед площадкой молекулы испытывают на расстоянии не
)/4. Кроме того, последнее столкновение перед площадкой молекулы испытывают на расстоянии не 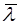 , как мы считали выше, а 2
, как мы считали выше, а 2 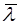 /3. (А.Н. Матвеев. Молекулярная физика, стр. 62, 70 -71). С учетом данных фактов вместо уравнений (11-12) получаем
/3. (А.Н. Матвеев. Молекулярная физика, стр. 62, 70 -71). С учетом данных фактов вместо уравнений (11-12) получаем
IG(+) = 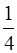 no
no  G(x-
G(x- 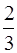
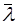 ) =
) = 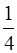 no
no  {G(x) -
{G(x) - 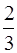

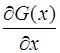 } (
} ( ) IG(-)=-
) IG(-)=- 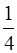 no
no  G(x+
G(x+ 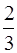
 )= -
)= - 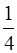 no
no  {G(x)+
{G(x)+ 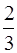
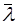
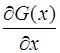 } (
} (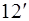 )
)
Суммируя выражения (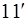 ) и (
) и (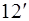 ) легко убедиться, что введенные уточнения не сказались на величине суммарного потока IG(+) + IG(-). Как видим, усложнение вывода не изменило конечного выражения, поэтому возможен и упрощенный вывод соотношения (13).
) легко убедиться, что введенные уточнения не сказались на величине суммарного потока IG(+) + IG(-). Как видим, усложнение вывода не изменило конечного выражения, поэтому возможен и упрощенный вывод соотношения (13).
Из обобщенного уравнения переноса (13) можно получить выражения для потока массы (явление диффузии), энергии (явление теплопроводности) и импульса (вязкое трение).
Явление диффузии – перенос количества молекул.
В этом случае G (x)= n(x)/no . Подставляя данное значение G(x) в уравнение (13), получаем выражение для потока массы:
I n = - 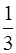 no
no 
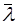
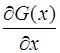 = - D
= - D 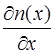 (14)
(14)
Уравнение (14) называется уравнением Фика, где D – есть коэффициент диффузии D= 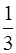

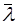 (15)
(15)
Явление теплопроводности – перенос энергии.
В этом случае G (x)= 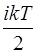 – есть энергия одной молекулы, i – число степеней свободы молекулы.
– есть энергия одной молекулы, i – число степеней свободы молекулы.
G(x)= 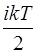 =
= 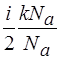 T=
T= 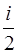
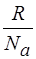 T=
T= 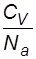 T (16)
T (16)
Подставляя это значение G(x) в уравнение (13), получаем выражение для потока энергии (или тепла)
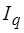 = -
= - 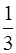 no
no 
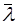
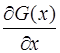 = -
= - 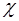
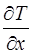 (17)
(17) 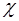 =
= 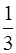 no
no 

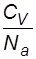 =
= 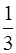 nom
nom 

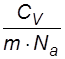 =
= 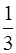
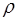


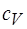 (18)
(18)
Уравнение (17) называется уравнением Фурье, а величина 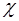 - коэффициентом теплопроводности. В выражении (18)
- коэффициентом теплопроводности. В выражении (18) 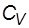 - молярная теплоемкость газа, а
- молярная теплоемкость газа, а 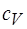 - удельная, m – масса молекулы,
- удельная, m – масса молекулы, 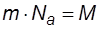 - молярная масса,
- молярная масса, 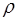 = nom – плотность газа.
= nom – плотность газа.
Явление вязкого трения – перенос импульс а.
В этом случае G (x)= m 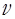 – есть импульс одной молекулы,
– есть импульс одной молекулы, 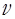 – ее скорость. Подставляя данное значение G(x) в уравнение (13), получаем выражение для потока импульса
– ее скорость. Подставляя данное значение G(x) в уравнение (13), получаем выражение для потока импульса
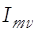 = -
= - 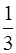 no
no 

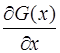 = -
= - 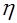
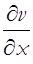 (19)
(19)
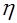 =
= 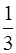 no
no 
 m =
m = 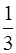
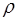

 (20)
(20)
Величина 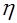 - есть коэффициент динамической вязкости. Уравнение (20) впервые получено Дж. Максвеллом в 1860 году.
- есть коэффициент динамической вязкости. Уравнение (20) впервые получено Дж. Максвеллом в 1860 году.
 2015-03-07
2015-03-07 1984
1984






