Принцип размерного квантования. Понятие о плотности состояний в низкоразмерных системах

III. Транспортные свойства сопряжённых систем.

Квантовые размерные эффекты и условия их наблюдения

Принцип размерного квантования. Понятие о плотности состояний в низкоразмерных системах.

Весь комплекс явлений, обычно понимаемый под словом электронные свойства низкоразмерных электронных систем, имеет в своей основе один фундаментальный физический факт – изменение энергетического спектра электронов и дырок в структурах с очень малыми размерами. Изменение физических и химических свойств частиц вещества, происходящих с изменением геометрических размеров частиц вещества, приводит к необходимости рассмотрения понятия ультрадисперсности. В общем случае под дисперсностью понимают степень раздробленности вещества на частицы. Чем меньше размер отдельной частицы, тем выше дисперсность. Большинство веществ окружающего нас мира существуют в виде дисперсных систем, которые по степени дисперсности частиц вещества можно разделить на три основные группы – грубодисперсные, высокодисперсные и ультрадисперсные. Ещё в XIX веке М. Фарадей впервые создал коллоидную суспензию золота, состоящую из крошечных частиц этого металла. При этом им было обнаружено, что цвет суспензии менялся на фиолетовый. Это в свою очередь свидетельствовало об изменении отражающих свойств суспензии при уменьшении размеров частиц. Повышенный интерес учёных к такого рода системам объясняется, прежде всего, тем, что уменьшение дисперсности частиц какого-либо вещества может приводить к заметным изменениям их свойств. Например, известно, что частицы серебра оказывают антибактериальное действие, однако только в последнее время стало известно, что в виде наночастиц активность серебра повышается в тысячи раз. Такие ультрадисперсные частицы как фуллерены и нанотрубки, своими удивительными свойствами также подтверждают тот факт, что многие вещества в наноформе не ведут себя таким же самым образом, как в своём привычном для нас виде. Особое внимание заслуживают так называемые ультрадисперсные системы, состоящие из частиц нанометрового масштаба. Вследствие размерного эффекта материалам в ультрадисперсном состоянии могут быть присущи уникальные сочетания химических, электрических, магнитных, тепловых, механических, сорбционных, радиопоглощающих и других свойств, не встречающихся в массивных телах. В отдельных малых частицах реализуются разнообразные размерные эффекты, наблюдается качественное изменение спектров элементарных возбуждений, чувствительных как к изменению симметрии, так и к наличию границ. Этим вызываются определённые аномалии в поведении электронов, фононов, плазмонов, магнонов и других элементарных возбуждений. Возможно, возникновение корреляций электронных состояний одновременно во многих частицах, что, по-видимому, важно для понимания сверхпроводящих свойств ультрадисперсных сред. Полвека тому назад Р. Фейнман для своей лекции о проблемах миниатюризации выбрал парадоксальное название «Внизу полным-полно места». Сегодня становится очевидным, какое значение имеют или будут иметь в будущем некоторые положения лекции Р. Фейнмана, прочитанной накануне 1960 года в Калифорнийском технологическом институте на Рождественском обеде Американского физического общества: «Речь идет о проблеме контроля и управления строением вещества в интервале очень малых размеров. Внизу (то есть «внизу или внутри пространства», если угодно) располагается поразительно сложный мир малых форм, и когда-нибудь (году, например, в 2000-м) люди будут удивляться тому, что до 1960 года никто не относился серьезно к исследованию этого мира... Поскольку для записи одного бита информации нам необходимо примерно 100 атомов, вся заботливо собранная человечеством книжная информация может быть «записана» в кубике металла с размером грани около 1/200 дюйма, представляющем крошечную, едва различимую человеческим глазом пылинку. Как видите, в глубинах пространства, внизу, полным-полно места и возможностей...

По мере уменьшения размеров мы будем постоянно сталкиваться с очень необычными физическими явлениями. Всё, с чем приходится встречаться в жизни, зависит от масштабных факторов... Внизу мы будем постоянно наблюдать новые закономерности и эффекты, предполагающие новые варианты использования».

В 2000 г. коллектив американских исследователей издал книгу «Нанотехнология в ближайшем десятилетии», целью которой являлось ознакомление американской общественности с состоянием нанотехнологических исследований к началу 1999 г. Нанонауку можно определить как совокупность знаний о свойствах вещества в нанометровом диапазоне. Нанотехнологию – как умение целенаправленно создавать объекты с заранее заданными составом, размерами и структурой в диапазоне приблизительно 1—100 нм. В последнее время было разработано достаточно большое число методов получения ультрадисперсных систем, позволяющих весьма тонко регулировать размеры частиц, их форму и строение. Эти методы могут быть разделены на две группы: диспергационные (механическое, термическое, электрическое измельчение или распыление макроскопической фазы) и конденсационные (химическая или физическая конденсация). Примерами ультрадисперсных систем являются нанопорошки, множество коллоидных систем, микроэмульсии и т.п. Размерные границы ультрадисперсности строго не определены, и в разных областях знания в это понятие вкладывается несколько различное количественное содержание. Итак, выше было дано понятие ультрадисперсности и показано, что с уменьшением размера частиц вещества его физические и химические свойства могут существенно меняться. Это происходит из-за того, что ход физических процессов зависит не только от свойств самого вещества, но и от геометрии той области пространства, в которой они протекают, то есть от размеров этой области. Для наглядной иллюстрации этой идеи следует обратиться к следующей аналогии: представим, что в узком переулке нужно развернуться какому-то транспортному средству. Очевидно, что мотоциклисту это будет сделать гораздо легче, чем водителю тяжёлого грузовика. Размерные эффекты в твёрдых телах – это явления, наблюдающиеся в условиях, когда геометрические размеры объекта сравнимы с длиной свободного пробега носителей заряда (электронов и дырок) или длиной волны де Бройля, определяющих протекание физических процессов. В зависимости от размеров исследуемого образца различают классические и квантовые размерные эффекты, которые могут влиять практически на любые свойства вещества. Очевидно, что для объектов нанометрового масштаба, где размеры частиц сравнимы с де Бройлевской длиной волны электрона, характерны именно квантовые размерные эффекты, определяющие такие свойства вещества, как теплоёмкость, электропроводность, некоторые оптические свойства. Самым ярким представителем квантовых размерных эффектов является туннельный эффект – чисто квантовое явление, сыгравшее важную роль в развитии современной электронике и приборостроении. Феномен туннелирования открыл в 1928 г. наш соотечественник Г. А. Гамов, впервые получив решения уравнения Шрёдингера, описывающие возможность преодоления частицей потенциального барьера, даже если её энергия меньше высоты барьера. Найденное решение объясняло многие экспериментальные данные и позволило понять большой круг явлений, происходящих при 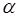- распаде ядра. Многие считают, что за грандиозность результатов его работ, ставших основополагающими для многих наук, Г.А. Гамов должен был быть удостоен нескольких Нобелевских премий. Лишь спустя тридцать лет после открытия Г. А. Гамова появились первые приборы на основе туннельного эффекта – туннельные диоды, транзисторы, датчики, термометры для измерения сверхнизких температур, и, наконец, сканирующие туннельные микроскопы, положившие начало современным исследованиям наноструктур. Идею размерного квантования достаточно удобным является показать, прибегая к элементарным модельным представлениям – модели одномерного потенциального ящика и далее для случая молекул линейных полиенов – модели свободного электрона (МСЭ). То обстоятельство, что в обычных условиях носители заряда сосредоточены в плёнке и не выходят из неё в окружающую среду, означает, что материал плёнки (например, полупроводник) представляет собой потенциальную яму для электронов глубиной, равной работе выхода 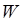, и шириной 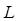. Согласно законам квантовой механики, энергия электронов в такой яме квантуется, т.е. может принимать лишь некоторые дискретные значения 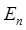, где 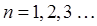принимая, таким образом, лишь целочисленные значения. Эти дискретные значения энергии называют уровнями размерного квантования. Типичные значения работы выхода в большинстве твёрдых тел имеют величину порядка 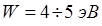, на несколько порядков превышающую характерную тепловую энергию носителей заряда 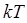, равную при комнатной температуре 0,026 эВ, поэтому потенциальную яму можно в общем случае считать бесконечно глубокой. Другим необходимым условием, позволяющим считать яму бесконечно глубокой, является малость значений 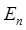, по сравнению с её действительной глубиной 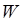. Это условие, которое для нижних уровней можно записать в виде:

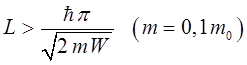
соответствует толщинам плёнки порядка нескольких межатомных расстояний. Во всех реальных структурах это условие соблюдается. Для лучшего понимания основной идеи размерного квантования в низкоразмерных электронных системах, рассмотрим некоторую плёнку, занимающую область .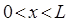

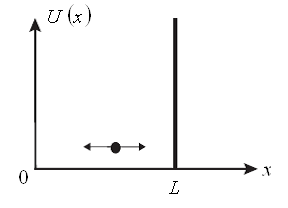
Рис.2. Одномерное движение частицы в одномерном потенциальном ящике

Пусть частица в такой плёнке свободно движется в жёстких пределах, например в интервале длиной 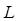, тогда соответственно:

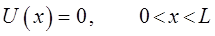
это означает, что в концевых точках интервала, потенциальная энергия становится бесконечной, т.е.

Это и есть случай одномерного потенциального ящика. При таких граничных условиях частица с конечной энергией, не может вырваться за пределы данного интервала 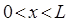, тогда уравнение Шрёдингера:

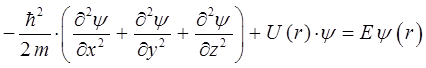
для рассматриваемого одномерного случая при 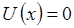, преобразуется к виду:

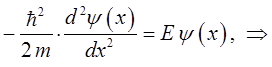
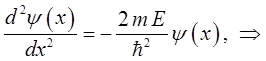
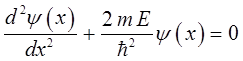
Последнее выражение аналогично полученному уже ранее уравнению:

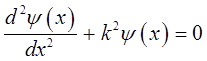
очевидно, что:

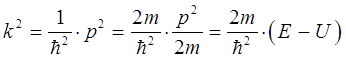
которое при граничном условии вида 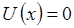, сводится к уравнению:

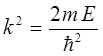
Действительно, учитывая уравнения, связывающие волновой вектор с импульсом микрочастицы:

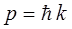
и её кинетической энергией:

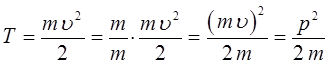
и таким образом:

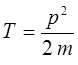
откуда:

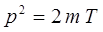
тогда:

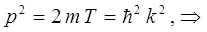
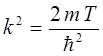
поскольку:

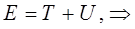
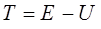
имеем соответственно:

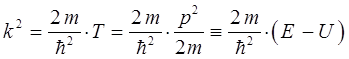
Поскольку при 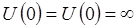, то вероятность нахождения электрона 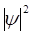, а, следовательно, и 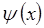вне указанного интервала, начиная с концов 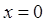и 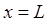, исчезает. Исходя из этих соображений, получаем краевые условия вида:

Для рассматриваемой задачи, решение уравнения Шрёдингера:

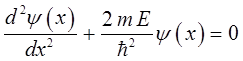
приводит к суперпозиции сопряжённых друг другу решений вида:

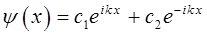
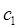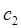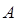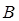Поскольку здесь коэффициенты и представляют собой амплитуды соответствующих стоячих волн и , тогда соответствующие решения волнового уравнения можно будет переписать в виде:

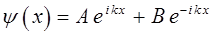
В точках пространства 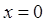и 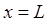, уравнение Шрёдингера имеет тривиальное решение 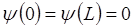. Это и есть дополнительные (граничные или краевые) условия для нахождения постоянных 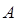и 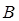. Из первого граничного условия 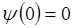находим соответственно:

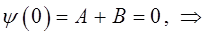
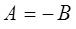
тогда:

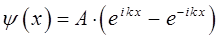
на основании формул Эйлера для показательной функции:

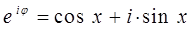
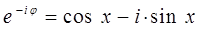
и эквивалентных им формул вида:

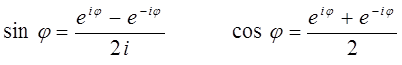
получаем для волновой функции тригонометрическое выражение вида:

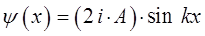
Заменив коэффициент 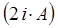в полученном выше выражении на общий нормировочный множитель , приходим к выражению вида:

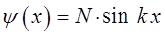
Для уточнения структуры волновой функции, подставим в последнее выражение значение координаты 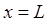. Учитывая второе граничное условие в точке 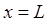и соответственно 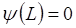, получим соответственно:

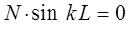
Полученное нами тригонометрическое уравнение имеет решение при условии, когда:

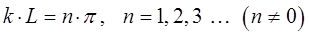
откуда следует, что:

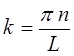
Условие вида 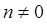принципиально, поскольку при 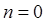волновая функция 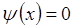не имеет физического смысла – частицы нигде нет (здесь 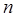- квантовое число). Таким образом, в потенциальной яме волновой вектор 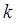, а, следовательно, и импульс 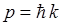принимает дискретный ряд значений:

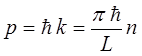
поскольку как было показано выше:

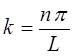
тогда волновая функция 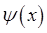приобретает вид:

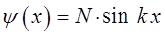
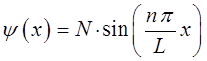
Нормировочный множитель найдём из условия нормировки (общий случай):

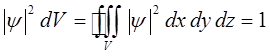
или для частного случая, в рамках рассматриваемой модельной задачи будем иметь соответственно:

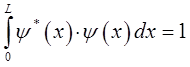
подставляя в подынтегральное выражение значение волновой функции:

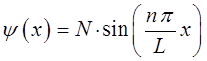
будем иметь соответственно:

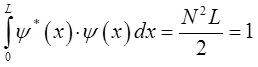
действительно:

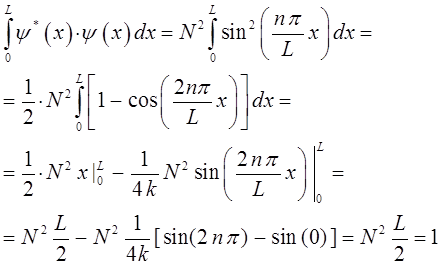
откуда следует, что:

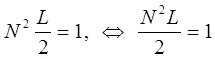
откуда:

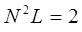
и

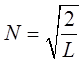
На основании проделанных выкладок, структура волновой функции частицы в потенциальной яме с бесконечно высокими стенками может быть уточнена и будет иметь вид:

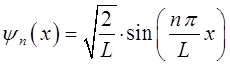
Графики волновых функций 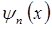и плотности вероятности частиц 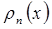принято изображать на диаграмме энергетических уровней, которые, в свою очередь, совмещают с графиком потенциальной энергии. Из представлений модели прямоугольного потенциального ящика непосредственно следует такое важное понятие как узловая точка – такая точка пространства, при переходе через которую волновая функция меняет свой знак на противоположный. Это в свою очередь является принципиальным, поскольку наличие или отсутствие последней определяет существование орбитального квантового числа 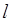. Так, с увеличением главного квантового числа 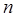, число узловых точек также увеличивается и принимает значение порядка 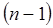. Чтобы найти узловые точки, волновую функцию приравнивают нулю:

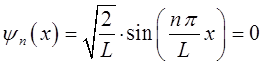
принимая, что:

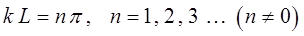
здесь:

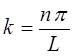
откуда следует соответственно, что:

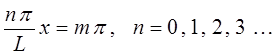
или после соответствующих преобразований имеем:

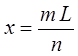
Используя полученное выше выражение, рассчитает количество узловых точек для каждого 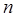. При этом ограничимся случаем 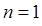, 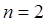и 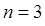. Для нижнего энергетического уровня с 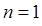, значения 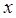равны: 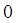, , 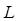, 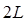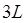… Однако по условию задачи частица, движущаяся в жёстких пределах 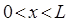, не может находиться за границей указанного интервала. Так, при 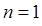волновая функция 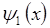узлов не имеет. Для следующего энергетического уровня с 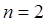, значения 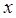равны соответственно: 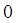, 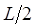и 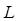. Однако узловой точкой здесь является точка 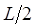. И наконец, для уровня с квантовым числом 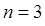получаем: 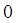, , 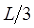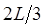и 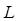. Здесь, для частицы, движущейся в пределах 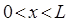, узловыми являются две точки - 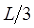и . 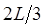В общем случае для волновой функции 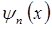число узлов будет очевидно равно 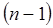, что хорошо видно из приведенных ниже схем.

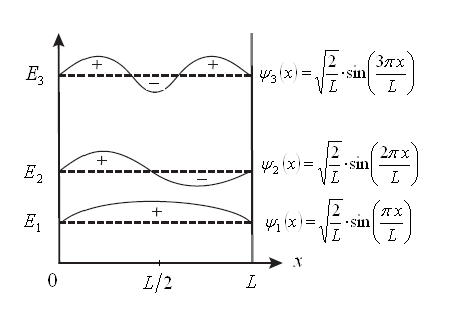
Рис.3. Волновые функции частицы в одномерном потенциальном ящике

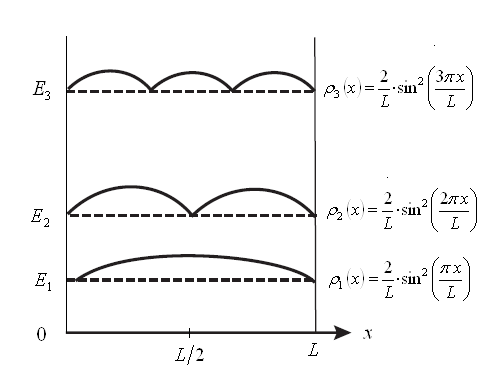
Рис.4. Плотности вероятности для частицы в одномерном потенциальном ящике

Найдём энергию частицы в потенциальном ящике. Так, частица свободно движется в пределах интервала 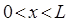, уравнение Шредингера, описывающее такое движение частицы, очевидно, будет иметь вид:

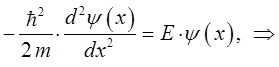
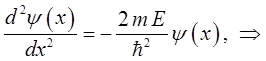
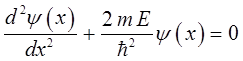
очевидно, данное уравнение будет иметь гармонические решения вида:

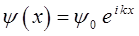
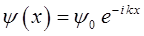
здесь 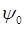представляет собой нормировочный множитель. Нетрудно убедиться, что данные решения действительно удовлетворяют уравнению:

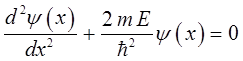
для этого вычислим первую и вторую производные от данных функций:

или в общем виде:

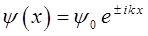
имеем соответственно:

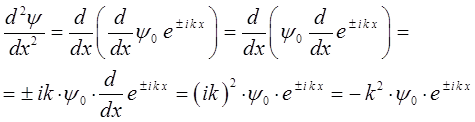
и далее:

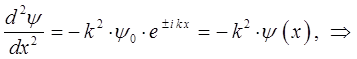
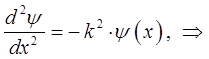
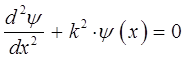
приравнивая между собой эквивалентные формы уравнения Шрёдингера для рассматриваемой одномерной задачи:

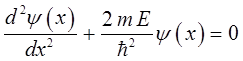
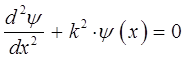
после преобразования последнего уравнения к виду:

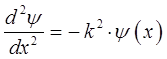
будем иметь соответственно:

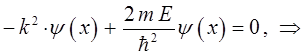
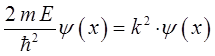
или что то же самое:

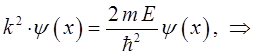
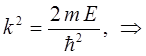
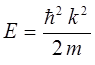
учитывая, что:

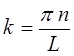
и соответственно:

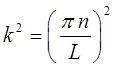
будем иметь:

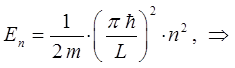
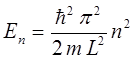
Поскольку свободное движение частицы совершается строго в пределах интервала 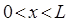, то очевидно, что выражение для энергии частицы в потенциальном ящике будет функцией параметра (квантового числа) 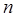, тогда соответственно:

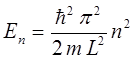
при :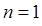

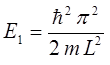
при :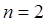

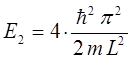
при :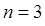

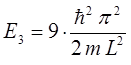
при :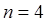

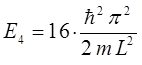
при :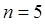

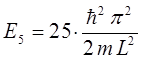
и в общем случае, при :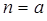

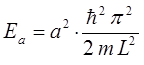
имеем:

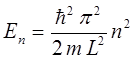
С учётом приведенных выше соображений, общее выражение для энергии частицы в одномерном потенциальном ящике приобретёт вид:

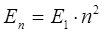
тогда значения энергий частицы в потенциальном ящике образуют ряд:

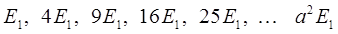
это и означает, что энергия частицы в одномерном потенциальном ящике дискретная, квантованная величина. На основании полученных данных, легко построить диаграмму энергетических уровней частицы в одномерном потенциальном ящике и получить значения энергии перехода между двумя соседними уровнями. Действительно, из выражения вида:

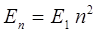
достаточно просто получить общее соотношение для энергии перехода между любыми двумя уровнями с квантовыми числам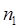и и :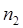

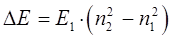
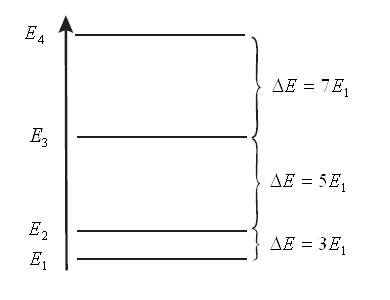
Рис.5. Диаграмма энергетических уровней частицы находящейся в одномерном потенциальном ящике

Необходимо отметить, что так называемые допустимые дискретные значения энергии частицы находящейся в прямоугольном потенциальном ящике можно также получить на основании полученных нами уже ранее выражений. Так, имеем:

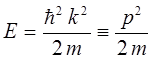
где

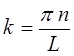
и соответственно:

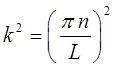
а также:

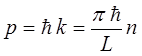
Сопоставляя между собой данные уравнения, приходим к выражению:

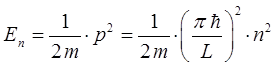
учитывая, что:

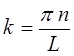
и соответственно:

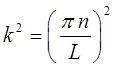
будем иметь:

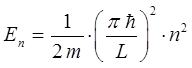
или что тоже самое:

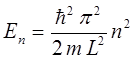
В этой задаче прослеживается характерная особенность квантово-механического подхода – квантование возникает как результат наложения на решение дифференциального уравнения определённых краевых условий. Как это следует из последнего выражения:

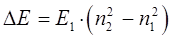
расстояние между энергетическими уровнями будет зависеть от массы частицы 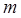и ширины ящика 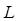. Очевидно, чем больше будет масса частицы и ширина ящика, тем больше будет величина 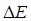. Тогда при условии 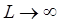энергетические уровни будут сближаться, а наименьшее значение энергии будет стремиться к нулю 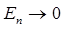. Это будет в свою очередь означать, что энергия теряет квантовый характер и становится непрерывной величиной, что приводит к исчезновению квантования. Итак, в рассматриваемой модельной задаче прослеживается одна характерная особенность квантово-механического подхода – квантование возникает как результат наложения на решение дифференциального уравнения определённых краевых условий. При этом полная энергия для частицы в потенциальной яме может иметь лишь дискретные, кратные значению 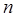энергии, т.е. квантуется. При этом что интересно, дискретность возникает как следствие решения уравнения Шрёдингера с учётом граничных (краевых) условий, т.е. отпадает необходимость введения каких либо постулатов, касающихся квантования физических величин, как это было например в случае теории Бора.