Одним из наиболее важных способов численного решения уравнений является метод итерации. Сущность этого метода заключается в следующем. Пусть дано уравнение (1) 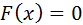 , где
, где 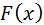 - непрерывная функция, и требуется определить его вещественные корни. Заменим уравнение (1) равносильным уравнением
- непрерывная функция, и требуется определить его вещественные корни. Заменим уравнение (1) равносильным уравнением
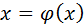 (5)
(5)
Выберем каким-либо способом грубо приближенное значение корня 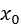 и подставим его в правую часть уравнения (5). Тогда получим некоторое число
и подставим его в правую часть уравнения (5). Тогда получим некоторое число
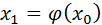 (6)
(6)
Подставляя теперь в правую часть равенства (6) вместе 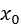 число
число 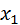 , получим новое число
, получим новое число 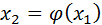 . Повторяя этот процесс, будем иметь последовательность чисел
. Повторяя этот процесс, будем иметь последовательность чисел
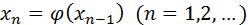 (7)
(7)
Если эта последовательность – сходящаяся, т.е. существует предел 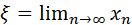 , то, переходя к пределу в равенстве (7) и предполагая функцию
, то, переходя к пределу в равенстве (7) и предполагая функцию 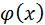 непрерывной, найдем:
непрерывной, найдем:
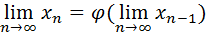
или 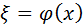 (8)
(8)
Таким образом, предел 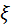 является корнем уравнения (5) и может быть вычислен по формуле (7) с любой степенью точности.
является корнем уравнения (5) и может быть вычислен по формуле (7) с любой степенью точности.
Условие сходимости итерационного процесса определяется теоремой о достаточном условии сходимости итерационного процесса.
Теорема: Пусть уравнение 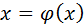 имеет единственный корень на отрезке
имеет единственный корень на отрезке 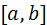 и выполнены условия:
и выполнены условия:
1. 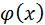 определена и дифференцируема на отрезке
определена и дифференцируема на отрезке 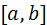 .
.
2. 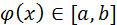 для всех
для всех 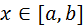 .
.
3. Существует такое вещественное 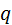 , что
, что 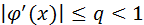 для всех
для всех 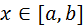 .
.
Тогда итерационная последовательность 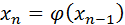
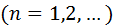 сходится при любом начальном приближении
сходится при любом начальном приближении 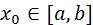 .
.
Замечание: Условия теоремы не являются необходимыми. Это означает, что итерационная последовательность может оказаться сходящейся и при невыполнении этих условий.
ПРЕОБРАЗОВАНИЕ УРАВНЕНИЯ
К ИТЕРАЦИОННОМУ ВИДУ
Уравнение 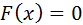 преобразуется к виду, пригодному для итерационного процесса, следующим преобразованием
преобразуется к виду, пригодному для итерационного процесса, следующим преобразованием
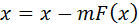 ,
,
где m – отличная от нуля константа.
В этом случае
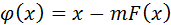 (9)
(9)
Функция 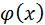 должна удовлетворять условиям теоремы. Дифференцируя (9), получим
должна удовлетворять условиям теоремы. Дифференцируя (9), получим
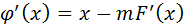 (10)
(10)
Для выполнения условия 3 теоремы достаточно подобрать m так, чтобы для всех 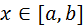 выполнялось
выполнялось 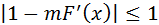
 2015-03-22
2015-03-22 400
400








